Longitude

Longitude (/ˈlɒndʒɪtjuːd/, AU and UK also /ˈlɒŋɡɪ-/),[1][2] is a geographic coordinate that specifies the east–west position of a point on the Earth's surface, or the surface of a celestial body. It is an angular measurement, usually expressed in degrees and denoted by the Greek letter lambda (λ). Meridians (lines running from pole to pole) connect points with the same longitude. The prime meridian, which passes near the Royal Observatory, Greenwich, England, is defined as 0° longitude by convention. Positive longitudes are east of the prime meridian, and negative ones are west.

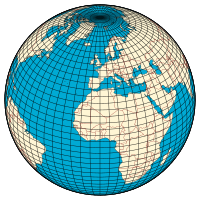
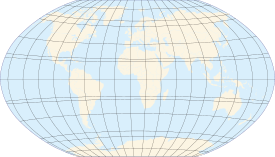For Dava Sobel's book about John Harrison, see Longitude (book). For the adaptation of Sobel's book, see Longitude (TV series). For other uses, see Longitude (disambiguation).
A graticule on the Earth as a sphere or an ellipsoid. The lines from pole to pole are lines of constant longitude, or meridians. The circles parallel to the Equator are circles of constant latitude, or parallels. The graticule shows the latitude and longitude of points on the surface. In this example, meridians are spaced at 6° intervals and parallels at 4° intervals.
Longitude (λ)
Lines of longitude appear vertical with varying curvature in this projection, but are actually halves of great ellipses, with identical radii at a given latitude.
Latitude (φ)
Lines of latitude appear horizontal with varying curvature in this projection; but are actually circular with different radii. All locations with a given latitude are collectively referred to as a circle of latitude.
The equator divides the planet into a Northern Hemisphere and a Southern Hemisphere, and has a latitude of 0°.
Geodesy

A location's north–south position along a meridian is given by its latitude, which is approximately the angle between the local vertical and the equatorial plane.

Longitude is generally given using the geometrical or astronomical vertical. This can differ slightly from the gravitational vertical because of small variations in Earth's gravitational field.

History
Main article: History of longitude
Amerigo Vespucci's observations: the origins of the "lunar distance method"

The measurement of longitude is important both to cartography and for ocean navigation. Mariners and explorers for most of history struggled to determine longitude. Finding a method of determining longitude took centuries and required the effort of some of the greatest scientific minds.

Latitude was calculated by observing with quadrant or astrolabe the altitude of the sun or of charted stars above the horizon, but longitude is harder.

Christopher Columbus in 1494 exploited a relatively rare, predicted, astronomical event (a lunar eclipse) to estimate his longitude while at Saona Island (now in the Dominican Republic): "El año de mil cuatrocientos noventa y cuatro estando yo en la isla Saona, que es al cabo Oriental de la isla Española, hubo eclipsis de la luna à catorce de Setiembre, y se fallò que habia diferencia de alli al Càbo de S. Vicente en Portugal cinco horas y mas de media"[3] Translation: "In the year 1494, when I was in Saona Island, which stands at the eastern tip of Española island [i.e. Hispaniola], there was a lunar eclipse on September the 14th, and we noticed that there was a difference of more than five hours and a half between there [Saona] and Cape S.Vincente, in Portugal" [of course meaning he had an almanac, foreseeing the lunar eclipse timing when seen from Portugal]. This has obvious implications on Columbus's being finally aware (and the first to prove) that - contrary to his wishes and expectations - he had not reached 'the Indies', after all. Had he actually been there, in fact, he would have been roughly at the antipodes of Europe (see Behaims' globe), and not just 5.5 hours west of it.

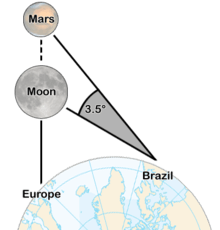
Amerigo Vespucci appears to be the first European to offer a solution not depending on rare astronomical occurrences, after devoting a great deal of time and energy studying the problem during his sojourns in the New World:

As to longitude, I declare that I found so much difficulty in determining it that I was put to great pains to ascertain the east-west distance I had covered. The final result of my labours was that I found nothing better to do than to watch for and take observations at night of the conjunction of one planet with another, and especially of the conjunction of the moon with the other planets, because the moon is swifter in her course than any other planet. I compared my observations with an almanac. After I had made experiments many nights, one night, the twenty-third of August 1499, there was a conjunction of the moon with Mars, which according to the almanac was to occur at midnight or a half hour before. I found that...at midnight Mars's position was three and a half degrees to the east.[4]

John Harrison solved the greatest problem of his day.[5]

That said, Vespucci's writings appear to have been corrupted. (see reference) By comparing the timing of the observed positions of the moon and Mars with the expected timing of their occurrence when seen from Europe (Florence or Nuremberg), Vespucci would actually have been able to deduce his longitude (measured in hours). However, for (t)his method to provide usable results, three conditions should be satisfied: First, it requires waiting for a specific expected astronomical event to occur (in this case, Mars passing through the same right ascension as the moon), and its occurrence to be accurately timed in an astronomical almanac. Second, one needs to know the precise local time, something difficult to ascertain for Vespucci, when travelling especially. Third, it requires a stable viewing platform, rendering the technique useless on the rolling deck of a ship at sea. See Lunar distance (navigation). Due to none of such conditions being fulfilled when Vespucci took his measures (except for the third one, if he was on the ground), there was no possibility for him to accurately esteem his longitude. Notheless he must be credited with having envisioned a correct method to measure longitude (in hours, easily transformed into degrees: 1 hour = 15 degrees). Such a method was to be named the "Lunar distance method" and it became usable by mariners much later, when lunar positions started to be known and published in an accurate enough Almanac: the one issued by astronomer Nevil Maskelyne (1732-1811).see reference

In 1612 Galileo Galilei demonstrated that with sufficiently accurate knowledge of the orbits of the moons of Jupiter one could use their positions as a universal clock and this would make possible the determination of longitude, but the method he devised was impracticable for navigators on ships because of their instability.[6] In 1714 the British government passed the Longitude Act which offered large financial rewards to the first person to demonstrate a practical method for determining the longitude of a ship at sea. These rewards motivated many to search for a solution.

Drawing of Earth with longitudes but without latitudes.

John Harrison, a self-educated English clockmaker, invented the marine chronometer, the key piece in solving the problem of accurately establishing longitude at sea, thus revolutionising and extending the possibility of safe long distance sea travel.[5] A French expedition under Charles-François-César Le Tellier de Montmirail performed the first measurement of longitude aboard Aurore in 1767.[7] Though the Board of Longitude rewarded John Harrison for his marine chronometer in 1773, chronometers remained very expensive and the lunar distance method continued to be used for decades. Finally, the combination of the availability of marine chronometers and wireless telegraph time signals put an end to the use of lunars in the 20th century.

Unlike latitude, which has the equator as a natural starting position, there is no natural starting position for longitude. Therefore, a reference meridian had to be chosen. It was a popular practice to use a nation's capital as the starting point, but other locations were also used. While British cartographers had long used the Greenwich meridian in London, other references were used elsewhere, including El Hierro, Rome, Copenhagen, Jerusalem, Saint Petersburg, Pisa, Paris (see the article Paris meridian), Philadelphia, and Washington D.C. In 1884 the International Meridian Conference adopted the Greenwich meridian as the universal Prime Meridian or zero point of longitude.[8]

Noting and calculating longitude

Longitude is given as an angular measurement ranging from 0° at the Prime Meridian to +180° eastward and −180° westward. The Greek letter λ (lambda),[9][10] is used to denote the location of a place on Earth east or west of the Prime Meridian.

Each degree of longitude is sub-divided into 60 minutes, each of which is divided into 60 seconds. A longitude is thus specified in sexagesimal notation as 23° 27′ 30″ E. For higher precision, the seconds are specified with a decimal fraction. An alternative representation uses degrees and minutes, where parts of a minute are expressed in decimal notation with a fraction, thus: 23° 27.5′ E. Degrees may also be expressed as a decimal fraction: 23.45833° E. For calculations, the angular measure may be converted to radians, so longitude may also be expressed in this manner as a signed fraction of π (pi), or an unsigned fraction of 2π.

For calculations, the West/East suffix is replaced by a negative sign in the western hemisphere. The preferred convention—that East is positive—is consistent with a right-handed Cartesian coordinate system, with the North Pole up. A specific longitude may then be combined with a specific latitude (usually positive in the northern hemisphere) to give a precise position on the Earth's surface. Confusingly, the convention of negative for East is also sometimes seen, most commonly in the United States; the Earth System Research Laboratory notes that, while it differs from the international standard, it "make(s) coordinate entry less awkward" for applications confined to the Western Hemisphere.[11]

There is no other physical principle determining longitude directly but with time. Longitude at a point may be determined by calculating the time difference between that at its location and Coordinated Universal Time (UTC). Since there are 24 hours in a day and 360 degrees in a circle, the sun moves across the sky at a rate of 15 degrees per hour (360° ÷ 24 hours = 15° per hour). So if the time zone a person is in is three hours ahead of UTC then that person is near 45° longitude (3 hours × 15° per hour = 45°). The word near is used because the point might not be at the center of the time zone; also the time zones are defined politically, so their centers and boundaries often do not lie on meridians at multiples of 15°. In order to perform this calculation, however, a person needs to have a chronometer (watch) set to UTC and needs to determine local time by solar or astronomical observation. The details are more complex than described here: see the articles on Universal Time and on the equation of time for more details.

Singularity and discontinuity of longitude

Note that the longitude is singular at the Poles and calculations that are sufficiently accurate for other positions may be inaccurate at or near the Poles. Also the discontinuity at the ±180° meridian must be handled with care in calculations. An example is a calculation of east displacement by subtracting two longitudes, which gives the wrong answer if the two positions are on either side of this meridian. To avoid these complexities, consider replacing latitude and longitude with another horizontal position representation in calculation.

Plate movement and longitude

The Earth's tectonic plates move relative to one another in different directions at speeds on the order of 50 to 100 mm (2.0 to 3.9 in) per year.[12] So points on the Earth's surface on different plates are always in motion relative to one another. For example, the longitudinal difference between a point on the Equator in Uganda, on the African Plate, and a point on the Equator in Ecuador, on the South American Plate, is increasing by about 0.0014 arcseconds per year. These tectonic movements likewise affect latitude.

If a global reference frame (such as WGS84, for example) is used, the longitude of a place on the surface will change from year to year. To minimize this change, when dealing just with points on a single plate, a different reference frame can be used, whose coordinates are fixed to a particular plate, such as "NAD83" for North America or "ETRS89" for Europe.

Length of a degree of longitude

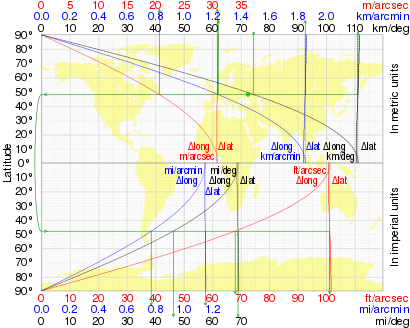
The length of a degree of longitude (east-west distance) depends only on the radius of a circle of latitude. For a sphere of radius a that radius at latitude φ is a cos φ, and the length of a one-degree (or π/180 radian) arc along a circle of latitude is

φΔ1
lat		Δ1
long
0°110.574 km111.320 km
15°110.649 km107.551 km
30°110.852 km96.486 km
45°111.133 km78.847 km
60°111.412 km55.800 km
75°111.618 km28.902 km
90°111.694 km0.000 km
Length of one degree (black), minute (blue) and second (red) of latitude and longitude in metric (upper half) and imperial units (lower half) at a given latitude (vertical axis) in WGS84. For example, the green arrows show that Donetsk (green circle) at 48°N has a Δlong of 74.63 km/° (1.244 km/min, 20.73 m/sec etc) and a Δlat of 111.2 km/° (1.853 km/min, 30.89 m/sec etc).

When the Earth is modelled by an ellipsoid this arc length becomes[13][14]

where e, the eccentricity of the ellipsoid, is related to the major and minor axes (the equatorial and polar radii respectively) by

An alternative formula is

; here is the so-called parametric or reduced latitude.

Cos φ decreases from 1 at the equator to 0 at the poles, which measures how circles of latitude shrink from the equator to a point at the pole, so the length of a degree of longitude decreases likewise. This contrasts with the small (1%) increase in the length of a degree of latitude (north-south distance), equator to pole. The table shows both for the WGS84 ellipsoid with a = 6378137.0 m and b = 6356752.3142 m. Note that the distance between two points 1 degree apart on the same circle of latitude, measured along that circle of latitude, is slightly more than the shortest (geodesic) distance between those points (unless on the equator, where these are equal); the difference is less than 0.6 m (2 ft).

A geographical mile is defined to be the length of one minute of arc along the equator (one equatorial minute of longitude), therefore a degree of longitude along the equator is exactly 60 geographical miles or 111.3 kilometers, as there are 60 minutes in a degree. The length of 1 minute of longitude along the equator is 1 geographical mile or 1.855 km or 1.153 miles, while the length of 1 second of it is 0.016 geographical mile or 30.916 m or 101.43 feet.

Longitude on bodies other than Earth

Planetary co-ordinate systems are defined relative to their mean axis of rotation and various definitions of longitude depending on the body. The longitude systems of most of those bodies with observable rigid surfaces have been defined by references to a surface feature such as a crater. The north pole is that pole of rotation that lies on the north side of the invariable plane of the solar system (near the ecliptic). The location of the prime meridian as well as the position of the body's north pole on the celestial sphere may vary with time due to precession of the axis of rotation of the planet (or satellite). If the position angle of the body's prime meridian increases with time, the body has a direct (or prograde) rotation; otherwise the rotation is said to be retrograde.

In the absence of other information, the axis of rotation is assumed to be normal to the mean orbital plane; Mercury and most of the satellites are in this category. For many of the satellites, it is assumed that the rotation rate is equal to the mean orbital period. In the case of the giant planets, since their surface features are constantly changing and moving at various rates, the rotation of their magnetic fields is used as a reference instead. In the case of the Sun, even this criterion fails (because its magnetosphere is very complex and does not really rotate in a steady fashion), and an agreed-upon value for the rotation of its equator is used instead.

For planetographic longitude, west longitudes (i.e., longitudes measured positively to the west) are used when the rotation is prograde, and east longitudes (i.e., longitudes measured positively to the east) when the rotation is retrograde. In simpler terms, imagine a distant, non-orbiting observer viewing a planet as it rotates. Also suppose that this observer is within the plane of the planet's equator. A point on the Equator that passes directly in front of this observer later in time has a higher planetographic longitude than a point that did so earlier in time.

However, planetocentric longitude is always measured positively to the east, regardless of which way the planet rotates. East is defined as the counter-clockwise direction around the planet, as seen from above its north pole, and the north pole is whichever pole more closely aligns with the Earth's north pole. Longitudes traditionally have been written using "E" or "W" instead of "+" or "−" to indicate this polarity. For example, −91°, 91°W, +269° and 269°E all mean the same thing.

The reference surfaces for some planets (such as Earth and Mars) are ellipsoids of revolution for which the equatorial radius is larger than the polar radius, such that they are oblate spheroids. Smaller bodies (Io, Mimas, etc.) tend to be better approximated by triaxial ellipsoids; however, triaxial ellipsoids would render many computations more complicated, especially those related to map projections. Many projections would lose their elegant and popular properties. For this reason spherical reference surfaces are frequently used in mapping programs.

The modern standard for maps of Mars (since about 2002) is to use planetocentric coordinates. Guided by the works of historical astronomers, Merton E. Davies established the meridian of Mars at Airy-0 crater.[15][16] For Mercury, the only other planet with a solid surface visible from Earth, a thermocentric coordinate is used: the prime meridian runs through the point on the equator where the planet is hottest (due to the planet's rotation and orbit, the sun briefly retrogrades at noon at this point during perihelion, giving it more sun). By convention, this meridian is defined as exactly twenty degrees of longitude east of Hun Kal.[17][18][19]

Tidally-locked bodies have a natural reference longitude passing through the point nearest to their parent body: 0° the center of the primary-facing hemisphere, 90° the center of the leading hemisphere, 180° the center of the anti-primary hemisphere, and 270° the center of the trailing hemisphere.[20] However, libration due to non-circular orbits or axial tilts causes this point to move around any fixed point on the celestial body like an analemma.

gollark: Cool idea.
gollark: Ah yes, Kolmogorov complexity.
gollark: Also, human brains have weird color processing quirks because instead of answering the question "what mixture of light is entering this part of the visual field" they're solving the harder but more useful one of what color an object is and what light sources are present and that sort of thing.
gollark: The color of the thing as seen by a camera (or your eyes) depends on lighting conditions and what's near it and configuration and such.
gollark: Yes. The "RGB value" of a surface doesn't really... exist, see.

See also

References
  1. "Definition of LONGITUDE". www.merriam-webster.com. Merriam-Webster. Retrieved 14 March 2018.
  2. Oxford English Dictionary
  3. "Collecion de los viajes y descubrimientos que hicieron por mas los Españoles ..." Madrid, en la imprenta Real, 1825; pag. 272
  4. Vespucci, Amerigo. "Letter from Seville to Lorenzo di Pier Francesco de' Medici, 1500." Pohl, Frederick J. Amerigo Vespucci: Pilot Major. New York: Columbia University Press, 1945. 76–90. Page 80.
  5. "Longitude clock comes alive". BBC. March 11, 2002.
  6. Denny, Mark (2012), The Science of Navigation: From Dead Reckoning to GPS, Johns Hopkins University Press, p. 105, ISBN 9781421405605, in 1610, Galileo thought he might win the Spanish longitude prize with his idea of measuring time by observing the moons of Jupiter ... The trouble with the method was in making accurate measurements of the four moons while on the deck of a moving ship at sea. This problem proved intractable, and the method was therefore not adopted.
  7. "MONOGRAPHIE DE L'AURORE - Corvette -1766". Ancre. Retrieved 2019-12-05.
  8. "International Conference Held at Washington for the Purpose of Fixing a Prime Meridian and a Universal Day. October, 1884. Protocols of the proceedings". Project Gutenberg. 1884. Retrieved 30 November 2012.
  9. "Coordinate Conversion". colorado.edu. Archived from the original on 29 September 2009. Retrieved 14 March 2018.
  10. "λ = Longitude east of Greenwich (for longitude west of Greenwich, use a minus sign)."
    John P. Snyder, Map Projections, A Working Manual, USGS Professional Paper 1395, page ix
  11. NOAA ESRL Sunrise/Sunset Calculator (deprecated). Earth System Research Laboratory. Retrieved October 18, 2019.
  12. Read HH, Watson Janet (1975). Introduction to Geology. New York: Halsted. pp. 13–15.
  13. Osborne, Peter (2013). "Chapter 5: The geometry of the ellipsoid". The Mercator Projections: The Normal and Transverse Mercator Projections on the Sphere and the Ellipsoid with Full Derivations of all Formulae (PDF). Edinburgh. doi:10.5281/zenodo.35392. Archived from the original (PDF) on 2016-05-09. Retrieved 2016-01-24.
  14. Rapp, Richard H. (April 1991). "Chapter 3: Properties of the Ellipsoid". Geometric Geodesy Part I. Columbus, Ohio.: Department of Geodetic Science and Surveying, Ohio State University. hdl:1811/24333.
  15. Where is zero degrees longitude on Mars? – Copyright 2000 – 2010 © European Space Agency. All rights reserved.
  16. Davies, M. E., and R. A. Berg, "Preliminary Control Net of Mars,"Journal of Geophysical Research, Vol. 76, No. 2, pps. 373-393, January 10, 1971.
  17. Davies, M. E., "Surface Coordinates and Cartography of Mercury," Journal of Geophysical Research, Vol. 80, No. 17, June 10, 1975.
  18. Archinal, Brent A.; A'Hearn, Michael F.; Bowell, Edward L.; Conrad, Albert R.; et al. (2010). "Report of the IAU Working Group on Cartographic Coordinates and Rotational Elements: 2009". Celestial Mechanics and Dynamical Astronomy. 109 (2): 101–135. Bibcode:2011CeMDA.109..101A. doi:10.1007/s10569-010-9320-4. ISSN 0923-2958.
  19. "USGS Astrogeology: Rotation and pole position for the Sun and planets (IAU WGCCRE)". Archived from the original on October 24, 2011. Retrieved October 22, 2009.
  20. First map of extraterrestrial planet – Center of Astrophysics.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.