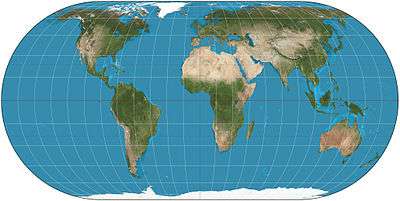
Eckert IV projection

The Eckert IV projection is an equal-area pseudocylindrical map projection. The length of the polar lines is half that of the equator, and lines of longitude are semiellipses, or portions of ellipses. It was first described by Max Eckert in 1906 as one of a series of three pairs of pseudocylindrical projections. Within each pair, meridians are the same whereas parallels differ. Odd-numbered projections have parallels spaced equally, whereas even-numbered projections have parallels spaced to preserve area. Eckert IV is paired with Eckert III.[1]

Eckert IV projection of the world.

Eckert IV projection with Tissot's indicatrices of distortion.

Formulas

Forward formulae

Given a sphere of radius R, central meridian λ₀ and a point with geographical latitude φ and longitude λ, plane coordinates x and y can be computed using the following formulas:

{\begin{aligned}x&={\frac {2}{\sqrt {4\pi +\pi ^{2}}}}R\,(\lambda -\lambda _{0})(1+\cos \theta )\approx 0.422\,2382\,R\,(\lambda -\lambda _{0})(1+\cos \theta ),\\[8pt]y&=2{\sqrt {\frac {\pi }{4+\pi }}}R\sin \theta \approx 1.326\,5004\,R\sin \theta ,\end{aligned}}

where

\theta +\sin \theta \cos \theta +2\sin \theta =\left(2+{\frac {\pi }{2}}\right)\sin \varphi .

θ can be solved for numerically using Newton's method.[2]

Inverse formulae

{\begin{aligned}\theta &=\arcsin \left[y{\frac {\sqrt {4+\pi }}{2{\sqrt {\pi }}R}}\right]\approx \arcsin \left[{\frac {y}{1.326\,5004\,R}}\right]\\[8pt]\varphi &=\arcsin \left[{\frac {\theta +\sin \theta \cos \theta +2\sin \theta }{2+{\frac {\pi }{2}}}}\right]\\[8pt]\lambda &=\lambda _{0}+x{\frac {\sqrt {4\pi +\pi ^{2}}}{2R(1+\cos \theta )}}\approx \lambda _{0}+{\frac {x}{0.422\,2382\,R\,(1+\cos \theta )}}\end{aligned}}

gollark: Mostly I just use the 3dm file saved on my workstation.

gollark: I forgot.

gollark: Who pinged me? I'm very busy.

gollark: I haven't been on in [REDACTED].

gollark: Unlikely.

References

Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 60. ISBN 978-0160033681. Retrieved 2014-09-27.
Snyder, John P. (1987). Map Projections – A Working Manual. Professional Paper 1395. Denver: USGS. pp. 253–258. ISBN 0-226-76747-7. Retrieved 2013-07-24.

External links

Eckert IV projection at Mathworld

This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.

[Snyder89-1] Snyder, John P.; Voxland, Philip M. (1989). An Album of Map Projections. Professional Paper 1453. Denver: USGS. p. 60. ISBN 978-0160033681. Retrieved 2014-09-27.

[Snyder87-2] Snyder, John P. (1987). Map Projections – A Working Manual. Professional Paper 1395. Denver: USGS. pp. 253–258. ISBN 0-226-76747-7. Retrieved 2013-07-24.