Minute and second of arc
A minute of arc, arcminute (arcmin), arc minute, or minute arc is a unit of angular measurement equal to 1/60 of one degree. Since one degree is 1/360 of a turn (or complete rotation), one minute of arc is 1/21600 of a turn. The nautical mile was originally defined as a minute of latitude on a hypothetical spherical Earth so the actual Earth circumference is very near 21 600 nautical miles. A minute of arc is π/10800 of a radian.
| Arcminute | |
|---|---|
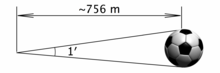 An illustration of the size of an arcminute (not to scale). A standard association football (soccer) ball (with a diameter of 22 cm or 8.7 in) subtends an angle of 1 arcminute at a distance of approximately 756 m (827 yd). | |
| General information | |
| Unit system | Non-SI units mentioned in the SI |
| Unit of | Angle |
| Symbol | ′ or arcmin |
| In units | Dimensionless with an arc length of approx. ≈ 0.2909/1000 of the radius, i.e. 0.2909 mm/m |
| Conversions | |
| 1 ′ in ... | ... is equal to ... |
| degrees | 1/60° = 0.016° |
| arcseconds | 60″ |
| radians | π/10800 ≈ 0.000290888 rad |
| milliradians | π·1000/10800 ≈ 0.2909 mrad |
| gons | 600/9g = 66.6g |
| turns | 1/21600 |
A second of arc, arcsecond (arcsec), or arc second is 1/60 of an arcminute, 1/3600 of a degree, 1/1296000 of a turn, and π/648000 (about 1/206264.8) of a radian.
These units originated in Babylonian astronomy as sexagesimal subdivisions of the degree; they are used in fields that involve very small angles, such as astronomy, optometry, ophthalmology, optics, navigation, land surveying, and marksmanship.
To express even smaller angles, standard SI prefixes can be employed; the milliarcsecond (mas) and microarcsecond (μas), for instance, are commonly used in astronomy.
The number of square arcminutes in a complete sphere is 148510660 square arcminutes (the surface area of a unit sphere in square units divided by the solid angle area subtended by a square arcminute, also in square units – so that the final result is a dimensionless number).
The fact that the terms "minute" and "second" also denote units of time derives from Babylonian astronomy, where the corresponding time-related terms denoted the duration of the Sun's apparent motion of one minute or one second of arc, respectively, through the ecliptic. In present terms, the Babylonian degree of time was four minutes long so the "minute" of time was four seconds long and the "second" 1/15 of a second.[1][2]
Symbols and abbreviations
The prime symbol (′) (U+2032) designates the arcminute, though a single quote (') (U+0027) is commonly used where only ASCII characters are permitted. One arcminute is thus written 1′. It is also abbreviated as arcmin or amin or, less commonly, the prime with a circumflex over it ().
Similarly, double prime (″) (U+2033) designates the arcsecond, though a double quote (") (U+0022) is commonly used where only ASCII characters are permitted. One arcsecond is thus written 1″. It is also abbreviated as arcsec or asec.
| Unit | Value | Symbol | Abbreviations | In radians, approx. | |
|---|---|---|---|---|---|
| Degree | 1/360 turn | ° | Degree | deg | 17.4532925 mrad |
| Arcminute | 1/60 degree | ′ | Prime | arcmin, amin, am, , MOA | 290.8882087 μrad |
| Arcsecond | 1/60 arcminute = 1/3600 degree | ″ | Double prime | arcsec, asec, as | 4.8481368 μrad |
| Milliarcsecond | 0.001 arcsecond = 1/3600000 degree | mas | 4.8481368 nrad | ||
| Microarcsecond | 0.001 mas = 0.000001 arcsecond | μas | 4.8481368 prad | ||
In celestial navigation, seconds of arc are rarely used in calculations, the preference usually being for degrees, minutes and decimals of a minute, for example, written as 42° 25.32′ or 42° 25.322′.[3][4] This notation has been carried over into marine GPS receivers, which normally display latitude and longitude in the latter format by default.[5]
Common examples
The full moon's average apparent size is about 31 arcminutes (or 0.52°).
An arcminute is approximately the resolution of the human eye.
An arcsecond is approximately the angle subtended by a U.S. dime coin (18 mm) at a distance of 4 kilometres (about 2.5 mi).[6] An arcsecond is also the angle subtended by
- an object of diameter 725.27 km at a distance of one astronomical unit,
- an object of diameter 45866916 km at one light-year,
- an object of diameter one astronomical unit (149597870.7 km) at a distance of one parsec, per the definition of the latter.[7]
A milliarcsecond is about the size of a dime atop the Eiffel Tower as seen from New York City.
A microarcsecond is about the size of a period at the end of a sentence in the Apollo mission manuals left on the Moon as seen from Earth.
A nanoarcsecond is about the size of a penny on Neptune's moon Triton as observed from Earth.
Also notable examples of size in arcseconds are:
- Hubble Space Telescope has calculational resolution of 0.05 arcseconds and actual resolution of almost 0.1 arcseconds, which is close to the diffraction limit.[8]
- crescent Venus measures between 60.2 and 66 seconds of arc.[8]
Uses
Astronomy

Since antiquity the arcminute and arcsecond have been used in astronomy. In the ecliptic coordinate system, latitude (β) and longitude (λ); in the horizon system, altitude (Alt) and azimuth (Az); and in the equatorial coordinate system, declination (δ), are all measured in degrees, arcminutes and arcseconds. The principal exception is right ascension (RA) in equatorial coordinates, which is measured in time units of hours, minutes, and seconds.
The arcsecond is also often used to describe small astronomical angles such as the angular diameters of planets (e.g. the angular diameter of Venus which varies between 10″ and 60″), the proper motion of stars, the separation of components of binary star systems, and parallax, the small change of position of a star in the course of a year or of a solar system body as the Earth rotates. These small angles may also be written in milliarcseconds (mas), or thousandths of an arcsecond. The unit of distance, the parsec, named from the parallax of one arc second, was developed for such parallax measurements. It is the distance at which the mean radius of the Earth's orbit (more precisely, one astronomical unit) would subtend an angle of one arcsecond.
The ESA astrometric satellite Gaia, launched in 2013, can approximate star positions to 7 microarcseconds (µas).[9]
Apart from the Sun, the star with the largest angular diameter from Earth is R Doradus, a red giant with a diameter of 0.05 arcsecond.[note 1] Because of the effects of atmospheric blurring, ground-based telescopes will smear the image of a star to an angular diameter of about 0.5 arcsecond; in poor conditions this increases to 1.5 arcseconds or even more. The dwarf planet Pluto has proven difficult to resolve because its angular diameter is about 0.1 arcsecond.[11]
Space telescopes are not affected by the Earth's atmosphere but are diffraction limited. For example, the Hubble Space Telescope can reach an angular size of stars down to about 0.1″. Techniques exist for improving seeing on the ground. Adaptive optics, for example, can produce images around 0.05 arcsecond on a 10 m class telescope.
Cartography
Minutes (′) and seconds (″) of arc are also used in cartography and navigation. At sea level one minute of arc along the equator or a meridian (indeed, any great circle) equals exactly one geographical mile along the Earth's equator or approximately one nautical mile (1,852 metres; 1.151 miles).[12] A second of arc, one sixtieth of this amount, is roughly 30 metres (98 feet). The exact distance varies along meridian arcs because the figure of the Earth is slightly oblate (bulges a third of a percent at the equator).
Positions are traditionally given using degrees, minutes, and seconds of arcs for latitude, the arc north or south of the equator, and for longitude, the arc east or west of the Prime Meridian. Any position on or above the Earth's reference ellipsoid can be precisely given with this method. However, when it is inconvenient to use base-60 for minutes and seconds, positions are frequently expressed as decimal fractional degrees to an equal amount of precision. Degrees given to three decimal places (1/1000 of a degree) have about 1/4 the precision of degrees-minutes-seconds (1/3600 of a degree) and specify locations within about 120 metres (390 feet). For navigational purposes positions are given in degrees and decimal minutes, for instance The Needles lighthouse is at 50º 39.734’N 001º 35.500’W.[13]
Property cadastral surveying
Related to cartography, property boundary surveying using the metes and bounds system relies on fractions of a degree to describe property lines' angles in reference to cardinal directions. A boundary "mete" is described with a beginning reference point, the cardinal direction North or South followed by an angle less than 90 degrees and a second cardinal direction, and a linear distance. The boundary runs the specified linear distance from the beginning point, the direction of the distance being determined by rotating the first cardinal direction the specified angle toward the second cardinal direction. For example, North 65° 39′ 18″ West 85.69 feet would describe a line running from the starting point 85.69 feet in a direction 65° 39′ 18″ (or 65.655°) away from north toward the west.
Firearms
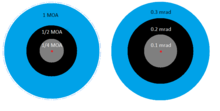
.png)
The arcminute is commonly found in the firearms industry and literature, particularly concerning the precision of rifles, though the industry refers to it as minute of angle (MOA). It is especially popular as a unit of measurement with shooters familiar with the imperial measurement system because 1 MOA subtends a circle with a diameter of 1.047 inches (which is often rounded to just 1 inch) at 100 yards (2.908 cm at 100 m), a traditional distance on American target ranges. The subtension is linear with the distance, for example, at 500 yards, 1 MOA subtends 5.235 inches, and at 1000 yards 1 MOA subtends 10.47 inches. Since many modern telescopic sights are adjustable in half (1/2), quarter (1/4) or eighth (1/8) MOA increments, also known as clicks, zeroing and adjustments are made by counting 2, 4 and 8 clicks per MOA respectively.
For example, if the point of impact is 3 inches high and 1.5 inches left of the point of aim at 100 yards (which for instance could be measured by using a spotting scope with a calibrated reticle), the scope needs to be adjusted 3 MOA down, and 1.5 MOA right. Such adjustments are trivial when the scope's adjustment dials have a MOA scale printed on them, and even figuring the right number of clicks is relatively easy on scopes that click in fractions of MOA. This makes zeroing and adjustments much easier:
- To adjust a 1⁄2 MOA scope 3 MOA down and 1.5 MOA right, the scope needs to be adjusted 3 × 2 = 6 clicks down and 1.5 x 2 = 3 clicks right
- To adjust a 1⁄4 MOA scope 3 MOA down and 1.5 MOA right, the scope needs to be adjusted 3 x 4 = 12 clicks down and 1.5 × 4 = 6 clicks right
- To adjust a 1⁄8 MOA scope 3 MOA down and 1.5 MOA right, the scope needs to be adjusted 3 x 8 = 24 clicks down and 1.5 × 8 = 12 clicks right
Another common system of measurement in firearm scopes is the milliradian (mrad). Zeroing an mrad based scope is easy for users familiar with base ten systems. The most common adjustment value in mrad based scopes is 1/10 mrad (which approximates 1⁄3 MOA).
- To adjust a 1/10 mrad scope 0.9 mrad down and 0.4 mrad right, the scope needs to be adjusted 9 clicks down and 4 clicks right (which equals approximately 3 and 1.5 MOA respectively).
One thing to be aware of is that some MOA scopes, including some higher-end models, are calibrated such that an adjustment of 1 MOA on the scope knobs corresponds to exactly 1 inch of impact adjustment on a target at 100 yards, rather than the mathematically correct 1.047". This is commonly known as the Shooter's MOA (SMOA) or Inches Per Hundred Yards (IPHY). While the difference between one true MOA and one SMOA is less than half of an inch even at 1000 yards,[14] this error compounds significantly on longer range shots that may require adjustment upwards of 20–30 MOA to compensate for the bullet drop. If a shot requires an adjustment of 20 MOA or more, the difference between true MOA and SMOA will add up to 1 inch or more. In competitive target shooting, this might mean the difference between a hit and a miss.
The physical group size equivalent to m minutes of arc can be calculated as follows: group size = tan(m/60) × distance. In the example previously given, for 1 minute of arc, and substituting 3,600 inches for 100 yards, 3,600 tan(1/60) ≈ 1.047 inches. In metric units 1 MOA at 100 metres ≈ 2.908 centimetres.
Sometimes, a precision-oriented firearm's performance will be measured in MOA. This simply means that under ideal conditions (i.e. no wind, high-grade ammo, clean barrel, and a stable mounting platform such as a vise or a benchrest used to eliminate shooter error), the gun is capable of producing a group of shots whose center points (center-to-center) fit into a circle, the average diameter of circles in several groups can be subtended by that amount of arc. For example, a 1 MOA rifle should be capable, under ideal conditions, of repeatably shooting 1-inch groups at 100 yards. Most higher-end rifles are warrantied by their manufacturer to shoot under a given MOA threshold (typically 1 MOA or better) with specific ammunition and no error on the shooter's part. For example, Remington's M24 Sniper Weapon System is required to shoot 0.8 MOA or better, or be rejected from sale by quality control.
Rifle manufacturers and gun magazines often refer to this capability as sub-MOA, meaning a gun consistently shooting groups under 1 MOA. This means that a single group of 3 to 5 shots at 100 yards, or the average of several groups, will measure less than 1 MOA between the two furthest shots in the group, i.e. all shots fall within 1 MOA. If larger samples are taken (i.e., more shots per group) then group size typically increases, however this will ultimately average out. If a rifle was truly a 1 MOA rifle, it would be just as likely that two consecutive shots land exactly on top of each other as that they land 1 MOA apart. For 5-shot groups, based on 95% confidence, a rifle that normally shoots 1 MOA can be expected to shoot groups between 0.58 MOA and 1.47 MOA, although the majority of these groups will be under 1 MOA. What this means in practice is if a rifle that shoots 1-inch groups on average at 100 yards shoots a group measuring 0.7 inches followed by a group that is 1.3 inches, this is not statistically abnormal.[15][16]
The Metric System counterpart of the MOA is the milliradian or mrad, being equal to one 1000th of the target range, laid out on a circle that has the observer as centre and the target range as radius. The number of milliradians on a full such circle therefore always is equal to 2 × π × 1000, regardless the target range. Therefore, 1 MOA ≈ 0.2909 mrad. This means that an object which spans 1 mrad on the reticle is at a range that is in metres equal to the object's size in millimetres (e.g. an object of 100 mm @ 1 mrad is 100 metres away). So there is no conversion factor required, contrary to the MOA system. A reticle with markings (hashes or dots) spaced with a one mrad apart (or a fraction of a mrad) are collectively called a mrad reticle. If the markings are round they are called mil-dots.
In the table below conversions from mrad to metric values are exact (e.g. 0.1 mrad equals exactly 10 mm at 100 metres), while conversions of minutes of arc to both metric and imperial values are approximate.
| Angle adjustment per click |
Minutes of arc |
Milli- radians |
At 100 m | At 100 yd | ||
|---|---|---|---|---|---|---|
| mm | cm | in | in | |||
| 1⁄12′ | 0.083′ | 0.024 mrad | 2.42 mm | 0.242 cm | 0.0958 in | 0.087 in |
| 0.25⁄10 mrad | 0.086′ | 0.025 mrad | 2.5 mm | 0.25 cm | 0.0985 in | 0.09 in |
| 1⁄8′ | 0.125′ | 0.036 mrad | 3.64 mm | 0.36 cm | 0.144 in | 0.131 in |
| 1⁄6′ | 0.167′ | 0.0485 mrad | 4.85 mm | 0.485 cm | 0.192 in | 0.175 in |
| 0.5⁄10 mrad | 0.172′ | 0.05 mrad | 5 mm | 0.5 cm | 0.197 in | 0.18 in |
| 1⁄4′ | 0.25′ | 0.073 mrad | 7.27 mm | 0.73 cm | 0.29 in | 0.26 in |
| 1⁄10 mrad | 0.344′ | 0.1 mrad | 10 mm | 1 cm | 0.39 in | 0.36 in |
| 1⁄2′ | 0.5′ | 0.145 mrad | 14.54 mm | 1.45 cm | 0.57 in | 0.52 in |
| 1.5⁄10 mrad | 0.516′ | 0.15 mrad | 15 mm | 1.5 cm | 0.59 in | 0.54 in |
| 2⁄10 mrad | 0.688′ | 0.2 mrad | 20 mm | 2 cm | 0.79 in | 0.72 in |
| 1′ | 1.0′ | 0.291 mrad | 29.1 mm | 2.91 cm | 1.15 in | 1.047 in |
| 1 mrad | 3.438′ | 1 mrad | 100 mm | 10 cm | 3.9 in | 3.6 in |
- 1′ at 100 yards is about 1.047 inches[17]
- 1′ ≈ 0.291 mrad (or 29.1 mm at 100 m, approximately 30 mm at 100 m)
- 1 mrad ≈ 3.44′, so 1/10 mrad ≈ 1/3′
- 0.1 mrad equals exactly 1 cm at 100 m, or approximately 0.36 inches at 100 yards
Human vision
In humans, 20/20 vision is the ability to resolve a spatial pattern separated by a visual angle of one minute of arc. A 20/20 letter subtends 5 minutes of arc total.
Materials
The deviation from parallelism between two surfaces, for instance in optical engineering, is usually measured in arcminutes or arcseconds. In addition, arcseconds are sometimes used in rocking curve (ω-scan) x ray diffraction measurements of high-quality epitaxial thin films.
Manufacturing
Some measurement devices make use of arcminutes and arcseconds to measure angles when the object being measured is too small for direct visual inspection. For instance, a toolmaker's optical comparator will often include an option to measure in "minutes and seconds".
See also
- Degree (angle) § Subdivisions
- Sexagesimal § Modern usage
- Square minute
- Square second
- Milliradian
Notes
- Some studies have shown a larger angular diameter for Betelgeuse. Various studies have produced figures of between 0.042 and 0.069 arcseconds for the star's diameter. The variability of Betelgeuse and difficulties in producing a precise reading for its angular diameter make any definitive figure conjectural.
References
- Correll, Malcolm (November 1977). "Early Time Measurements". The Physics Teacher. 15 (8): 476–479. doi:10.1119/1.2339739.
- F. Richard Stephenson; Louay J. Fatoohi (May 1994). "The Babylonian Unit of Time". Journal for the History of Astronomy. doi:10.1177/002182869402500203.
- "CELESTIAL NAVIGATION COURSE". International Navigation School. Retrieved 4 November 2010.
It is a straightforward method [to obtain a position at sea] and requires no mathematical calculation beyond addition and subtraction of degrees and minutes and decimals of minutes
- "Astro Navigation Syllabus". Retrieved 4 November 2010.
[Sextant errors] are sometimes [given] in seconds of arc, which will need to be converted to decimal minutes when you include them in your calculation.
- "Shipmate GN30". Norinco. Archived from the original on 24 January 2008. Retrieved 4 November 2010.
- Filippenko, Alex, Understanding the Universe (of The Great Courses, on DVD), Lecture 43, time 12:05, The Teaching Company, Chantilly, VA, USA, 2007.
- "Cosmic Distance Scales - The Milky Way".
- "The Diffraction Limit of a Telescope".
- Amos, Jonathan (14 September 2016). "Celestial mapper plots a billion stars". BBC News. Retrieved 31 March 2018.
- "ESO Telescope Images Stunning Central Region of Milky Way, Finds Ancient Star Burst". www.eso.org. Retrieved 18 December 2019.
- NASA.gov Pluto Fact Sheet
- Kaplan, George H. (1 January 2003). "Nautical mile approximates an arcminute". Ocean Navigator. Navigator Publishing. Retrieved 22 March 2017.
- The Corporation of Trinity House (10 January 2020). "1/2020 Needles Lighthouse". Notices to Mariners. Retrieved 24 May 2020.
- Mann, Richard (18 February 2011). "Mil, MOA or inches?". Shooting Illustrated. Archived from the original on 10 November 2013. Retrieved 13 April 2015.
- Wheeler, Robert E. "Statistical notes on rifle group patterns" (PDF). Archived from the original (PDF) on 26 September 2006. Retrieved 21 May 2009.
- Bramwell, Denton (January 2009). "Group Therapy The Problem: How accurate is your rifle?". Varmint Hunter. 69. Archived from the original on 7 October 2011. Retrieved 21 May 2009.
- Dexadine Ballistics Software – ballistic data for shooting and reloading. See Talk
External links
- MOA / mils By Robert Simeone
- A Guide to calculate distance using MOA Scope by Steve Coffman

