0
0 (zero) is a number,[1] and the numerical digit used to represent that number in numerals. It fulfills a central role in mathematics as the additive identity[2] of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems. Names for the number 0 in English include zero, nought (UK), naught (US) (/nɔːt/), nil, or—in contexts where at least one adjacent digit distinguishes it from the letter "O"—oh or o (/oʊ/). Informal or slang terms for zero include zilch and zip.[3] Ought and aught (/ɔːt/),[4] as well as cipher,[5] have also been used historically.[6][7]
| ||||
|---|---|---|---|---|
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] | ||||
| Cardinal | 0, zero, "oh" (/oʊ/), nought, naught, nil | |||
| Ordinal | Zeroth, noughth | |||
| Divisors | All numbers | |||
| Binary | 02 | |||
| Ternary | 03 | |||
| Quaternary | 04 | |||
| Quinary | 05 | |||
| Senary | 06 | |||
| Octal | 08 | |||
| Duodecimal | 012 | |||
| Hexadecimal | 016 | |||
| Vigesimal | 020 | |||
| Base 36 | 036 | |||
| Arabic, Kurdish, Persian, Sindhi, Urdu | ٠ | |||
| Bengali | ০ | |||
| Hindu Numerals | ० | |||
| Chinese | 零, 〇 | |||
| Khmer | ០ | |||
| Thai | ๐ | |||
Etymology
The word zero came into the English language via French zéro from Italian zero, Italian contraction of Venetian zevero form of Italian zefiro via ṣafira or ṣifr.[8] In pre-Islamic time the word ṣifr (Arabic صفر) had the meaning "empty".[9] Sifr evolved to mean zero when it was used to translate śūnya (Sanskrit: शून्य) from India.[9] The first known English use of zero was in 1598.[10]
The Italian mathematician Fibonacci (c. 1170–1250), who grew up in North Africa and is credited with introducing the decimal system to Europe, used the term zephyrum. This became zefiro in Italian, and was then contracted to zero in Venetian. The Italian word zefiro was already in existence (meaning "west wind" from Latin and Greek zephyrus) and may have influenced the spelling when transcribing Arabic ṣifr.[11]
Modern usage
Depending on the context, there may be different words used for the number zero (or the concept of zero). For the simple notion of lacking, the words nothing and none are often used. Sometimes, the words nought, naught and aught[12] are used. Several sports have specific words for a score of zero, such as love in tennis and duck in cricket; nil is used for many sports in British English. It is often called oh in the context of telephone numbers. Slang words for zero include zip, zilch, nada, and scratch. Duck egg and goose egg are also slang for zero.[13]
History
Ancient Near East
| nfr |
heart with trachea beautiful, pleasant, good |
|---|
Ancient Egyptian numerals were of base 10.[14] They used hieroglyphs for the digits and were not positional. By 1770 BC, the Egyptians had a symbol for zero in accounting texts. The symbol nfr, meaning beautiful, was also used to indicate the base level in drawings of tombs and pyramids, and distances were measured relative to the base line as being above or below this line.[15]
By the middle of the 2nd millennium BC, the Babylonian mathematics had a sophisticated sexagesimal positional numeral system. The lack of a positional value (or zero) was indicated by a space between sexagesimal numerals. By 300 BC, a punctuation symbol (two slanted wedges) was co-opted as a placeholder in the same Babylonian system. In a tablet unearthed at Kish (dating from about 700 BC), the scribe Bêl-bân-aplu wrote his zeros with three hooks, rather than two slanted wedges.[16]
The Babylonian placeholder was not a true zero because it was not used alone, nor was it used at the end of a number. Thus numbers like 2 and 120 (2×60), 3 and 180 (3×60), 4 and 240 (4×60) looked the same, because the larger numbers lacked a final sexagesimal placeholder. Only context could differentiate them.
Pre-Columbian Americas
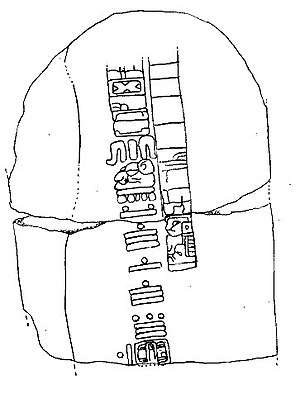
The Mesoamerican Long Count calendar developed in south-central Mexico and Central America required the use of zero as a placeholder within its vigesimal (base-20) positional numeral system. Many different glyphs, including this partial quatrefoil—![]()
Since the eight earliest Long Count dates appear outside the Maya homeland,[17] it is generally believed that the use of zero in the Americas predated the Maya and was possibly the invention of the Olmecs.[18] Many of the earliest Long Count dates were found within the Olmec heartland, although the Olmec civilization ended by the 4th century BC, several centuries before the earliest known Long Count dates.
Although zero became an integral part of Maya numerals, with a different, empty tortoise-like "shell shape" used for many depictions of the "zero" numeral, it is assumed to have not influenced Old World numeral systems.
Quipu, a knotted cord device, used in the Inca Empire and its predecessor societies in the Andean region to record accounting and other digital data, is encoded in a base ten positional system. Zero is represented by the absence of a knot in the appropriate position.
Classical antiquity
The ancient Greeks had no symbol for zero (μηδέν), and did not use a digit placeholder for it.[19] They seemed unsure about the status of zero as a number. They asked themselves, "How can nothing be something?", leading to philosophical and, by the medieval period, religious arguments about the nature and existence of zero and the vacuum. The paradoxes of Zeno of Elea depend in large part on the uncertain interpretation of zero.[20]

By AD 150, Ptolemy, influenced by Hipparchus and the Babylonians, was using a symbol for zero ()[21][22] in his work on mathematical astronomy called the Syntaxis Mathematica, also known as the Almagest.[23] This Hellenistic zero was perhaps the earliest documented use of a numeral representing zero in the Old World.[24] Ptolemy used it many times in his Almagest (VI.8) for the magnitude of solar and lunar eclipses. It represented the value of both digits and minutes of immersion at first and last contact. Digits varied continuously from 0 to 12 to 0 as the Moon passed over the Sun (a triangular pulse), where twelve digits was the angular diameter of the Sun. Minutes of immersion was tabulated from 0′0″ to 31′20″ to 0′0″, where 0′0″ used the symbol as a placeholder in two positions of his sexagesimal positional numeral system,[lower-alpha 2] while the combination meant a zero angle. Minutes of immersion was also a continuous function 1/12 31′20″ √d(24−d) (a triangular pulse with convex sides), where d was the digit function and 31′20″ was the sum of the radii of the Sun's and Moon's discs.[25] Ptolemy's symbol was a placeholder as well as a number used by two continuous mathematical functions, one within another, so it meant zero, not none.
The earliest use of zero in the calculation of the Julian Easter occurred before AD 311, at the first entry in a table of epacts as preserved in an Ethiopic document for the years AD 311 to 369, using a Ge'ez word for "none" (English translation is "0" elsewhere) alongside Ge'ez numerals (based on Greek numerals), which was translated from an equivalent table published by the Church of Alexandria in Medieval Greek.[26] This use was repeated in AD 525 in an equivalent table, that was translated via the Latin nulla or "none" by Dionysius Exiguus, alongside Roman numerals.[27] When division produced zero as a remainder, nihil, meaning "nothing", was used. These medieval zeros were used by all future medieval calculators of Easter. The initial "N" was used as a zero symbol in a table of Roman numerals by Bede—or his colleagues around AD 725.[28]
China
The Sūnzĭ Suànjīng, of unknown date but estimated to be dated from the 1st to 5th centuries AD, and Japanese records dated from the 18th century, describe how the c. 4th century BC Chinese counting rods system enabled one to perform decimal calculations. As noted in Xiahou Yang’s Suanjing (425–468 AD) that states that to multiply or divide a number by 10, 100, 1000, or 10000, all one needs to do, with rods on the counting board, is to move them forwards, or back, by 1, 2, 3, or 4 places,[30] According to A History of Mathematics, the rods "gave the decimal representation of a number, with an empty space denoting zero."[29] The counting rod system is considered a positional notation system.[31]
In AD 690, Empress Wǔ promulgated Zetian characters, one of which was "〇". The symbol 0 for denoting zero is a variation of this character.
Zero was not treated as a number at that time, but as a "vacant position".[32] Qín Jiǔsháo's 1247 Mathematical Treatise in Nine Sections is the oldest surviving Chinese mathematical text using a round symbol for zero.[33] Chinese authors had been familiar with the idea of negative numbers by the Han Dynasty (2nd century AD), as seen in The Nine Chapters on the Mathematical Art.[34]
India
Pingala (c. 3rd/2nd century BC[35]), a Sanskrit prosody scholar,[36] used binary numbers in the form of short and long syllables (the latter equal in length to two short syllables), a notation similar to Morse code.[37] Pingala used the Sanskrit word śūnya explicitly to refer to zero.[38]
The concept of zero as a written digit in the decimal place value notation was developed in India, presumably as early as during the Gupta period (c. 5th century), with the oldest unambiguous evidence dating to the 7th century.[39]
A symbol for zero, a large dot likely to be the precursor of the still-current hollow symbol, is used throughout the Bakhshali manuscript, a practical manual on arithmetic for merchants.[40] In 2017, three samples from the manuscript were shown by radiocarbon dating to come from three different centuries: from AD 224–383, AD 680–779, and AD 885–993, making it South Asia’s oldest recorded use of the zero symbol. It is not known how the birch bark fragments from different centuries forming the manuscript came to be packaged together.[41][42][43]
The Lokavibhāga, a Jain text on cosmology surviving in a medieval Sanskrit translation of the Prakrit original, which is internally dated to AD 458 (Saka era 380), uses a decimal place-value system, including a zero. In this text, śūnya ("void, empty") is also used to refer to zero.[44]
The Aryabhatiya (c. 500), states sthānāt sthānaṁ daśaguṇaṁ syāt "from place to place each is ten times the preceding."[45][45][46][47]
Rules governing the use of zero appeared in Brahmagupta's Brahmasputha Siddhanta (7th century), which states the sum of zero with itself as zero, and incorrectly division by zero as:[48][49]
A positive or negative number when divided by zero is a fraction with the zero as denominator. Zero divided by a negative or positive number is either zero or is expressed as a fraction with zero as numerator and the finite quantity as denominator. Zero divided by zero is zero.
Epigraphy

There are numerous copper plate inscriptions, with the same small o in them, some of them possibly dated to the 6th century, but their date or authenticity may be open to doubt.[16]
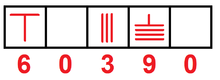
A stone tablet found in the ruins of a temple near Sambor on the Mekong, Kratié Province, Cambodia, includes the inscription of "605" in Khmer numerals (a set of numeral glyphs for the Hindu–Arabic numeral system). The number is the year of the inscription in the Saka era, corresponding to a date of AD 683.[50]
The first known use of special glyphs for the decimal digits that includes the indubitable appearance of a symbol for the digit zero, a small circle, appears on a stone inscription found at the Chaturbhuj Temple, Gwalior, in India, dated 876.[51][52] Zero is also used as a placeholder in the Bakhshali manuscript, portions of which date from AD 224–383.[53]
Middle Ages
Transmission to Islamic culture
The Arabic-language inheritance of science was largely Greek,[54] followed by Hindu influences.[55] In 773, at Al-Mansur's behest, translations were made of many ancient treatises including Greek, Roman, Indian, and others.
In AD 813, astronomical tables were prepared by a Persian mathematician, Muḥammad ibn Mūsā al-Khwārizmī, using Hindu numerals;[55] and about 825, he published a book synthesizing Greek and Hindu knowledge and also contained his own contribution to mathematics including an explanation of the use of zero.[56] This book was later translated into Latin in the 12th century under the title Algoritmi de numero Indorum. This title means "al-Khwarizmi on the Numerals of the Indians". The word "Algoritmi" was the translator's Latinization of Al-Khwarizmi's name, and the word "Algorithm" or "Algorism" started to acquire a meaning of any arithmetic based on decimals.[55]
Muhammad ibn Ahmad al-Khwarizmi, in 976, stated that if no number appears in the place of tens in a calculation, a little circle should be used "to keep the rows". This circle was called ṣifr.[57]
Transmission to Europe
The Hindu–Arabic numeral system (base 10) reached Europe in the 11th century, via Al-Andalus through Spanish Muslims, the Moors, together with knowledge of astronomy and instruments like the astrolabe, first imported by Gerbert of Aurillac. For this reason, the numerals came to be known in Europe as "Arabic numerals". The Italian mathematician Fibonacci or Leonardo of Pisa was instrumental in bringing the system into European mathematics in 1202, stating:
After my father's appointment by his homeland as state official in the customs house of Bugia for the Pisan merchants who thronged to it, he took charge; and in view of its future usefulness and convenience, had me in my boyhood come to him and there wanted me to devote myself to and be instructed in the study of calculation for some days. There, following my introduction, as a consequence of marvelous instruction in the art, to the nine digits of the Hindus, the knowledge of the art very much appealed to me before all others, and for it I realized that all its aspects were studied in Egypt, Syria, Greece, Sicily, and Provence, with their varying methods; and at these places thereafter, while on business. I pursued my study in depth and learned the give-and-take of disputation. But all this even, and the algorism, as well as the art of Pythagoras, I considered as almost a mistake in respect to the method of the Hindus (Modus Indorum). Therefore, embracing more stringently that method of the Hindus, and taking stricter pains in its study, while adding certain things from my own understanding and inserting also certain things from the niceties of Euclid's geometric art. I have striven to compose this book in its entirety as understandably as I could, dividing it into fifteen chapters. Almost everything which I have introduced I have displayed with exact proof, in order that those further seeking this knowledge, with its pre-eminent method, might be instructed, and further, in order that the Latin people might not be discovered to be without it, as they have been up to now. If I have perchance omitted anything more or less proper or necessary, I beg indulgence, since there is no one who is blameless and utterly provident in all things. The nine Indian figures are: 9 8 7 6 5 4 3 2 1. With these nine figures, and with the sign 0 ... any number may be written.[58][59][60]
Here Leonardo of Pisa uses the phrase "sign 0", indicating it is like a sign to do operations like addition or multiplication. From the 13th century, manuals on calculation (adding, multiplying, extracting roots, etc.) became common in Europe where they were called algorismus after the Persian mathematician al-Khwārizmī. The most popular was written by Johannes de Sacrobosco, about 1235 and was one of the earliest scientific books to be printed in 1488. Until the late 15th century, Hindu–Arabic numerals seem to have predominated among mathematicians, while merchants preferred to use the Roman numerals. In the 16th century, they became commonly used in Europe.
Mathematics
0 is the integer immediately preceding 1. Zero is an even number[61] because it is divisible by 2 with no remainder. 0 is neither positive nor negative.[62] Many definitions[63] include 0 as a natural number, in which case it is the only natural number that is not positive. Zero is a number which quantifies a count or an amount of null size. In most cultures, 0 was identified before the idea of negative things (i.e., quantities less than zero) was accepted.
As a value or a number, zero is not the same as the digit zero, used in numeral systems with positional notation. Successive positions of digits have higher weights, so the digit zero is used inside a numeral to skip a position and give appropriate weights to the preceding and following digits. A zero digit is not always necessary in a positional number system (e.g., the number 02). In some instances, a leading zero may be used to distinguish a number.
Elementary algebra
The number 0 is the smallest non-negative integer. The natural number following 0 is 1 and no natural number precedes 0. The number 0 may or may not be considered a natural number, but it is an integer, and hence a rational number and a real number (as well as an algebraic number and a complex number).
The number 0 is neither positive nor negative, and is usually displayed as the central number in a number line. It is neither a prime number nor a composite number. It cannot be prime because it has an infinite number of factors, and cannot be composite because it cannot be expressed as a product of prime numbers (as 0 must always be one of the factors).[64] Zero is, however, even (i.e. a multiple of 2, as well as being a multiple of any other integer, rational, or real number).
The following are some basic (elementary) rules for dealing with the number 0. These rules apply for any real or complex number x, unless otherwise stated.
- Addition: x + 0 = 0 + x = x. That is, 0 is an identity element (or neutral element) with respect to addition.
- Subtraction: x − 0 = x and 0 − x = −x.
- Multiplication: x · 0 = 0 · x = 0.
- Division: 0/x = 0, for nonzero x. But x/0 is undefined, because 0 has no multiplicative inverse (no real number multiplied by 0 produces 1), a consequence of the previous rule.
- Exponentiation: x0 = x/x = 1, except that the case x = 0 may be left undefined in some contexts. For all positive real x, 0x = 0.
The expression 0/0, which may be obtained in an attempt to determine the limit of an expression of the form f(x)/g(x) as a result of applying the lim operator independently to both operands of the fraction, is a so-called "indeterminate form". That does not simply mean that the limit sought is necessarily undefined; rather, it means that the limit of f(x)/g(x), if it exists, must be found by another method, such as l'Hôpital's rule.
The sum of 0 numbers (the empty sum) is 0, and the product of 0 numbers (the empty product) is 1. The factorial 0! evaluates to 1, as a special case of the empty product.
Other branches of mathematics
- In set theory, 0 is the cardinality of the empty set: if one does not have any apples, then one has 0 apples. In fact, in certain axiomatic developments of mathematics from set theory, 0 is defined to be the empty set. When this is done, the empty set is the von Neumann cardinal assignment for a set with no elements, which is the empty set. The cardinality function, applied to the empty set, returns the empty set as a value, thereby assigning it 0 elements.
- Also in set theory, 0 is the lowest ordinal number, corresponding to the empty set viewed as a well-ordered set.
- In propositional logic, 0 may be used to denote the truth value false.
- In abstract algebra, 0 is commonly used to denote a zero element, which is a neutral element for addition (if defined on the structure under consideration) and an absorbing element for multiplication (if defined).
- In lattice theory, 0 may denote the bottom element of a bounded lattice.
- In category theory, 0 is sometimes used to denote an initial object of a category.
- In recursion theory, 0 can be used to denote the Turing degree of the partial computable functions.
Related mathematical terms
- A zero of a function f is a point x in the domain of the function such that f(x) = 0. When there are finitely many zeros these are called the roots of the function. This is related to zeros of a holomorphic function.
- The zero function (or zero map) on a domain D is the constant function with 0 as its only possible output value, i.e., the function f defined by f(x) = 0 for all x in D. The zero function is the only function that is both even and odd. A particular zero function is a zero morphism in category theory; e.g., a zero map is the identity in the additive group of functions. The determinant on non-invertible square matrices is a zero map.
- Several branches of mathematics have zero elements, which generalize either the property 0 + x = x, or the property 0 · x = 0, or both.
Physics
The value zero plays a special role for many physical quantities. For some quantities, the zero level is naturally distinguished from all other levels, whereas for others it is more or less arbitrarily chosen. For example, for an absolute temperature (as measured in kelvins), zero is the lowest possible value (negative temperatures are defined, but negative-temperature systems are not actually colder). This is in contrast to for example temperatures on the Celsius scale, where zero is arbitrarily defined to be at the freezing point of water. Measuring sound intensity in decibels or phons, the zero level is arbitrarily set at a reference value—for example, at a value for the threshold of hearing. In physics, the zero-point energy is the lowest possible energy that a quantum mechanical physical system may possess and is the energy of the ground state of the system.
Chemistry
Zero has been proposed as the atomic number of the theoretical element tetraneutron. It has been shown that a cluster of four neutrons may be stable enough to be considered an atom in its own right. This would create an element with no protons and no charge on its nucleus.
As early as 1926, Andreas von Antropoff coined the term neutronium for a conjectured form of matter made up of neutrons with no protons, which he placed as the chemical element of atomic number zero at the head of his new version of the periodic table. It was subsequently placed as a noble gas in the middle of several spiral representations of the periodic system for classifying the chemical elements.
Computer science
The most common practice throughout human history has been to start counting at one, and this is the practice in early classic computer programming languages such as Fortran and COBOL. However, in the late 1950s LISP introduced zero-based numbering for arrays while Algol 58 introduced completely flexible basing for array subscripts (allowing any positive, negative, or zero integer as base for array subscripts), and most subsequent programming languages adopted one or other of these positions. For example, the elements of an array are numbered starting from 0 in C, so that for an array of n items the sequence of array indices runs from 0 to n−1. This permits an array element's location to be calculated by adding the index directly to address of the array, whereas 1-based languages precalculate the array's base address to be the position one element before the first.
There can be confusion between 0- and 1-based indexing, for example Java's JDBC indexes parameters from 1 although Java itself uses 0-based indexing.
In databases, it is possible for a field not to have a value. It is then said to have a null value.[65] For numeric fields it is not the value zero. For text fields this is not blank nor the empty string. The presence of null values leads to three-valued logic. No longer is a condition either true or false, but it can be undetermined. Any computation including a null value delivers a null result.
A null pointer is a pointer in a computer program that does not point to any object or function. In C, the integer constant 0 is converted into the null pointer at compile time when it appears in a pointer context, and so 0 is a standard way to refer to the null pointer in code. However, the internal representation of the null pointer may be any bit pattern (possibly different values for different data types).
In mathematics −0 = +0 = 0; both −0 and +0 represent exactly the same number, i.e., there is no "positive zero" or "negative zero" distinct from zero. However, in some computer hardware signed number representations, zero has two distinct representations, a positive one grouped with the positive numbers and a negative one grouped with the negatives; this kind of dual representation is known as signed zero, with the latter form sometimes called negative zero. These representations include the signed magnitude and one's complement binary integer representations (but not the two's complement binary form used in most modern computers), and most floating point number representations (such as IEEE 754 and IBM S/390 floating point formats).
In binary, 0 represents the value for "off", which means no electricity flow.[66]
Zero is the value of false in many programming languages.
The Unix epoch (the date and time associated with a zero timestamp) begins the midnight before the first of January 1970.[67][68][69]
The MacOS epoch and Palm OS epoch (the date and time associated with a zero timestamp) begins the midnight before the first of January 1904.[70]
Many APIs and operating systems that require applications to return an integer value as an exit status typically use zero to indicate success and non-zero values to indicate specific error or warning conditions.
Other fields
- In telephony, pressing 0 is often used for dialling out of a company network or to a different city or region, and 00 is used for dialling abroad. In some countries, dialling 0 places a call for operator assistance.
- DVDs that can be played in any region are sometimes referred to as being "region 0"
- Roulette wheels usually feature a "0" space (and sometimes also a "00" space), whose presence is ignored when calculating payoffs (thereby allowing the house to win in the long run).
- In Formula One, if the reigning World Champion no longer competes in Formula One in the year following their victory in the title race, 0 is given to one of the drivers of the team that the reigning champion won the title with. This happened in 1993 and 1994, with Damon Hill driving car 0, due to the reigning World Champion (Nigel Mansell and Alain Prost respectively) not competing in the championship.
- On the U.S. Interstate Highway System, in most states exits are numbered based on the nearest milepost from the highway's western or southern terminus within that state. Several that are less than half a mile (800 m) from state boundaries in that direction are numbered as Exit 0.
Symbols and representations
The modern numerical digit 0 is usually written as a circle or ellipse. Traditionally, many print typefaces made the capital letter O more rounded than the narrower, elliptical digit 0.[71] Typewriters originally made no distinction in shape between O and 0; some models did not even have a separate key for the digit 0. The distinction came into prominence on modern character displays.[71]
A slashed zero can be used to distinguish the number from the letter. The digit 0 with a dot in the center seems to have originated as an option on IBM 3270 displays and has continued with some modern computer typefaces such as Andalé Mono, and in some airline reservation systems. One variation uses a short vertical bar instead of the dot. Some fonts designed for use with computers made one of the capital-O–digit-0 pair more rounded and the other more angular (closer to a rectangle). A further distinction is made in falsification-hindering typeface as used on German car number plates by slitting open the digit 0 on the upper right side. Sometimes the digit 0 is used either exclusively, or not at all, to avoid confusion altogether.
Year label
In the BC calendar era, the year 1 BC is the first year before AD 1; there is not a year zero. By contrast, in astronomical year numbering, the year 1 BC is numbered 0, the year 2 BC is numbered −1, and so forth.[72]
See also
Notes
- No long count date actually using the number 0 has been found before the 3rd century AD, but since the long count system would make no sense without some placeholder, and since Mesoamerican glyphs do not typically leave empty spaces, these earlier dates are taken as indirect evidence that the concept of 0 already existed at the time.
- Each place in Ptolemy's sexagesimal system was written in Greek numerals from 0 to 59, where 31 was written λα meaning 30+1, and 20 was written κ meaning 20.
References
- Matson, John (21 August 2009). "The Origin of Zero". Scientific American. Springer Nature. Retrieved 24 April 2016.
- "Compendium of Mathematical Symbols: Key Mathematical Numbers". Math Vault. 2020-03-01. Retrieved 2020-08-09.
- Soanes, Catherine; Waite, Maurice; Hawker, Sara, eds. (2001). The Oxford Dictionary, Thesaurus and Wordpower Guide (Hardback) (2nd ed.). New York: Oxford University Press. ISBN 978-0-19-860373-3.
- "aught, Also ought" in Webster's Collegiate Dictionary (1927), Third Edition, Springfield, MA: G. & C. Merriam.
- "cipher", in Webster's Collegiate Dictionary (1927), Third Edition, Springfield, MA: G. & C. Merriam.
- aught at etymonline.com
- "Zero | Definition of Zero by Oxford Dictionary on Lexico.com also meaning of Zero". Lexico Dictionaries | English. Retrieved 2020-08-09.
- See:
- Douglas Harper (2011), Zero, Etymology Dictionary, Quote="figure which stands for naught in the Arabic notation," also "the absence of all quantity considered as quantity," c. 1600, from French zéro or directly from Italian zero, from Medieval Latin zephirum, from Arabic sifr "cipher," translation of Sanskrit sunya-m "empty place, desert, naught";
- Menninger, Karl (1992). Number words and number symbols: a cultural history of numbers. Courier Dover Publications. pp. 399–404. ISBN 978-0-486-27096-8.;
- "zero, n." OED Online. Oxford University Press. December 2011. Archived from the original on 7 March 2012. Retrieved 4 March 2012.
French zéro (1515 in Hatzfeld & Darmesteter) or its source Italian zero, for *zefiro, < Arabic çifr
- See:
- Smithsonian Institution, Oriental Elements of Culture in the Occident, p. 518, at Google Books, Annual Report of the Board of Regents of the Smithsonian Institution; Harvard University Archives, Quote="Sifr occurs in the meaning of "empty" even in the pre-Islamic time. ... Arabic sifr in the meaning of zero is a translation of the corresponding India sunya.";
- Jan Gullberg (1997), Mathematics: From the Birth of Numbers, W.W. Norton & Co., ISBN 978-0-393-04002-9, p. 26, Quote = Zero derives from Hindu sunya – meaning void, emptiness – via Arabic sifr, Latin cephirum, Italian zevero.;
- Robert Logan (2010), The Poetry of Physics and the Physics of Poetry, World Scientific, ISBN 978-981-4295-92-5, p. 38, Quote = "The idea of sunya and place numbers was transmitted to the Arabs who translated sunya or "leave a space" into their language as sifr."
- Zero, Merriam Webster online Dictionary
- Ifrah, Georges (2000). The Universal History of Numbers: From Prehistory to the Invention of the Computer. Wiley. ISBN 978-0-471-39340-5.
- 'Aught' definition, Dictionary.com – Retrieved April 2013.
- 'Aught' synonyms, Thesaurus.com – Retrieved April 2013.
- "Egyptian numerals". mathshistory.st-andrews.ac.uk. Retrieved 21 December 2019.
- Joseph, George Gheverghese (2011). The Crest of the Peacock: Non-European Roots of Mathematics (Third ed.). Princeton UP. p. 86. ISBN 978-0-691-13526-7.
- Kaplan, Robert. (2000). The Nothing That Is: A Natural History of Zero. Oxford: Oxford University Press.
- Diehl, p. 186
- Mortaigne, Véronique (28 November 2014). "The golden age of Mayan civilisation – exhibition review". The Guardian. Archived from the original on 28 November 2014. Retrieved 10 October 2015.
- Wallin, Nils-Bertil (19 November 2002). "The History of Zero". YaleGlobal online. The Whitney and Betty Macmillan Center for International and Area Studies at Yale. Archived from the original on 25 August 2016. Retrieved 1 September 2016.
- Huggett, Nick (2019), Zalta, Edward N. (ed.), "Zeno's Paradoxes", The Stanford Encyclopedia of Philosophy (Winter 2019 ed.), Metaphysics Research Lab, Stanford University, retrieved 2020-08-09
- Neugebauer, Otto (1969) [1957]. The Exact Sciences in Antiquity (2 ed.). Dover Publications. pp. 13–14, plate 2. ISBN 978-0-486-22332-2.
- Mercier, Raymond, "Consideration of the Greek symbol 'zero'" (PDF), Home of Kairos
- Ptolemy (1998) [1984, c.150], Ptolemy's Almagest, translated by Toomer, G. J., Princeton University Press, pp. 306–307, ISBN 0-691-00260-6
- O'Connor, J J; Robertson, E F, A history of Zero, MacTutor History of Mathematics
- Pedersen, Olaf (2010) [1974], A Survey of the Almagest, Springer, pp. 232–235, ISBN 978-0-387-84825-9
- Neugebauer, Otto (2016) [1979], Ethiopic Astronomy and Computus (Red Sea Press ed.), Red Sea Press, pp. 25, 53, 93, 183, Plate I, ISBN 978-1-56902-440-9. The pages in this edition have numbers six less than the same pages in the original edition.
- Deckers, Michael (2003) [525], Cyclus Decemnovennalis Dionysii – Nineteen Year Cycle of Dionysius, archived from the original on January 15, 2019
- C. W. Jones, ed., Opera Didascalica, vol. 123C in Corpus Christianorum, Series Latina.
- Hodgkin, Luke (2005). A History of Mathematics : From Mesopotamia to Modernity: From Mesopotamia to Modernity. Oxford University Press. p. 85. ISBN 978-0-19-152383-0.
- O'Connor, J.J. (Jan 2004). "Chinese numerals". Mac Tutor. School of Mathematics and Statistics University of St Andrews, Scotland. Retrieved 14 June 2020.
- Crossley, Lun. 1999, p. 12 "the ancient Chinese system is a place notation system"
- Kang-Shen Shen; John N. Crossley; Anthony W.C. Lun; Hui Liu (1999). The Nine Chapters on the Mathematical Art: Companion and Commentary. Oxford UP. p. 35. ISBN 978-0-19-853936-0.
zero was regarded as a number in India ... whereas the Chinese employed a vacant position
- "Mathematics in the Near and Far East" (PDF). grmath4.phpnet.us. p. 262.
- Struik, Dirk J. (1987). A Concise History of Mathematics. New York: Dover Publications. pp. 32–33. "In these matrices we find negative numbers, which appear here for the first time in history."
- Kim Plofker (2009). Mathematics in India. Princeton UP. pp. 55–56. ISBN 978-0-691-12067-6.
- Vaman Shivaram Apte (1970). Sanskrit Prosody and Important Literary and Geographical Names in the Ancient History of India. Motilal Banarsidass. pp. 648–649. ISBN 978-81-208-0045-8.
- "Math for Poets and Drummers" (PDF). people.sju.edu.
- Kim Plofker (2009), Mathematics in India, Princeton University Press, ISBN 978-0-691-12067-6, pp. 54–56. Quote – "In the Chandah-sutra of Pingala, dating perhaps the third or second century BC, [ ...] Pingala's use of a zero symbol [śūnya] as a marker seems to be the first known explicit reference to zero." Kim Plofker (2009), Mathematics in India, Princeton University Press, ISBN 978-0-691-12067-6, 55–56. "In the Chandah-sutra of Pingala, dating perhaps the third or second century BC, there are five questions concerning the possible meters for any value "n". [ ...] The answer is (2)7 = 128, as expected, but instead of seven doublings, the process (explained by the sutra) required only three doublings and two squarings – a handy time saver where "n" is large. Pingala's use of a zero symbol as a marker seems to be the first known explicit reference to zero.
- Bourbaki, Nicolas Elements of the History of Mathematics (1998), p. 46. Britannica Concise Encyclopedia (2007), entry "Algebra"
- Weiss, Ittay (20 September 2017). "Nothing matters: How India's invention of zero helped create modern mathematics". The Conversation.
- Devlin, Hannah (13 September 2017). "Much ado about nothing: ancient Indian text contains earliest zero symbol". The Guardian. ISSN 0261-3077. Retrieved 14 September 2017.
- Revell, Timothy (14 September 2017). "History of zero pushed back 500 years by ancient Indian text". New Scientist. Retrieved 25 October 2017.
- "Carbon dating finds Bakhshali manuscript contains oldest recorded origins of the symbol 'zero'". Bodleian Library. 14 September 2017. Retrieved 25 October 2017.
- Ifrah, Georges (2000), p. 416.
- Aryabhatiya of Aryabhata, translated by Walter Eugene Clark.
- O'Connor, Robertson, J.J., E.F. "Aryabhata the Elder". School of Mathematics and Statistics University of St Andrews, Scotland. Retrieved 26 May 2013.
- William L. Hosch, ed. (15 August 2010). The Britannica Guide to Numbers and Measurement (Math Explained). books.google.com.my. The Rosen Publishing Group. pp. 97–98. ISBN 978-1-61530-108-9.
- Algebra with Arithmetic of Brahmagupta and Bhaskara, translated to English by Henry Thomas Colebrooke (1817) London
- Kaplan, Robert (1999). The Nothing That Is: A Natural History of Zero. New York: Oxford University Press. pp. 68–75. ISBN 978-0-19-514237-2.
- Cœdès, Georges, "A propos de l'origine des chiffres arabes," Bulletin of the School of Oriental Studies, University of London, Vol. 6, No. 2, 1931, pp. 323–328. Diller, Anthony, "New Zeros and Old Khmer," The Mon-Khmer Studies Journal, Vol. 25, 1996, pp. 125–132.
- Casselman, Bill. "All for Nought". ams.org. University of British Columbia), American Mathematical Society.
- Ifrah, Georges (2000), p. 400.
- "Much ado about nothing: ancient Indian text contains earliest zero symbol". The Guardian. Retrieved 14 September 2017.
- Pannekoek, A. (1961). A History of Astronomy. George Allen & Unwin. p. 165.
- Will Durant (1950), The Story of Civilization, Volume 4, The Age of Faith: Constantine to Dante – A.D. 325–1300, Simon & Schuster, ISBN 978-0-9650007-5-8, p. 241, Quote = "The Arabic inheritance of science was overwhelmingly Greek, but Hindu influences ranked next. In 773, at Mansur's behest, translations were made of the Siddhantas – Indian astronomical treatises dating as far back as 425 BC; these versions may have the vehicle through which the "Arabic" numerals and the zero were brought from India into Islam. In 813, al-Khwarizmi used the Hindu numerals in his astronomical tables."
- Brezina, Corona (2006). Al-Khwarizmi: The Inventor of Algebra. The Rosen Publishing Group. ISBN 978-1-4042-0513-0.
- Will Durant (1950), The Story of Civilization, Volume 4, The Age of Faith, Simon & Schuster, ISBN 978-0-9650007-5-8, p. 241, Quote = "In 976, Muhammad ibn Ahmad, in his Keys of the Sciences, remarked that if, in a calculation, no number appears in the place of tens, a little circle should be used "to keep the rows". This circle the Mosloems called ṣifr, "empty" whence our cipher."
- Sigler, L., Fibonacci's Liber Abaci. English translation, Springer, 2003.
- Grimm, R.E., "The Autobiography of Leonardo Pisano", Fibonacci Quarterly 11/1 (February 1973), pp. 99–104.
- Hansen, Alice (2008-06-09). Primary Mathematics: Extending Knowledge in Practice. SAGE. ISBN 978-0-85725-233-3.
- Lemma B.2.2, The integer 0 is even and is not odd, in Penner, Robert C. (1999). Discrete Mathematics: Proof Techniques and Mathematical Structures. World Scientific. p. 34. ISBN 978-981-02-4088-2.
- W., Weisstein, Eric. "Zero". mathworld.wolfram.com. Retrieved 4 April 2018.
- Bunt, Lucas Nicolaas Hendrik; Jones, Phillip S.; Bedient, Jack D. (1976). The historical roots of elementary mathematics. Courier Dover Publications. pp. 254–255. ISBN 978-0-486-13968-5., Extract of pp. 254–255
- Reid, Constance (1992). From zero to infinity: what makes numbers interesting (4th ed.). Mathematical Association of America. p. 23. ISBN 978-0-88385-505-8.
zero neither prime nor composite.
- Wu, X.; Ichikawa, T.; Cercone, N. (25 October 1996). Knowledge-Base Assisted Database Retrieval Systems. World Scientific. ISBN 978-981-4501-75-0.
- Chris Woodford 2006, p. 9.
- Paul DuBois. "MySQL Cookbook: Solutions for Database Developers and Administrators" 2014. p. 204.
- Arnold Robbins; Nelson Beebe. "Classic Shell Scripting". 2005. p. 274
- Iztok Fajfar. "Start Programming Using HTML, CSS, and JavaScript". 2015. p. 160.
- Darren R. Hayes. "A Practical Guide to Computer Forensics Investigations". 2014. p. 399
- Bemer, R. W. (1967). "Towards standards for handwritten zero and oh: much ado about nothing (and a letter), or a partial dossier on distinguishing between handwritten zero and oh". Communications of the ACM. 10 (8): 513–518. doi:10.1145/363534.363563.
- Steel, Duncan (2000). Marking time: the epic quest to invent the perfect calendar. John Wiley & Sons. p. 113. ISBN 978-0-471-29827-4.
In the B.C./A.D. scheme there is no year zero. After 31 December 1 BC came 1 January AD 1. ... If you object to that no-year-zero scheme, then don't use it: use the astronomer's counting scheme, with negative year numbers.
Bibliography
- Amir D. Aczel (2015) Finding Zero, New York City: Palgrave Macmillan. ISBN 978-1-137-27984-2
- Barrow, John D. (2001) The Book of Nothing, Vintage. ISBN 0-09-928845-1.
- Diehl, Richard A. (2004) The Olmecs: America's First Civilization, Thames & Hudson, London.
- Ifrah, Georges (2000) The Universal History of Numbers: From Prehistory to the Invention of the Computer, Wiley. ISBN 0-471-39340-1.
- Kaplan, Robert (2000) The Nothing That Is: A Natural History of Zero, Oxford: Oxford University Press.
- Seife, Charles (2000) Zero: The Biography of a Dangerous Idea, Penguin USA (Paper). ISBN 0-14-029647-6.
- Bourbaki, Nicolas (1998). Elements of the History of Mathematics. Berlin, Heidelberg, and New York: Springer-Verlag. ISBN 3-540-64767-8.
- Isaac Asimov (1978). Article "Nothing Counts" in Asimov on Numbers. Pocket Books.
- This article is based on material taken from the Free On-line Dictionary of Computing prior to 1 November 2008 and incorporated under the "relicensing" terms of the GFDL, version 1.3 or later.
- Chris Woodford (2006), Digital Technology, Evans Brothers, ISBN 978-0-237-52725-9
External links
| Wikimedia Commons has media related to 0 (number). |
| Look up zero in Wiktionary, the free dictionary. |
| Wikiquote has quotations related to: Zero |
- Searching for the World’s First Zero
- A History of Zero
- Zero Saga
- The History of Algebra
- Edsger W. Dijkstra: Why numbering should start at zero, EWD831 (PDF of a handwritten manuscript)
- Zero on In Our Time at the BBC
- Weisstein, Eric W. "0". MathWorld.

- "Zero". Encyclopædia Britannica (11th ed.). 1911.
- "Zero". Encyclopedia Americana. 1920.