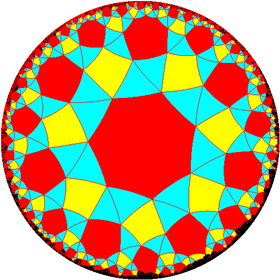
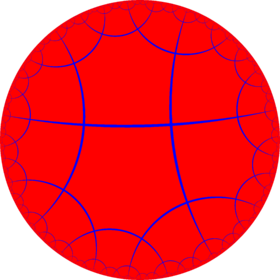
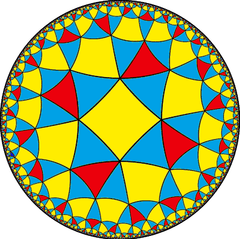
Snub tetrahexagonal tiling
In geometry, the snub tetrahexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of sr{6,4}.
| Snub tetrahexagonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 3.3.4.3.6 |
| Schläfli symbol | sr{6,4} or |
| Wythoff symbol | | 6 4 2 |
| Coxeter diagram |      |
| Symmetry group | [6,4]+, (642) |
| Dual | Order-6-4 floret pentagonal tiling |
| Properties | Vertex-transitive Chiral |
Images
Drawn in chiral pairs, with edges missing between black triangles:
Related polyhedra and tiling
The snub tetrahexagonal tiling is fifth in a series of snub polyhedra and tilings with vertex figure 3.3.4.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
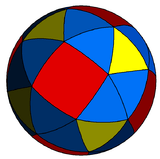
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub figures |
 |
 |
 |
 |
|
 |
 |
 |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Gyro figures |
 |
 |
 |
 |
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
| Uniform tetrahexagonal tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,4], (*642) (with [6,6] (*662), [(4,3,3)] (*443) , [∞,3,∞] (*3222) index 2 subsymmetries) (And [(∞,3,∞,3)] (*3232) index 4 subsymmetry) | |||||||||||
  =    =   =  |
=  |
= =  = |
= |
=  = =  |
= |
| |||||
 |
 |
 |
 |
 |
 |
 | |||||
| {6,4} | t{6,4} | r{6,4} | t{4,6} | {4,6} | rr{6,4} | tr{6,4} | |||||
| Uniform duals | |||||||||||
 |
|
|
|
|
|
| |||||
 |
 |
 |
 |
 |
 |
 | |||||
| V64 | V4.12.12 | V(4.6)2 | V6.8.8 | V46 | V4.4.4.6 | V4.8.12 | |||||
| Alternations | |||||||||||
| [1+,6,4] (*443) |
[6+,4] (6*2) |
[6,1+,4] (*3222) |
[6,4+] (4*3) |
[6,4,1+] (*662) |
[(6,4,2+)] (2*32) |
[6,4]+ (642) | |||||
 =  |
=   |
=   |
= |
=  |
=  |
| |||||
 |
 |
 |
 |
 |
 |
| |||||
| h{6,4} | s{6,4} | hr{6,4} | s{4,6} | h{4,6} | hrr{6,4} | sr{6,4} | |||||
gollark: I fear it.
gollark: The very ominously named "online safety bill" is very ominous and would impose ridiculous compliance requirements on basically everything, as well as allowing the media regulator to block sites which don't comply, as well as in a plausibly-deniable way banning end to end encryption, as well as requiring all web platform things to censor "harmful content".
gollark: The UK is also doing bad things nominally but not really in opposition to technology companies.
gollark: Australis is doing rather bad things seemingly not driven by and not desired by any tech companies.
gollark: Much of that seems to be from governments now.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
See also
 |
Wikimedia Commons has media related to Uniform tiling 3-3-4-3-6. |
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
  | ||||||
| ||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.