Domino tiling

In geometry, a domino tiling of a region in the Euclidean plane is a tessellation of the region by dominos, shapes formed by the union of two unit squares meeting edge-to-edge. Equivalently, it is a perfect matching in the grid graph formed by placing a vertex at the center of each square of the region and connecting two vertices when they correspond to adjacent squares.

A domino tiling of an 8×8 square

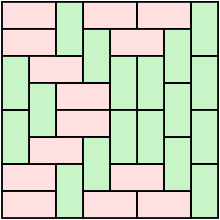
Height functions

For some classes of tilings on a regular grid in two dimensions, it is possible to define a height function associating an integer to the vertices of the grid. For instance, draw a chessboard, fix a node ${\displaystyle A_{0}}$ with height 0, then for any node there is a path from ${\displaystyle A_{0}}$ to it. On this path define the height of each node ${\displaystyle A_{n+1}}$ (i.e. corners of the squares) to be the height of the previous node ${\displaystyle A_{n}}$ plus one if the square on the right of the path from ${\displaystyle A_{n}}$ to ${\displaystyle A_{n+1}}$ is black, and minus one otherwise.

More details can be found in Kenyon & Okounkov (2005).

Thurston's height condition

William Thurston (1990) describes a test for determining whether a simply-connected region, formed as the union of unit squares in the plane, has a domino tiling. He forms an undirected graph that has as its vertices the points (x,y,z) in the three-dimensional integer lattice, where each such point is connected to four neighbors: if x + y is even, then (x,y,z) is connected to (x + 1,y,z + 1), (x − 1,y,z + 1), (x,y + 1,z − 1), and (x,y − 1,z − 1), while if x + y is odd, then (x,y,z) is connected to (x + 1,y,z − 1), (x − 1,y,z − 1), (x,y + 1,z + 1), and (x,y − 1,z + 1). The boundary of the region, viewed as a sequence of integer points in the (x,y) plane, lifts uniquely (once a starting height is chosen) to a path in this three-dimensional graph. A necessary condition for this region to be tileable is that this path must close up to form a simple closed curve in three dimensions, however, this condition is not sufficient. Using more careful analysis of the boundary path, Thurston gave a criterion for tileability of a region that was sufficient as well as necessary.

Counting tilings of regions

A domino tiling of an 8×8 square using the minimum number of long-edge-to-long-edge pairs (1 pair in the center). This arrangement is also a valid Tatami tiling of an 8x8 square, with no four dominoes touching at an internal point.

The number of ways to cover an ${\displaystyle m\times n}$ rectangle with ${\displaystyle {\frac {mn}{2}}}$ dominoes, calculated independently by Temperley & Fisher (1961) and Kasteleyn (1961), is given by

${\displaystyle \prod _{j=1}^{\lceil {\frac {m}{2}}\rceil }\prod _{k=1}^{\lceil {\frac {n}{2}}\rceil }\left(4\cos ^{2}{\frac {\pi j}{m+1}}+4\cos ^{2}{\frac {\pi k}{n+1}}\right).}$

When both m and n are odd, the formula correctly reduces to zero possible domino tilings.

A special case occurs when tiling the ${\displaystyle 2\times n}$ rectangle with n dominoes: the sequence reduces to the Fibonacci sequence (sequence A000045 in the OEIS) (Klarner & Pollack 1980) harv error: no target: CITEREFKlarnerPollack1980 (help).

Another special case happens for squares with m = n = 0, 2, 4, 6, 8, 10, 12, ... is

1, 2, 36, 6728, 12988816, 258584046368, 53060477521960000, ... (sequence A004003 in the OEIS).

These numbers can be found by writing them as the Pfaffian of an ${\displaystyle mn\times mn}$ skew-symmetric matrix whose eigenvalues can be found explicitly. This technique may be applied in many mathematics-related subjects, for example, in the classical, 2-dimensional computation of the dimer-dimer correlator function in statistical mechanics.

The number of tilings of a region is very sensitive to boundary conditions, and can change dramatically with apparently insignificant changes in the shape of the region. This is illustrated by the number of tilings of an Aztec diamond of order n, where the number of tilings is 2^(n + 1)n/2. If this is replaced by the "augmented Aztec diamond" of order n with 3 long rows in the middle rather than 2, the number of tilings drops to the much smaller number D(n,n), a Delannoy number, which has only exponential rather than super-exponential growth in n. For the "reduced Aztec diamond" of order n with only one long middle row, there is only one tiling.

• 
  An Aztec diamond of order 4, which has 1024 domino tilings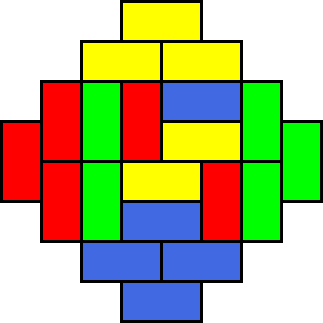
• 
  One possible tiling

Tatami

Tatami are Japanese floor mats in the shape of a domino (1x2 rectangle). They are used to tile rooms, but with additional rules about how they may be placed. In particular, typically, junctions where three tatami meet are considered auspicious, while junctions where four meet are inauspicious, so a proper tatami tiling is one where only three tatami meet at any corner (Mathar 2013; Ruskey & Woodcock 2009). The problem of tiling an irregular room by tatami that meet three to a corner is NP-complete (Erickson & Ruskey 2013).

Degenerated space-filling curves

Any finite set of cells forming regular square grid n×n can be indexed by a selected Space-filling curve that is consistent with squares (that do a recursive four-partition of the quadrilateral unit grid), with an index i ranging from 0 to n²-1. Geometrically, the curve can be drawn as a path through the center of the square cells. A domino tiling is obtained by merging neighboring cells. The index j of each domino will be obtained by the function j=floor(i ÷ 2) of the original grid index. The new fractal curve is a "degenerated curve" because is another fractal. Examples:

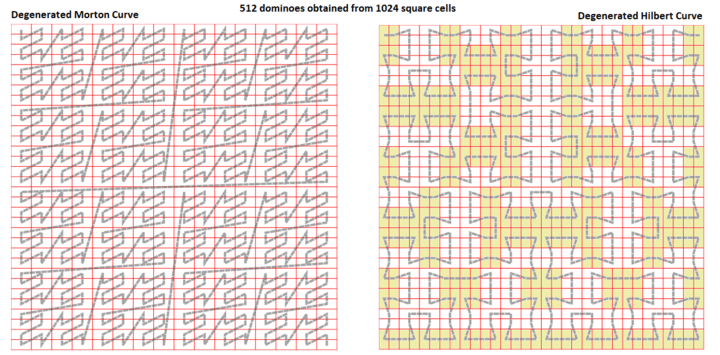
The "degenerated Morton space-filling curve" produces a regular horizontal-oriented domino tiling; the curve is related with Geohash indexing, where the Z-shape curve is transformed into a И-shape curve.

The "degenerated Hilbert space-filling curve" produces an aperiodic tiling system, mixing horizontal- and vertical-oriented dominoes, 50% of each orientation. The degenerated Hilbert curve is isomorphic to the Munkres's fractal.[1]

See also

• Gaussian free field, the scaling limit of the height function in the generic situation (e.g., inside the inscribed disk of a large aztec diamond)
• Mutilated chessboard problem, a puzzle concerning domino tiling of a 62-square subset of the chessboard
• Statistical mechanics

References

1. The Munkres's fractal is defined at "Theorem 44.1" in faculty.etsu.edu/gardnerr/5357/notes/Munkres-44

• Bodini, Olivier; Latapy, Matthieu (2003), "Generalized Tilings with Height Functions" (PDF), Morfismos, 7 (1): 47–68, ISSN 1870-6525, archived from the original on 2012-02-10, retrieved 2008-09-08CS1 maint: unfit url (link)
• Erickson, Alejandro; Ruskey, Frank (2013), "Domino tatami covering is NP-complete", Combinatorial algorithms, Lecture Notes in Comput. Sci., 8288, Springer, Heidelberg, pp. 140–149, arXiv:1305.6669, doi:10.1007/978-3-642-45278-9_13, MR 3162068
• Faase, F. (1998), "On the number of specific spanning subgraphs of the graphs G X P_n", Ars Combin., 49: 129–154, MR 1633083
• Hock, J. L.; McQuistan, R. B. (1984), "A note on the occupational degeneracy for dimers on a saturated two-dimenisonal lattice space", Discrete Applied Mathematics, 8: 101–104, doi:10.1016/0166-218X(84)90083-0, MR 0739603
• Kasteleyn, P. W. (1961), "The statistics of dimers on a lattice. I. The number of dimer arrangements on a quadratic lattice", Physica, 27 (12): 1209–1225, Bibcode:1961Phy....27.1209K, doi:10.1016/0031-8914(61)90063-5
• Kenyon, Richard (2000), "The planar dimer model with boundary: a survey", in Baake, Michael; Moody, Robert V. (eds.), Directions in mathematical quasicrystals, CRM Monograph Series, 13, Providence, RI: American Mathematical Society, pp. 307–328, ISBN 0-8218-2629-8, MR 1798998, Zbl 1026.82007
• Kenyon, Richard; Okounkov, Andrei (2005), "What is … a dimer?" (PDF), Notices of the American Mathematical Society, 52 (3): 342–343, ISSN 0002-9920
• Klarner, David; Pollack, Jordan (1980), "Domino tilings of rectangles with fixed width", Discrete Mathematics, 32 (1): 45–52, doi:10.1016/0012-365X(80)90098-9, MR 0588907, Zbl 0444.05009
• Mathar, Richard J. (2013), Paving rectangular regions with rectangular tiles: tatami and non-tatami tilings, arXiv:1311.6135, Bibcode:2013arXiv1311.6135M
• Propp, James (2005), "Lambda-determinants and domino-tilings", Advances in Applied Mathematics, 34 (4): 871–879, arXiv:math.CO/0406301, doi:10.1016/j.aam.2004.06.005
• Ruskey, Frank; Woodcock, Jennifer (2009), "Counting fixed-height Tatami tilings", Electronic Journal of Combinatorics, 16 (1): R126, MR 2558263
• Sellers, James A. (2002), "Domino tilings and products of Fibonacci and Pell numbers", Journal of Integer Sequences, 5 (Article 02.1.2)
• Stanley, Richard P. (1985), "On dimer coverings of rectangles of fixed width", Discrete Applied Mathematics, 12: 81–87, doi:10.1016/0166-218x(85)90042-3, MR 0798013
• Thurston, W. P. (1990), "Conway's tiling groups", American Mathematical Monthly, Mathematical Association of America, 97 (8): 757–773, doi:10.2307/2324578, JSTOR 2324578
• Wells, David (1997), The Penguin Dictionary of Curious and Interesting Numbers (revised ed.), London: Penguin, p. 182, ISBN 0-14-026149-4
• Temperley, H. N. V.; Fisher, Michael E. (1961), "Dimer problem in statistical mechanics – an exact result", Philosophical Magazine, 6 (68): 1061–1063, doi:10.1080/14786436108243366