Order-4 apeirogonal tiling

In geometry, the order-4 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,4}.

Order-4 apeirogonal tiling
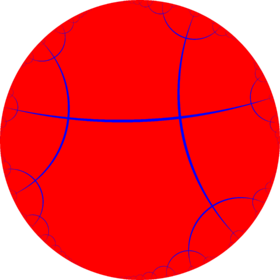Poincaré disk model of the hyperbolic plane
Type	Hyperbolic regular tiling
Vertex configuration	∞^4
Schläfli symbol	{∞,4} r{∞,∞} t(∞,∞,∞) t0,1,2,3(∞,∞,∞,∞)
Wythoff symbol	4 | ∞ 2 2 | ∞ ∞ ∞ ∞ | ∞
Coxeter diagram
Symmetry group	[∞,4], (*∞42) [∞,∞], (*∞∞2) [(∞,∞,∞)], (*∞∞∞) (*∞∞∞∞)
Dual	Infinite-order square tiling
Properties	Vertex-transitive, edge-transitive, face-transitive edge-transitive

Symmetry

This tiling represents the mirror lines of *2^∞ symmetry. It dual to this tiling represents the fundamental domains of orbifold notation *∞∞∞∞ symmetry, a square domain with four ideal vertices.

Uniform colorings

Like the Euclidean square tiling there are 9 uniform colorings for this tiling, with 3 uniform colorings generated by triangle reflective domains. A fourth can be constructed from an infinite square symmetry (*∞∞∞∞) with 4 colors around a vertex. The checker board, r{∞,∞}, coloring defines the fundamental domains of [(∞,4,4)], (*∞44) symmetry, usually shown as black and white domains of reflective orientations.

1 color	2 color	3 and 2 colors		4, 3 and 2 colors
[∞,4], (*∞42)	[∞,∞], (*∞∞2)	[(∞,∞,∞)], (*∞∞∞)		(*∞∞∞∞)
{∞,4}	r{∞,∞} = {∞,4}​^1⁄2	t0,2(∞,∞,∞) = r{∞,∞}​^1⁄2		t0,1,2,3(∞,∞,∞,∞) = r{∞,∞}​^1⁄4 = {∞,4}​^1⁄8
(1111)	(1212)	(1213)	(1112)	(1234)	(1123)	(1122)
	=	= =		= =

Related polyhedra and tiling

This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,4}, and Coxeter diagram , with n progressing to infinity.

*n42 symmetry mutation of regular tilings: {n,4}
Spherical		Euclidean	Hyperbolic tilings
2^4	3^4	4^4	5^4	6^4	7^4	8^4	...∞^4

Paracompact uniform tilings in [∞,4] family
{∞,4}	t{∞,4}	r{∞,4}	2t{∞,4}=t{4,∞}	2r{∞,4}={4,∞}	rr{∞,4}	tr{∞,4}
Dual figures
V∞^4	V4.∞.∞	V(4.∞)^2	V8.8.∞	V4^∞	V4^3.∞	V4.8.∞
Alternations
[1^+,∞,4] (*44∞)	[∞^+,4] (∞*2)	[∞,1^+,4] (*2∞2∞)	[∞,4^+] (4*∞)	[∞,4,1^+] (*∞∞2)	[(∞,4,2^+)] (2*2∞)	[∞,4]^+ (∞42)
=				=
h{∞,4}	s{∞,4}	hr{∞,4}	s{4,∞}	h{4,∞}	hrr{∞,4}	s{∞,4}
Alternation duals
V(∞.4)^4	V3.(3.∞)^2	V(4.∞.4)^2	V3.∞.(3.4)^2	V∞^∞	V∞.4^4	V3.3.4.3.∞

Paracompact uniform tilings in [∞,∞] family
= =	= =	= =	= =	= =	=	=
{∞,∞}	t{∞,∞}	r{∞,∞}	2t{∞,∞}=t{∞,∞}	2r{∞,∞}={∞,∞}	rr{∞,∞}	tr{∞,∞}
Dual tilings
V∞^∞	V∞.∞.∞	V(∞.∞)^2	V∞.∞.∞	V∞^∞	V4.∞.4.∞	V4.4.∞
Alternations
[1^+,∞,∞] (*∞∞2)	[∞^+,∞] (∞*∞)	[∞,1^+,∞] (*∞∞∞∞)	[∞,∞^+] (∞*∞)	[∞,∞,1^+] (*∞∞2)	[(∞,∞,2^+)] (2*∞∞)	[∞,∞]^+ (2∞∞)
h{∞,∞}	s{∞,∞}	hr{∞,∞}	s{∞,∞}	h2{∞,∞}	hrr{∞,∞}	sr{∞,∞}
Alternation duals
V(∞.∞)^∞	V(3.∞)^3	V(∞.4)^4	V(3.∞)^3	V∞^∞	V(4.∞.4)^2	V3.3.∞.3.∞

Paracompact uniform tilings in [(∞,∞,∞)] family
(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) h2{∞,∞}	(∞,∞,∞) h{∞,∞}	r(∞,∞,∞) r{∞,∞}	t(∞,∞,∞) t{∞,∞}
Dual tilings
V∞^∞	V∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞	V∞^∞	V∞.∞.∞.∞	V∞.∞.∞
Alternations
[(1^+,∞,∞,∞)] (*∞∞∞∞)	[∞^+,∞,∞)] (∞*∞)	[∞,1^+,∞,∞)] (*∞∞∞∞)	[∞,∞^+,∞)] (∞*∞)	[(∞,∞,∞,1^+)] (*∞∞∞∞)	[(∞,∞,∞^+)] (∞*∞)	[∞,∞,∞)]^+ (∞∞∞)
Alternation duals
V(∞.∞)^∞	V(∞.4)^4	V(∞.∞)^∞	V(∞.4)^4	V(∞.∞)^∞	V(∞.4)^4	V3.∞.3.∞.3.∞

See also

• Tilings of regular polygons
• List of uniform planar tilings
• List of regular polytopes

References

• John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
• "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.

External links

• Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
• Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
• Hyperbolic and Spherical Tiling Gallery
• KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
• Hyperbolic Planar Tessellations, Don Hatch