Order-5 square tiling
In geometry, the order-5 square tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {4,5}.
| Order-5 square tiling | |
|---|---|
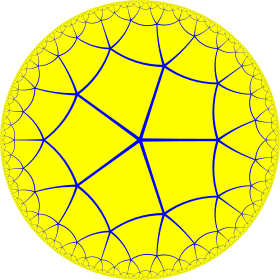 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | 45 |
| Schläfli symbol | {4,5} |
| Wythoff symbol | 5 | 4 2 |
| Coxeter diagram |     |
| Symmetry group | [5,4], (*542) |
| Dual | Order-4 pentagonal tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive |
Related polyhedra and tiling
| Spherical | Hyperbolic tilings | |||||||
|---|---|---|---|---|---|---|---|---|
 {2,5}  |
 {3,5}  |
{4,5} |
 {5,5} |
 {6,5}  |
 {7,5}  |
 {8,5}  |
... |  {∞,5}  |
This tiling is topologically related as a part of sequence of regular polyhedra and tilings with vertex figure (4n).
| *n42 symmetry mutation of regular tilings: {4,n} | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Compact hyperbolic | Paracompact | ||||||||
 {4,3} |
 {4,4} |
{4,5} |
 {4,6} |
 {4,7} |
 {4,8}... |
 {4,∞} | |||||
| Uniform pentagonal/square tilings | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [5,4], (*542) | [5,4]+, (542) | [5+,4], (5*2) | [5,4,1+], (*552) | ||||||||
|
|
|
|
|
|
|
 |
|
| ||
 |
 |
 |
 |
|
 |
 |
 |
 |
 | ||
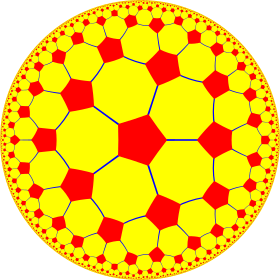| {5,4} | t{5,4} | r{5,4} | 2t{5,4}=t{4,5} | 2r{5,4}={4,5} | rr{5,4} | tr{5,4} | sr{5,4} | s{5,4} | h{4,5} | ||
| Uniform duals | |||||||||||
 |
|
|
|
|
|
|
 |
|
| ||
|
 |
 |
 |
|
 |
 |
 |
 | |||
| V54 | V4.10.10 | V4.5.4.5 | V5.8.8 | V45 | V4.4.5.4 | V4.8.10 | V3.3.4.3.5 | V3.3.5.3.5 | V55 | ||
This hyperbolic tiling is related to a semiregular infinite skew polyhedron with the same vertex figure in Euclidean 3-space.
gollark: They said they had a cable.
gollark: They have to split time on their radios between backhaul and actually serving clients, so you get horrible performance.
gollark: Do NOT range extenders, for various reasons.
gollark: OpenWRT is quite pleasant to use, in my experience.
gollark: You probably want to either have something which is explicitly an access point, or run custom firmware, because some "router" products might try and be too smart and operate a NAT.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
See also
 |
Wikimedia Commons has media related to Order-5 square tiling. |
- Square tiling
- Uniform tilings in hyperbolic plane
- List of regular polytopes
- Medial rhombic triacontahedron
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
  | ||||||
| ||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.