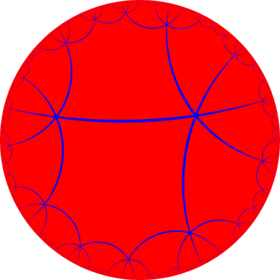
Truncated order-6 hexagonal tiling
In geometry, the truncated order-6 hexagonal tiling is a uniform tiling of the hyperbolic plane. It has Schläfli symbol of t{6,6}. It can also be identically constructed as a cantic order-6 square tiling, h2{4,6}
| Truncated order-6 hexagonal tiling | |
|---|---|
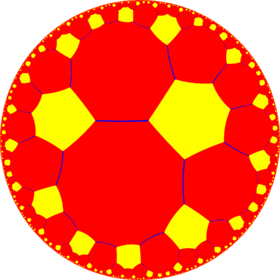 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | 6.12.12 |
| Schläfli symbol | t{6,6} or h2{4,6} t(6,6,3) |
| Wythoff symbol | 2 6 | 6 3 6 6 | |
| Coxeter diagram |         |
| Symmetry group | [6,6], (*662) [(6,6,3)], (*663) |
| Dual | Order-6 hexakis hexagonal tiling |
| Properties | Vertex-transitive |
Uniform colorings
By *663 symmetry, this tiling can be constructed as an omnitruncation, t{(6,6,3)}:
Symmetry
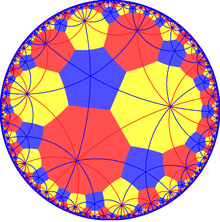
Truncated order-6 hexagonal tiling with *663 mirror lines
The dual to this tiling represent the fundamental domains of [(6,6,3)] (*663) symmetry. There are 3 small index subgroup symmetries constructed from [(6,6,3)] by mirror removal and alternation. In these images fundamental domains are alternately colored black and white, and mirrors exist on the boundaries between colors.
The symmetry can be doubled as 662 symmetry by adding a mirror bisecting the fundamental domain.
| Index | 1 | 2 | 6 | |
|---|---|---|---|---|
| Diagram |  |
 |
 |
 |
| Coxeter (orbifold) |
[(6,6,3)] =   (*663) |
[(6,1+,6,3)] =   (*3333) |
[(6,6,3+)] =  (3*33) |
[(6,6,3*)] =   (*333333) |
| Direct subgroups | ||||
| Index | 2 | 4 | 12 | |
| Diagram |  |
 |
 | |
| Coxeter (orbifold) |
[(6,6,3)]+ =  (663) |
[(6,6,3+)]+ = (3333) |
[(6,6,3*)]+ = (333333) | |
Related polyhedra and tiling
| Uniform hexahexagonal tilings | ||||||
|---|---|---|---|---|---|---|
| Symmetry: [6,6], (*662) | ||||||
  = |
= |
 = |
 = |
= |
 = |
= |
 |
|
 |
 |
 |
 |
 |
| {6,6} = h{4,6} |
t{6,6} = h2{4,6} |
r{6,6} {6,4} |
t{6,6} = h2{4,6} |
{6,6} = h{4,6} |
rr{6,6} r{6,4} |
tr{6,6} t{6,4} |
| Uniform duals | ||||||
 |
|
|
|
|
|
|
 |
 |
 |
 |
 |
 |
 |
| V66 | V6.12.12 | V6.6.6.6 | V6.12.12 | V66 | V4.6.4.6 | V4.12.12 |
| Alternations | ||||||
| [1+,6,6] (*663) |
[6+,6] (6*3) |
[6,1+,6] (*3232) |
[6,6+] (6*3) |
[6,6,1+] (*663) |
[(6,6,2+)] (2*33) |
[6,6]+ (662) |
 |
 |
|
|
 |
|
|
|
|
|
|
|
|
|
 |
 |
|
 |
 | ||
| h{6,6} | s{6,6} | hr{6,6} | s{6,6} | h{6,6} | hrr{6,6} | sr{6,6} |
gollark: Less vaguely, laptops/desktops or other discrete computer-type things will begin to (continue to, actually?) decline as people begin using phones with better dockable IO.
gollark: More vague predictions: computers will generally get faster, but also half the computing power will end up wasted on increasingly flashy animations, poorly programmed applications, and other random nonsense like that.
gollark: Okay, no response right now.
gollark: ?remind 5y "hello future"
gollark: I may or may not have *a* closed timelike curve, but you can only send information that way.
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
See also
- Square tiling
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
  | ||||||
| ||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.