Tetragonal trapezohedron
The tetragonal trapezohedron, or deltohedron, is the second in an infinite series of face-uniform polyhedra, which are dual to the antiprisms. It has eight faces, which are congruent kites, and is dual to the square antiprism.
| Tetragonal trapezohedron | |
|---|---|
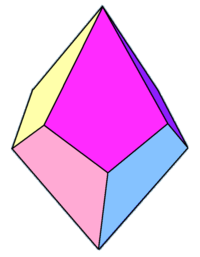 Click on picture for large version. | |
| Type | trapezohedra |
| Conway | dA4 |
| Coxeter diagram | |
| Faces | 8 kites |
| Edges | 16 |
| Vertices | 10 |
| Face configuration | V4.3.3.3 |
| Symmetry group | D4d, [2+,8], (2*4), order 16 |
| Rotation group | D4, [2,4]+, (224), order 8 |
| Dual polyhedron | Square antiprism |
| Properties | convex, face-transitive |
In mesh generation
This shape has been used as a test case for hexahedral mesh generation,[1][2][3][4][5] simplifying an earlier test case posited by mathematician Robert Schneiders in the form of a square pyramid with its boundary subdivided into 16 quadrilaterals. In this context the tetragonal trapezohedron has also been called the cubical octahedron,[3] quadrilateral octahedron,[4] or octagonal spindle,[5] because it has eight quadrilateral faces and is uniquely defined as a combinatorial polyhedron by that property.[3] Adding four cuboids to a mesh for the cubical octahedron would also give a mesh for Schneiders' pyramid.[2] As a simply-connected polyhedron with an even number of quadrilateral faces, the cubical octahedron can be decomposed into topological cuboids with curved faces that meet face-to-face without subdividing the boundary quadrilaterals,[1][5][6] and an explicit mesh of this type has been constructed.[4] However, it is unclear whether a decomposition of this type can be obtained in which all the cuboids are convex polyhedra with flat faces.[1][5]
Related polyhedra
| Family of trapezohedra Vn.3.3.3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron |  |
 |
 |
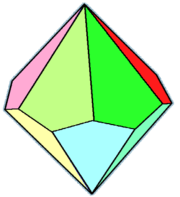 |
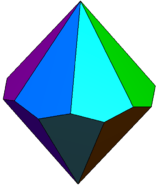 |
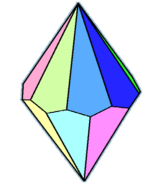 |
 |
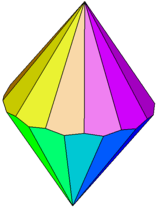 |
|||
| Tiling |  |
 |
 |
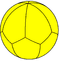 |
 |
 |
 |
 |
|||
| Config. | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
The tetragonal trapezohedron is first in a series of dual snub polyhedra and tilings with face configuration V3.3.4.3.n.
| 4n2 symmetry mutations of snub tilings: 3.3.4.3.n | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry 4n2 |
Spherical | Euclidean | Compact hyperbolic | Paracomp. | ||||
| 242 | 342 | 442 | 542 | 642 | 742 | 842 | ∞42 | |
| Snub figures |
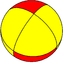 |
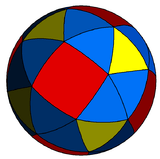 |
 |
 |
 |
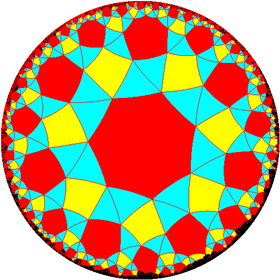 |
 |
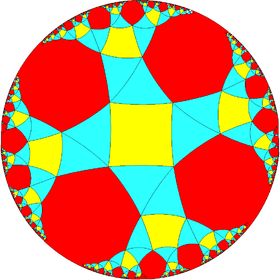 |
| Config. | 3.3.4.3.2 | 3.3.4.3.3 | 3.3.4.3.4 | 3.3.4.3.5 | 3.3.4.3.6 | 3.3.4.3.7 | 3.3.4.3.8 | 3.3.4.3.∞ |
| Gyro figures |
 |
 |
 |
 |
||||
| Config. | V3.3.4.3.2 | V3.3.4.3.3 | V3.3.4.3.4 | V3.3.4.3.5 | V3.3.4.3.6 | V3.3.4.3.7 | V3.3.4.3.8 | V3.3.4.3.∞ |
References
- Eppstein, David (1996), "Linear complexity hexahedral mesh generation", Proceedings of the Twelfth Annual Symposium on Computational Geometry (SCG '96), New York, NY, USA: ACM, pp. 58–67, arXiv:cs/9809109, doi:10.1145/237218.237237, MR 1677595.
- Mitchell, S. A. (1999), "The all-hex geode-template for conforming a diced tetrahedral mesh to any diced hexahedral mesh", Engineering with Computers, 15 (3): 228–235, doi:10.1007/s003660050018.
- Schwartz, Alexander; Ziegler, Günter M. (2004), "Construction techniques for cubical complexes, odd cubical 4-polytopes, and prescribed dual manifolds", Experimental Mathematics, 13 (4): 385–413, doi:10.1080/10586458.2004.10504548, MR 2118264.
- Carbonera, Carlos D.; Shepherd, Jason F.; Shepherd, Jason F. (2006), "A constructive approach to constrained hexahedral mesh generation", Proceedings of the 15th International Meshing Roundtable, Berlin: Springer, pp. 435–452, doi:10.1007/978-3-540-34958-7_25.
- Erickson, Jeff (2013), "Efficiently hex-meshing things with topology", Proceedings of the Twenty-ninth Annual Symposium on Computational Geometry (SoCG '13) (PDF), New York, NY, USA: ACM, pp. 37–46, doi:10.1145/2462356.2462403.
- Mitchell, Scott A. (1996), "A characterization of the quadrilateral meshes of a surface which admit a compatible hexahedral mesh of the enclosed volume", STACS 96: 13th Annual Symposium on Theoretical Aspects of Computer Science Grenoble, France, February 22–24, 1996, Proceedings, Lecture Notes in Computer Science, 1046, Berlin: Springer, pp. 465–476, doi:10.1007/3-540-60922-9_38, MR 1462118.