Pentaapeirogonal tiling
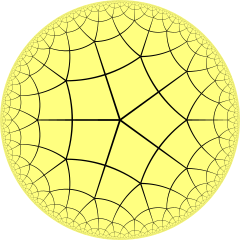
In geometry, the pentaapeirogonal tiling is a uniform tiling of the hyperbolic plane with a Schläfli symbol of r{∞,5}.
| pentaapeirogonal tiling | |
|---|---|
 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic uniform tiling |
| Vertex configuration | (5.∞)2 |
| Schläfli symbol | r{∞,5} or |
| Wythoff symbol | 2 | ∞ 5 |
| Coxeter diagram |       |
| Symmetry group | [∞,5], (*∞52) |
| Dual | Order-5-infinite rhombille tiling |
| Properties | Vertex-transitive edge-transitive |
Related polyhedra and tiling
| *5n2 symmetry mutations of quasiregular tilings: (5.n)2 | ||||||||
|---|---|---|---|---|---|---|---|---|
| Symmetry *5n2 [n,5] |
Spherical | Hyperbolic | Paracompact | Noncompact | ||||
| *352 [3,5] |
*452 [4,5] |
*552 [5,5] |
*652 [6,5] |
*752 [7,5] |
*852 [8,5]... |
*∞52 [∞,5] |
[ni,5] | |
| Figures |  |
 |
 |
 |
 |
 |
|
|
| Config. | (5.3)2 | (5.4)2 | (5.5)2 | (5.6)2 | (5.7)2 | (5.8)2 | (5.∞)2 | (5.ni)2 |
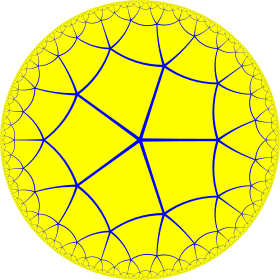
| Rhombic figures |
 |
 |
 |
 |
||||
| Config. | V(5.3)2 | V(5.4)2 | V(5.5)2 | V(5.6)2 | V(5.7)2 | V(5.8)2 | V(5.∞)2 | V(5.∞)2 |
gollark: I mean, at any given time, *can* you expect someone to have a specific 4/5-letter code?
gollark: I can't even really send off eggs to people with slots, because the ones I have blocking me right now are incubated... yay.
gollark: Yes, variations happen, but really who cares, those are statistical anomalies.
gollark: ... golds?
gollark: Usually.
See also
 |
Wikimedia Commons has media related to Uniform tiling 5-i-5-i. |
- List of uniform planar tilings
- Tilings of regular polygons
- Uniform tilings in hyperbolic plane
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
  | ||||||
| ||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.