Carrying capacity

The carrying capacity of an environment is the maximum population size of a biological species that can be sustained in that specific environment, given the food, habitat, water, and other resources available. In population ecology, carrying capacity is defined as the environment's maximal load, which is different from the concept of population equilibrium, which may be far below an environment's carrying capacity.[1] The effect of carrying capacity on population dynamics may be modelled with a logistic function.

The specific reason why a population stops growing is known as a limiting or regulating factor.

Reaching carrying capacity through a logistic growth curve

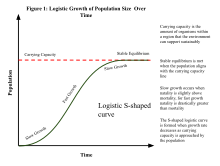
The difference between the birth rate and the death rate is the "natural increase". If the population of a given organism is below the carrying capacity of a given environment, this environment could support a positive natural increase; should it find itself above that threshold the population typically decrease. Thus, the carrying capacity is the maximum number of individuals of a species that an environment can support.

Population size decreases above carrying capacity due to a range of factors depending on the species concerned, but can include insufficient space, food supply, or sunlight. The carrying capacity of an environment may vary for different species.

Carrying capacity was originally used to determine the number of animals that could graze on a segment of land. The idea has recently been applied to humans in the context of environmentalism.[2] For the human population variables such as sanitation and medical care are sometimes considered as part of the environment.

Origins

In terms of population dynamics, the concept of carrying capacity was not explicitly used in 1838 by the Belgian mathematician Pierre François Verhulst when he first published his equations based on research on modelling population growth,[3] but was popularised in the 1920 by the American biostatisticians Raymond Pearl and Lowell Reed.

The origins of the English term "carrying capacity" are uncertain, with researchers variously stating that it was used "in the context of international shipping"[4] or that it was first used during 19th-century laboratory experiments with micro-organisms.[5] A recent review finds the first use of the term in an 1845 report by the US Secretary of State to the US Senate.[4]

Factors

In the standard ecological algebra as illustrated in the simplified Verhulst model of population dynamics, carrying capacity is represented by the constant K:

${\displaystyle {\frac {dN}{dt}}=rN\left(1-{\frac {N}{K}}\right)}$

where N is the population, r is the maximum growth rate, K is the carrying capacity of the local environment, and dN/dt, the derivative of N with respect to time t, is the rate of change in population with time. Thus, the equation relates the growth rate of the population N to the current population size, incorporating the effect of the two constant parameters r and K. (Note that decrease is negative growth.) The choice of the letter K came from the German Kapazitätsgrenze (capacity limit).

This equation is a modification of the original Verhulst model:

${\displaystyle {\frac {dN}{dt}}=rN-\alpha N^{2}}$[3]

In this equation, the carrying capacity K, ${\displaystyle N^{*}}$, is

${\displaystyle N^{*}={\frac {r}{\alpha }}.}$

This is a graph of the population due to the logistic curve model. When the population is above the carrying capacity it decreases, and when it is below the carrying capacity it increases.

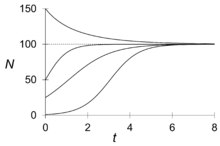
When the Verhulst model is plotted into a graph, the population change over time takes the form of a sigmoid curve, reaching its highest level at K. This is the logistic growth curve, and it is calculated with:

${\displaystyle f(x)={\frac {L}{1+e^{-k(x-x_{0})}}},}$

where

${\displaystyle e}$ = the natural logarithm base (also known as Euler's number),

${\displaystyle x_{0}}$ = the ${\displaystyle x}$ value of the sigmoid's midpoint,

${\displaystyle L}$ = the curve's maximum value,

${\displaystyle k}$ = the logistic growth rate or steepness of the curve.[6]

The logistic growth curve depicts how population growth rate and the carrying capacity are inter-connected. As illustrated in the logistic growth curve model, when the population size is small, the population increases exponentially. However, as population size nears the carrying capacity, the growth decreases and reaches zero at K.[7]

What determines a specific system's carrying capacity involves a limiting factor which may be something such as available supplies of food, water, nesting areas, space or amount of waste that can be absorbed. Where resources are finite, such as for a population of Osedax on a whale fall or bacteria in a petridish, the population will curve back down to zero after the resources have been exhausted, with the curve reaching its apogee at K. In systems in which resources are constantly replenished, the population will reach its equilibrium at K.

Software is available to help calculate the carrying capacity of a given natural environment.[8]

Humans

Main article: Human overpopulation

Several estimates of the carrying capacity of the earth for humans have been made with a wide range of population numbers. A 2001 UN report said that two-thirds of the estimates fall in the range of 4 billion to 16 billion with unspecified standard errors, with a median of about 10 billion.[9] Some of these issues have been studied by computer simulation models such as World3.

The application of the concept of carrying capacity for the human population, which exists in a non-equilibrium, has been criticized for not successfully being able to model the processes between humans and the environment.[10]

See also

• Tourism carrying capacity
• Inflection point
• Optimum population
• Overpopulation in wild animals
• Overshoot (ecology)
• Population ecology
• Population growth
• r/K selection theory
• Toxic capacity

References

1. Hui, C (2006). "Carrying capacity, population equilibrium, and environment's maximal load". Ecological Modelling. 192 (1–2): 317–320. doi:10.1016/j.ecolmodel.2005.07.001.
2. "Carrying Capacity". The Sustainable Scale Project. Retrieved 16 February 2017.
3. Verhulst, Pierre-François (1838). "Notice sur la loi que la population poursuit dans son accroissement" (PDF). Correspondance Mathématique et Physique. 10: 113–121. Retrieved 3 December 2014.
4. Sayre, N. F. (2008). "The Genesis, History, and Limits of Carrying Capacity". Annals of the Association of American Geographers. 98: 120–134. doi:10.1080/00045600701734356.
5. Zimmerer, Karl S. (1994). "Human Geography and the "New Ecology": The Prospect and Promise of Integration" (PDF). Annals of the Association of American Geographers. 84: 108–125. doi:10.1111/j.1467-8306.1994.tb01731.x.
6. Verhulst, Pierre-François (1845). "Recherches mathématiques sur la loi d'accroissement de la population" [Mathematical Researches into the Law of Population Growth Increase]. Nouveaux Mémoires de l'Académie Royale des Sciences et Belles-Lettres de Bruxelles. 18: 1–42. Retrieved 2013-02-18.
7. Swafford, Angela Lynn. "Logistic Population Growth: Equation, Definition & Graph." Study.com. N.p., 30 May 2015. Web. 21 May 2016. "Logistic Population Growth - Boundless Open Textbook." Boundless. N.p., n.d. Web. 21 May 2016.
8. Martire, Salvatore; Castellani, Valentina; Sala, Serenella (2015). "Carrying capacity assessment of forest resources: Enhancing environmental sustainability in energy production at local scale". Resources, Conservation and Recycling. 94: 11–20. doi:10.1016/j.resconrec.2014.11.002.
9. "UN World Population Report 2001" (PDF). p. 31. Retrieved 16 December 2008.
10. Cliggett, Lisa (2001). "Carrying Capacity's New Guise: Folk Models for Public Debate and Longitudinal Study of Environmental Change". Africa Today. 48: 3–19. doi:10.1353/at.2001.0003.

Further reading

• "Human Carrying Capacity is Determined by Food Availability" (PDF). Russel Hopfenberg, Psychiatry and Behavioral Sciences Department, Duke University, USA.