Hexagonal trapezohedron
The hexagonal trapezohedron or deltohedron is the fourth in an infinite series of face-uniform polyhedra which are dual polyhedron to the antiprisms. It has twelve faces which are congruent kites.
| Hexagonal trapezohedron | |
|---|---|
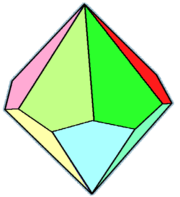 | |
| Type | trapezohedra |
| Conway | dA6 |
| Coxeter diagram | |
| Faces | 12 kites |
| Edges | 24 |
| Vertices | 14 |
| Face configuration | V6.3.3.3 |
| Symmetry group | D6d, [2+,12], (2*6), order 24 |
| Rotation group | D6, [2,6]+, (66), order 12 |
| Dual polyhedron | hexagonal antiprism |
| Properties | convex, face-transitive |
Variations
One degree of freedom within D6 symmetry changes the kites into congruent quadrilaterals with 3 edges lengths. In the limit, one edge of each quadrilateral goes to zero length, and these become bipyramids.
Crystal arrangements of atoms can repeat in space with hexagonal trapezohedral cells.[1]
If the kites surrounding the two peaks are of different shapes, it can only have C6v symmetry, order 12. These can be called unequal trapezohedra. The dual is an unequal antiprism, with the top and bottom polygons of different radii. If it twisted and unequal its symmetry is reduced to cyclic symmetry, C6 symmetry, order 6.
| Type | Twisted trapezohedra (isohedral) | Unequal trapezohedra | Unequal and twisted | |
|---|---|---|---|---|
| Symmetry | D6, (662), [6,2]+, order 12 | C6v, (*66), [6], order 12 | C6, (66), [6]+, order 6 | |
| Image (n=6) |
 |
 |
 |
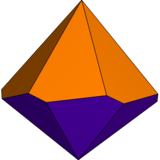 |
| Net |  |
 |
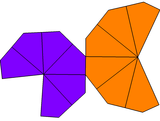 |
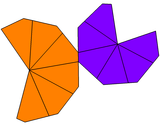 |
Related polyhedra
| Uniform hexagonal dihedral spherical polyhedra | ||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Symmetry: [6,2], (*622) | [6,2]+, (622) | [6,2+], (2*3) | ||||||||||||
 |
 |
 |
 |
 |
 |
 | ||||||||
| {6,2} | t{6,2} | r{6,2} | t{2,6} | {2,6} | rr{6,2} | tr{6,2} | sr{6,2} | s{2,6} | ||||||
| Duals to uniforms | ||||||||||||||
 |
 |
 |
 |
 |
 |
 |
 |
 | ||||||
| V62 | V122 | V62 | V4.4.6 | V26 | V4.4.6 | V4.4.12 | V3.3.3.6 | V3.3.3.3 | ||||||
| Family of trapezohedra Vn.3.3.3 | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Polyhedron |  |
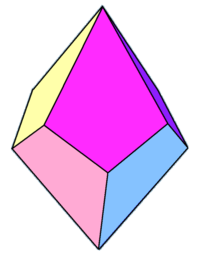 |
 |
 |
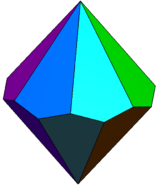 |
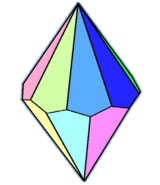 |
 |
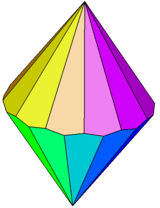 |
|||
| Tiling |  |
 |
 |
 |
 |
 |
 |
 |
|||
| Config. | V2.3.3.3 | V3.3.3.3 | V4.3.3.3 | V5.3.3.3 | V6.3.3.3 | V7.3.3.3 | V8.3.3.3 | V10.3.3.3 | V12.3.3.3 | ... | V∞.3.3.3 |
External links
- Weisstein, Eric W. "Trapezohedron". MathWorld.
- Virtual Reality Polyhedra The Encyclopedia of Polyhedra