Square pyramid
In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it is a right square pyramid, and has C4v symmetry. If all edges are equal, it is an equilateral square pyramid,[1] the Johnson solid J1.
| Square pyramid | |
|---|---|
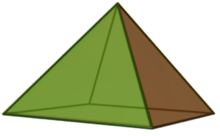 | |
| Type | Johnson J92 – J1 – J2 |
| Faces | 4 triangles 1 square |
| Edges | 8 |
| Vertices | Trryru Ru], (*44) |
| Vertex configuration | 4(32.4) (34) |
| Rotation group | C4, [4]+, (44) |
| Dual polyhedron | self |
| Properties | convex |
| Net | |
 | |
General square pyramid
A possibly oblique square pyramid with base length l and perpendicular height h has volume:
- .
Right square pyramid
In a right square pyramid, all the lateral edges have the same length, and the sides other than the base are congruent isosceles triangles.
A right square pyramid with base length l and height h has surface area and volume:
- .
The lateral edge length is:
- ,
and the slant height is:
- .
The dihedral angles are:
- between the base and a side: ;
- between two sides: .
Equilateral square pyramid, Johnson solid J1
If all the edges have the same length, then the sides are equilateral triangles, and the pyramid is an equilateral square pyramid, Johnson solid J1.
The Johnson square pyramid can be characterized by a single edge-length parameter l. The height h (from the midpoint of the square to the apex), the surface area A (including all five faces), and the volume V of such a pyramid are:
Graph
A square pyramid can be represented by the Wheel graph W5.
Related polyhedra and honeycombs
| Regular pyramids | ||||||||
|---|---|---|---|---|---|---|---|---|
| Digonal | Triangular | Square | Pentagonal | Hexagonal | Heptagonal | Octagonal | Enneagonal | Decagonal... |
| Improper | Regular | Equilateral | Isosceles | |||||
 |
 |
 |
 | |||||
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
|---|---|---|
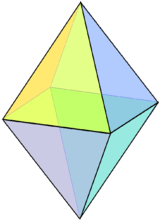
| A regular octahedron can be considered a square bipyramid, i.e. two Johnson square pyramids connected base-to-base. | The tetrakis hexahedron can be constructed from a cube with short square pyramids added to each face. | Square frustum is a square pyramid with the apex truncated. |
Square pyramids fill space with tetrahedra, truncated cubes or cuboctahedra.[2]
Dual polyhedron
The square pyramid is topologically a self-dual polyhedron. The dual edge lengths are different due to the polar reciprocation.
| Dual Square pyramid | Net of dual |
|---|---|
 |
 |
References
- Franz Hocevar, Solid Geometry, 1903, p. 44
- http://woodenpolyhedra.web.fc2.com/JohnsonHoneycomb.pdf
External links
- Eric W. Weisstein, Square pyramid (Johnson solid) at MathWorld.
- Weisstein, Eric W. "Wheel graph". MathWorld.
- Square Pyramid -- Interactive Polyhedron Model
- Virtual Reality Polyhedra www.georgehart.com: The Encyclopedia of Polyhedra (VRML model)