Order-6 apeirogonal tiling
In geometry, the order-6 apeirogonal tiling is a regular tiling of the hyperbolic plane. It has Schläfli symbol of {∞,6}.
| Order-6 apeirogonal tiling | |
|---|---|
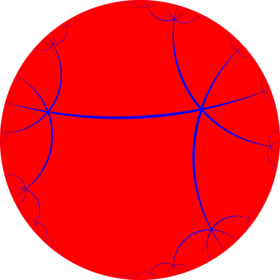 Poincaré disk model of the hyperbolic plane | |
| Type | Hyperbolic regular tiling |
| Vertex configuration | ∞6 |
| Schläfli symbol | {∞,6} |
| Wythoff symbol | 6 | ∞ 2 |
| Coxeter diagram |     |
| Symmetry group | [∞,6], (*∞62) |
| Dual | Infinite-order hexagonal tiling |
| Properties | Vertex-transitive, edge-transitive, face-transitive edge-transitive |
Symmetry
The dual to this tiling represents the fundamental domains of [∞,6*] symmetry, orbifold notation *∞∞∞∞∞∞ symmetry, a hexagonal domain with five ideal vertices.
The order-6 apeirogonal tiling can be uniformly colored with 6 colored apeirogons around each vertex, and coxeter diagram: 
Related polyhedra and tiling
This tiling is also topologically related as a part of sequence of regular polyhedra and tilings with four faces per vertex, starting with the octahedron, with Schläfli symbol {n,6}, and Coxeter diagram 
| Regular tilings {n,6} | ||||||||
|---|---|---|---|---|---|---|---|---|
| Spherical | Euclidean | Hyperbolic tilings | ||||||
 {2,6}  |
 {3,6}  |
 {4,6}  |
 {5,6}  |
 {6,6} |
 {7,6}  |
 {8,6}  |
... | {∞,6} |
gollark: It was only picked up because they foolishly used a deprecated function to do this.
gollark: https://schneider.dev/blog/event-stream-vulnerability-explained/
gollark: Every person you depend on *can inject code in your application* and it would be pretty hard to notice. We have literally *seen* this attack.
gollark: Specifically, slower package management (especially with transistive dependencies), worse performance from loading more files for no good reason, and, more importantly, *security*.
gollark: Anyway, adding more packages for basically-one-line tasks incurs costs.
See also
 |
Wikimedia Commons has media related to Order-6 apeirogonal tiling. |
- Tilings of regular polygons
- List of uniform planar tilings
- List of regular polytopes
References
- John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 19, The Hyperbolic Archimedean Tessellations)
- "Chapter 10: Regular honeycombs in hyperbolic space". The Beauty of Geometry: Twelve Essays. Dover Publications. 1999. ISBN 0-486-40919-8. LCCN 99035678.
External links
- Weisstein, Eric W. "Hyperbolic tiling". MathWorld.
- Weisstein, Eric W. "Poincaré hyperbolic disk". MathWorld.
- Hyperbolic and Spherical Tiling Gallery
- KaleidoTile 3: Educational software to create spherical, planar and hyperbolic tilings
- Hyperbolic Planar Tessellations, Don Hatch
  | ||||||
| ||||||
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.