Norbert Wiener

Norbert Wiener (November 26, 1894 – March 18, 1964) was an American mathematician and philosopher. He was a professor of mathematics at the Massachusetts Institute of Technology (MIT). A child prodigy, Wiener later became an early researcher in stochastic and mathematical noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems.

Norbert Wiener
Born(1894-11-26)November 26, 1894
Columbia, Missouri, U.S.
DiedMarch 18, 1964(1964-03-18) (aged 69)
Stockholm, Sweden
NationalityAmerican
EducationTufts College, B.A. 1909
Cornell University, M.A., 1911
Harvard University, Ph.D. 1913
Known for
AwardsBôcher Memorial Prize (1933)
National Medal of Science (1963)
Scientific career
FieldsMathematics
Cybernetics
InstitutionsMassachusetts Institute of Technology
ThesisA Comparison Between the Treatment of the Algebra of Relatives by Schroeder and that by Whitehead and Russell (1913)
Doctoral advisors
  • Karl Schmidt[1]
Other academic advisorsJosiah Royce[2]
Doctoral students

Wiener is considered the originator of cybernetics, a formalization of the notion of feedback, with implications for engineering, systems control, computer science, biology, neuroscience, philosophy, and the organization of society.

Norbert Wiener is credited as being one of the first to theorize that all intelligent behavior was the result of feedback mechanisms, that could possibly be simulated by machines and was an important early step towards the development of modern artificial intelligence.[3]

Biography

Youth

Wiener was born in Columbia, Missouri, the first child of Leo Wiener and Bertha Kahn, Jews[4] from Poland and Germany, respectively. Through his father, he was related to Maimonides, the famous rabbi, philosopher and physician from Al Andalus, as well as to Akiva Eger, chief rabbi of Posen from 1815 to 1837.[5] Leo had educated Norbert at home until 1903, employing teaching methods of his own invention, except for a brief interlude when Norbert was 7 years of age. Earning his living teaching German and Slavic languages, Leo read widely and accumulated a personal library from which the young Norbert benefited greatly. Leo also had ample ability in mathematics and tutored his son in the subject until he left home. In his autobiography, Norbert described his father as calm and patient, unless he (Norbert) failed to give a correct answer, at which his father would lose his temper.

A child prodigy, he graduated from Ayer High School in 1906 at 11 years of age, and Wiener then entered Tufts College. He was awarded a BA in mathematics in 1909 at the age of 14, whereupon he began graduate studies of zoology at Harvard. In 1910 he transferred to Cornell to study philosophy. He graduated in 1911 at 17 years of age.

Harvard and World War I

The next year he returned to Harvard, while still continuing his philosophical studies. Back at Harvard, Wiener became influenced by Edward Vermilye Huntington, whose mathematical interests ranged from axiomatic foundations to engineering problems. Harvard awarded Wiener a Ph.D. in June 1913, when he was only 19 years old, for a dissertation on mathematical logic (a comparison of the work of Ernst Schröder with that of Alfred North Whitehead and Bertrand Russell), supervised by Karl Schmidt, the essential results of which were published as Wiener (1914). He was one of the youngest to achieve such a feat. In that dissertation, he was the first to state publicly that ordered pairs can be defined in terms of elementary set theory. Hence relations can be defined by set theory, thus the theory of relations does not require any axioms or primitive notions distinct from those of set theory. In 1921, Kazimierz Kuratowski proposed a simplification of Wiener's definition of ordered pairs, and that simplification has been in common use ever since. It is (x, y) = {{x}, {x, y}}.

In 1914, Wiener traveled to Europe, to be taught by Bertrand Russell and G. H. Hardy at Cambridge University, and by David Hilbert and Edmund Landau at the University of Göttingen. At Göttingen he also attended three courses with Edmund Husserl "one on Kant's ethical writings, one on the principles of Ethics, and the seminary on Phenomenology." (Letter to Russell, c. June or July, 1914). During 1915–16, he taught philosophy at Harvard, then was an engineer for General Electric and wrote for the Encyclopedia Americana. Wiener was briefly a journalist for the Boston Herald, where he wrote a feature story on the poor labor conditions for mill workers in Lawrence, Massachusetts, but he was fired soon afterwards for his reluctance to write favorable articles about a politician the newspaper's owners sought to promote.[6]

Although Wiener eventually became a staunch pacifist, he eagerly contributed to the war effort in World War I. In 1916, with America's entry into the war drawing closer, Wiener attended a training camp for potential military officers, but failed to earn a commission. One year later Wiener again tried to join the military, but the government again rejected him due to his poor eyesight. In the summer of 1918, Oswald Veblen invited Wiener to work on ballistics at the Aberdeen Proving Ground in Maryland.[7] Living and working with other mathematicians strengthened his interest in mathematics. However, Wiener was still eager to serve in uniform, and decided to make one more attempt to enlist, this time as a common soldier. Wiener wrote in a letter to his parents, "I should consider myself a pretty cheap kind of a swine if I were willing to be an officer but unwilling to be a soldier."[8] This time the army accepted Wiener into its ranks and assigned him, by coincidence, to a unit stationed at Aberdeen, Maryland. World War I ended just days after Wiener's return to Aberdeen and Wiener was discharged from the military in February 1919.[9]

After the war
Norbert Wiener was regarded as a semi-legendary figure at MIT
Norbert (standing) and Margaret (sitting) Wiener at the International Congress of Mathematicians, Zurich 1932

Wiener was unable to secure a permanent position at Harvard, a situation he blamed largely on anti-semitism at the university and in particular on the antipathy of Harvard mathematician G. D. Birkhoff.[10] He was also rejected for a position at the University of Melbourne. At W. F. Osgood's suggestion, Wiener became an instructor of mathematics at MIT, where he spent the remainder of his career, becoming promoted eventually to professor. For many years, a photograph of him was prominently displayed in the Infinite Corridor, often used in giving directions, but as of 2017, it has been removed.[11]

In 1926, Wiener returned to Europe as a Guggenheim scholar. He spent most of his time at Göttingen and with Hardy at Cambridge, working on Brownian motion, the Fourier integral, Dirichlet's problem, harmonic analysis, and the Tauberian theorems.

In 1926, Wiener's parents arranged his marriage to a German immigrant, Margaret Engemann; they had two daughters. His sister, Constance, married Philip Franklin. Their daughter, Janet, Wiener's niece, married Václav E. Beneš.[12]

Many tales, perhaps apocryphal, were told of him at MIT, especially concerning his absent-mindedness. It was said that he returned home once to find his house empty. He inquired of a neighborhood girl the reason, and she said that the family had moved elsewhere that day. He thanked her for the information and she replied, "That's why I stayed behind, Daddy!"[13]

In the run-up to World War II (1939–45) Wiener became a member of the China Aid Society and the Emergency Committee in Aid of Displaced German Scholars.[14] He was interested in placing scholars such as Yuk-Wing Lee and Antoni Zygmund who had lost their positions.[15]

During and after World War II

During World War II, his work on the automatic aiming and firing of anti-aircraft guns caused Wiener to investigate information theory independently of Claude Shannon and to invent the Wiener filter. (To him is due the now standard practice of modeling an information source as a random process—in other words, as a variety of noise.) His anti-aircraft work eventually led him to formulate cybernetics.[16] After the war, his fame helped MIT to recruit a research team in cognitive science, composed of researchers in neuropsychology and the mathematics and biophysics of the nervous system, including Warren Sturgis McCulloch and Walter Pitts. These men later made pioneering contributions to computer science and artificial intelligence. Soon after the group was formed, Wiener suddenly ended all contact with its members, mystifying his colleagues. This emotionally traumatized Pitts, and led to his career decline. In their biography of Wiener, Conway and Siegelman suggest that Wiener's wife Margaret, who detested McCulloch's bohemian lifestyle, engineered the breach.[17]

Wiener later helped develop the theories of cybernetics, robotics, computer control, and automation. He discussed the modeling of neurons with John von Neumann, and in a letter from November 1946 von Neumann presented his thoughts in advance of a meeting with Wiener.[18]

Wiener always shared his theories and findings with other researchers, and credited the contributions of others. These included Soviet researchers and their findings. Wiener's acquaintance with them caused him to be regarded with suspicion during the Cold War. He was a strong advocate of automation to improve the standard of living, and to end economic underdevelopment. His ideas became influential in India, whose government he advised during the 1950s.

After the war, Wiener became increasingly concerned with what he believed was political interference with scientific research, and the militarization of science. His article "A Scientist Rebels" from the January 1947 issue of The Atlantic Monthly[19] urged scientists to consider the ethical implications of their work. After the war, he refused to accept any government funding or to work on military projects. The way Wiener's beliefs concerning nuclear weapons and the Cold War contrasted with those of von Neumann is the major theme of the book John Von Neumann and Norbert Wiener.[20]

Wiener was a participant of the Macy conferences. He died in March 1964, aged 69, in Stockholm, from a heart attack. Wiener and his wife are buried at the Vittum Hill Cemetery in Sandwich, New Hampshire.

Awards and honors

Doctoral students

Work

Information is information, not matter or energy.

— Norbert Wiener, Cybernetics: Or Control and Communication in the Animal and the Machine

Wiener was an early studier of stochastic and mathematical noise processes, contributing work relevant to electronic engineering, electronic communication, and control systems. It was Wiener's idea to model a signal as if it were an exotic type of noise, giving it a sound mathematical basis. The example often given to students is that English text could be modeled as a random string of letters and spaces, where each letter of the alphabet (and the space) has an assigned probability. But Wiener dealt with analog signals, where such a simple example doesn't exist. Wiener's early work on information theory and signal processing was limited to analog signals, and was largely forgotten with the development of the digital theory.[24]

Wiener is one of the key originators of cybernetics, a formalization of the notion of feedback, with many implications for engineering, systems control, computer science, biology, philosophy, and the organization of society.

Wiener's work with cybernetics influenced Gregory Bateson and Margaret Mead, and through them, anthropology, sociology, and education.[25]

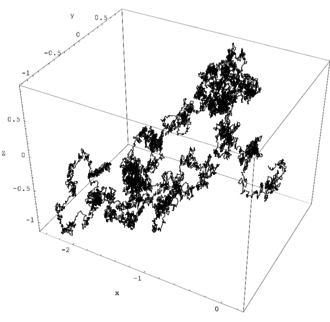
In the mathematical field of probability, the "Wiener sausage" is a neighborhood of the trace of a Brownian motion up to a time t, given by taking all points within a fixed distance of Brownian motion. It can be visualized as a cylinder of fixed radius the centerline of which is Brownian motion.

Wiener equation

A simple mathematical representation of Brownian motion, the Wiener equation, named after Wiener, assumes the current velocity of a fluid particle fluctuates randomly.

Wiener filter

For signal processing, the Wiener filter is a filter proposed by Wiener during the 1940s and published in 1942 as a classified document. Its purpose is to reduce the amount of noise present in a signal by comparison with an estimate of the desired noiseless signal. Wiener developed the filter at the Radiation Laboratory at MIT to predict the position of German bombers from radar reflections. It is necessary to predict the future, because by the time the shell reaches the vicinity of the target, the target has moved, and may have changed direction slightly. They even modeled the muscle response of the pilot, which led eventually to cybernetics. The unmanned V1's were particularly easy to model, and on a good day, American guns fitted with Wiener filters would shoot down 99 out of 100 V1's as they entered Britain from the English channel, on their way to London. What emerged was a mathematical theory of great generality—a theory for predicting the future as best one can on the basis of incomplete information about the past. It was a statistical theory that included applications that did not, strictly speaking, predict the future, but only tried to remove noise. It made use of Wiener's earlier work on integral equations and Fourier transforms.[26] [27]

In mathematics

Wiener took a great interest in the mathematical theory of Brownian motion (named after Robert Brown) proving many results now widely known such as the non-differentiability of the paths. Consequently, the one-dimensional version of Brownian motion was named the Wiener process. It is the best known of the Lévy processes, càdlàg stochastic processes with stationary statistically independent increments, and occurs frequently in pure and applied mathematics, physics and economics (e.g. on the stock-market).

Wiener's Tauberian theorem, a 1932 result of Wiener, developed Tauberian theorems in summability theory, on the face of it a chapter of real analysis, by showing that most of the known results could be encapsulated in a principle taken from harmonic analysis. In its present formulation, the theorem of Wiener does not have any obvious association with Tauberian theorems, which deal with infinite series; the translation from results formulated for integrals, or using the language of functional analysis and Banach algebras, is however a relatively routine process.

The Paley–Wiener theorem relates growth properties of entire functions on Cn and Fourier transformation of Schwartz distributions of compact support.

The Wiener–Khinchin theorem, (also known as the Wiener – Khintchine theorem and the Khinchin – Kolmogorov theorem), states that the power spectral density of a wide-sense-stationary random process is the Fourier transform of the corresponding autocorrelation function.

An abstract Wiener space is a mathematical object in measure theory, used to construct a "decent", strictly positive and locally finite measure on an infinite-dimensional vector space. Wiener's original construction only applied to the space of real-valued continuous paths on the unit interval, known as classical Wiener space. Leonard Gross provided the generalization to the case of a general separable Banach space.

The notion of a Banach space itself was discovered independently by both Wiener and Stefan Banach at around the same time.[28]

The Norbert Wiener Center for Harmonic Analysis and Applications (NWC) in the Department of Mathematics at the University of Maryland, College Park is devoted to the scientific and mathematical legacy of Norbert Wiener. The NWC website highlights the research activities of the Center. Further, each year the Norbert Wiener Center hosts the February Fourier Talks, a two-day national conference displaying advances in pure and applied harmonic analysis in industry, government, and academia.

His work with Mary Brazier is referenced in Avis DeVoto's As Always, Julia.[29]

A character named after him appears briefly in the Hugo Award winner The Three Body Problem by Liu Cixin.[30]

A flagship named after him appears briefly in Citizen of the Galaxy by Robert Heinlein.[31]

The song Dedicated to Norbert Wiener appears as the second track on the 1980 album Why? by G.G. Tonet (Luigi Tonet), released on the Italian It Why label.[32]

Publications

Wiener wrote many books and hundreds of articles:[33]

  • 1914, "A simplification in the logic of relations". Proc. Camb. Phil. Soc. 13: 387–390. 1912–14. Reprinted in van Heijenoort, Jean (1967). From Frege to Gödel: A Source Book in Mathematical Logic, 1879–1931. Harvard University Press. pp. 224–7.
  • 1930, Wiener, Norbert (1930). "Generalized harmonic analysis". Acta Math. 55 (1): 117–258. doi:10.1007/BF02546511.
  • 1933, The Fourier Integral and Certain of its Applications Cambridge Univ. Press; reprint by Dover, CUP Archive 1988 ISBN 0-521-35884-1
  • 1942, Extrapolation, Interpolation and Smoothing of Stationary Time Series. A war-time classified report nicknamed "the yellow peril" because of the color of the cover and the difficulty of the subject. Published postwar 1949 MIT Press. http://www.isss.org/lumwiener.htm])
  • 1948, Cybernetics: Or Control and Communication in the Animal and the Machine. Paris, (Hermann & Cie) & Camb. Mass. (MIT Press) ISBN 978-0-262-73009-9; 2nd revised ed. 1961.
  • 1950, The Human Use of Human Beings. The Riverside Press (Houghton Mifflin Co.).
  • 1958, Nonlinear Problems in Random Theory. MIT Press & Wiley.
  • 1964, Selected Papers of Norbert Wiener. Cambridge Mass. 1964 (MIT Press & SIAM)
  • 1964, God & Golem, Inc.: A Comment on Certain Points Where Cybernetics Impinges on Religion. MIT Press.
  • 1966, Levinson, N. (1966). "Norbert Wiener 1894–1964". Bull. Amer. Math. Soc. 72 (1 Part 2): 1–33. doi:10.1090/S0002-9904-1966-11450-7. Published in book form.
  • 1966, Generalized Harmonic Analysis and Tauberian Theorems. MIT Press.
  • 1993, Invention: The Care and Feeding of Ideas. MIT Press. 1993. ISBN 978-0-262-73111-9. This was written in 1954 but Wiener abandoned the project at the editing stage and returned his advance. MIT Press published it posthumously in 1993.
  • 1976–84, The Mathematical Work of Norbert Wiener. Masani P (ed) 4 vols, Camb. Mass. (MIT Press). This contains a complete collection of Wiener's mathematical papers with commentaries.

Fiction:

  • 1959,The Tempter. Random House.

Autobiography:

  • 1953. Ex-Prodigy: My Childhood and Youth. MIT Press.
  • 1956. I am a Mathematician. London (Gollancz).

Under the name "W. Norbert":

gollark: Code is here if anyone wants to continue, but I'm doing a more traditional thing since time travel isn't working out.
gollark: I solved that issue and ran into other incomprehensible issues.
gollark: Also, we write programs for it.
gollark: Ah, but it has unknown iteration count.
gollark: Have you tried the ITERATED PRISONER'S DILEMMA competition?

See also

Notes
  1. Norbert Wiener at the Mathematics Genealogy Project
  2. Leone Montagnini, Harmonies of Disorder – Norbert Wiener: A Mathematician-Philosopher of Our Time, Springer, 2017, p. 61.
  3. Research, AI (11 January 2019). "The Beginnings of AI Research". world-information.org. Archived from the original on 11 January 2019. Retrieved 11 January 2019.
  4. "Norbert Wiener". NNDB. Archived from the original on April 2, 2014. Retrieved March 25, 2014.
  5. Leone Montagnini, Harmonies of Disorder: Norbert Wiener: A Mathematician-Philosopher of Our Time, Springer (2017), p. 4
  6. Conway & Siegelman 2005, p. 45
  7. Conway & Siegelman 2005, pp. 41–43
  8. Conway & Siegelman 2005, p. 43
  9. Conway & Siegelman 2005, pp. 43–44
  10. Conway & Siegelman 2005, pp. 40, 45
  11. "Does the infinite corridor still have a poster of Norbert Wiener and cybernetics?". Retrieved 2019-10-27.
  12. Franklin biography Archived 2018-07-13 at the Wayback Machine. History.mcs.st-and.ac.uk. Retrieved on 2013-11-02.
  13. Adams, Hass & Thompson 1998, p. 8
  14. Masani, Pesi R. (2012-12-06), Norbert Wiener 1894–1964, Birkhäuser, p. 167, ISBN 978-3-0348-9252-0, archived from the original on 2017-02-22, retrieved 2016-03-20
  15. McCavitt, Mary Jane (September 2, 2009), Guide to the Papers of Norbert Wiener (PDF), Massachusetts Institute of Technology Libraries, p. 15, archived from the original (PDF) on November 12, 2015, retrieved 2016-03-20
  16. Conway & Siegelman 2005, p. 12
  17. Conway & Siegelman 2005, pp. 223–7
  18. Letters to Norbert Wiener in John von Neumann: Selected Letters, edited by Miklós Rédei, in History of Mathematics, Volume 27, jointly published by the American Mathematical Society and the London Mathematical Society, 2005
  19. Wiener, Norbert (January 1947). "A Scientist Rebels". Atlantic Monthly. p. 46. Archived from the original on 2018-10-26. Retrieved 2018-10-26.
  20. Heims 1980
  21. "National Book Awards – 1965" Archived 2019-01-31 at the Wayback Machine. National Book Foundation. Retrieved 2012-03-05.
  22. "Norbert Wiener Center for Harmonic Analysis and Applications". University of Maryland, College Park. Archived from the original on 2018-04-04. Retrieved 2009-09-24.
  23. Mandrekar, V.; Masani, P. R., eds. (1997). Proceedings of Symposia in Applied Mathematics Vol 52: Proceedings of the Norbert Wiener Centenary Congress 1994. Providence, Rhode Island: Michigan State University. p. 541. ISBN 978-0-8218-0452-0.
  24. John Von Neumann and Norbert Wiener: From Mathematics to the Technologies of Life and Death, Steve Joshua Heims, MIT Press, 1980
  25. Heims, Steve P. (April 1977). "Gregory Bateson and the mathematicians: From interdisciplinary interaction to societal functions". Journal of the History of the Behavioral Sciences. 13 (2): 141–159. doi:10.1002/1520-6696(197704)13:2<141::AID-JHBS2300130205>3.0.CO;2-G. PMID 325068.
  26. John Von Neumann and Norbert Wiener: From Mathematics to the Technologies of Life and Death, Steve Joshua Heims, MIT Press, 1980, p.183
  27. Norbert Wiener, Extrapolation, Interpolation and Smoothing of Stationary Time Series, MIT Press, 1949. Originally published as a classified document in 1942
  28. Wiener, Norbert (1923). "Note on a paper of M. Banach". Fund. Math. 4: 136–143. doi:10.4064/fm-4-1-136-143. See Albiac, F.; Kalton, N. (2006). Topics in Banach Space Theory. Graduate Texts in Mathematics. 233. New York: Springer. p. 15. ISBN 978-0-387-28141-4.
  29. Reardon, Joan. As Always, Julia. Houghton Mifflin, 2010. 223.
  30. Liu, Cixin (2015). The Three Body Problem. Chongqing Publishing Group. ISBN 9787229100605.
  31. Heinlein, Robert (1957). "14". Citizen of the Galaxy. Charles Scribner's Sons.
  32. "G.G. Tonet – Why?". Discogs. Archived from the original on 25 February 2020. Retrieved 2 May 2019.
  33. A full bibliography is given by the Cybernetics Society Publications of Norbert Wiener Archived 2007-02-05 at the Wayback Machine

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.