Light
Light or visible light is electromagnetic radiation within the portion of the electromagnetic spectrum that can be perceived by the human eye.[1] Visible light is usually defined as having wavelengths in the range of 400–700 nanometers (nm), or 4.00 × 10−7 to 7.00 × 10−7 m, between the infrared (with longer wavelengths) and the ultraviolet (with shorter wavelengths).[2][3] This wavelength means a frequency range of roughly 430–750 terahertz (THz).
The main source of light on Earth is the Sun. Sunlight provides the energy that green plants use to create sugars mostly in the form of starches, which release energy into the living things that digest them. This process of photosynthesis provides virtually all the energy used by living things. Historically, another important source of light for humans has been fire, from ancient campfires to modern kerosene lamps. With the development of electric lights and power systems, electric lighting has effectively replaced firelight. Some species of animals generate their own light, a process called bioluminescence. For example, fireflies use light to locate mates, and vampire squids use it to hide themselves from prey.
The primary properties of visible light are intensity, propagation direction, frequency or wavelength spectrum, and polarization, while its speed in a vacuum, 299,792,458 meters per second, is one of the fundamental constants of nature. Visible light, as with all types of electromagnetic radiation (EMR), is experimentally found to always move at this speed in a vacuum.[4]
In physics, the term light sometimes refers to electromagnetic radiation of any wavelength, whether visible or not.[5][6] In this sense, gamma rays, X-rays, microwaves and radio waves are also light. Like all types of EM radiation, visible light propagates as waves. However, the energy imparted by the waves is absorbed at single locations the way particles are absorbed. The absorbed energy of the EM waves is called a photon, and represents the quanta of light. When a wave of light is transformed and absorbed as a photon, the energy of the wave instantly collapses to a single location, and this location is where the photon "arrives." This is what is called the wave function collapse. This dual wave-like and particle-like nature of light is known as the wave–particle duality. The study of light, known as optics, is an important research area in modern physics.
Electromagnetic spectrum and visible light

Generally, EM radiation (the designation "radiation" excludes static electric, magnetic, and near fields), or EMR, is classified by wavelength into radio waves, microwaves, infrared, the visible spectrum that we perceive as light, ultraviolet, X-rays, and gamma rays.
The behavior of EMR depends on its wavelength. Higher frequencies have shorter wavelengths, and lower frequencies have longer wavelengths. When EMR interacts with single atoms and molecules, its behavior depends on the amount of energy per quantum it carries.
EMR in the visible light region consists of quanta (called photons) that are at the lower end of the energies that are capable of causing electronic excitation within molecules, which leads to changes in the bonding or chemistry of the molecule. At the lower end of the visible light spectrum, EMR becomes invisible to humans (infrared) because its photons no longer have enough individual energy to cause a lasting molecular change (a change in conformation) in the visual molecule retinal in the human retina, which change triggers the sensation of vision.
There exist animals that are sensitive to various types of infrared, but not by means of quantum-absorption. Infrared sensing in snakes depends on a kind of natural thermal imaging, in which tiny packets of cellular water are raised in temperature by the infrared radiation. EMR in this range causes molecular vibration and heating effects, which is how these animals detect it.
Above the range of visible light, ultraviolet light becomes invisible to humans, mostly because it is absorbed by the cornea below 360 nm and the internal lens below 400 nm. Furthermore, the rods and cones located in the retina of the human eye cannot detect the very short (below 360 nm) ultraviolet wavelengths and are in fact damaged by ultraviolet. Many animals with eyes that do not require lenses (such as insects and shrimp) are able to detect ultraviolet, by quantum photon-absorption mechanisms, in much the same chemical way that humans detect visible light.
Various sources define visible light as narrowly as 420–680 nm[7][8] to as broadly as 380–800 nm.[9][10] Under ideal laboratory conditions, people can see infrared up to at least 1050 nm;[11] children and young adults may perceive ultraviolet wavelengths down to about 310–313 nm.[12][13][14]
Plant growth is also affected by the color spectrum of light, a process known as photomorphogenesis.
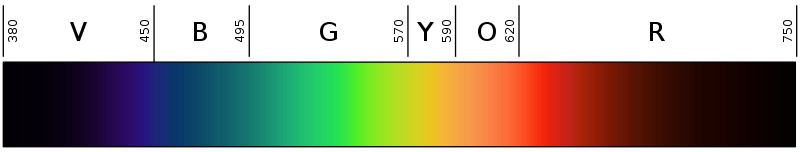
Speed of light
The speed of light in a vacuum is defined to be exactly 299,792,458 m/s (approx. 186,282 miles per second). The fixed value of the speed of light in SI units results from the fact that the meter is now defined in terms of the speed of light. All forms of electromagnetic radiation move at exactly this same speed in vacuum.
Different physicists have attempted to measure the speed of light throughout history. Galileo attempted to measure the speed of light in the seventeenth century. An early experiment to measure the speed of light was conducted by Ole Rømer, a Danish physicist, in 1676. Using a telescope, Rømer observed the motions of Jupiter and one of its moons, Io. Noting discrepancies in the apparent period of Io's orbit, he calculated that light takes about 22 minutes to traverse the diameter of Earth's orbit.[15] However, its size was not known at that time. If Rømer had known the diameter of the Earth's orbit, he would have calculated a speed of 227,000,000 m/s.
Another more accurate measurement of the speed of light was performed in Europe by Hippolyte Fizeau in 1849. Fizeau directed a beam of light at a mirror several kilometers away. A rotating cog wheel was placed in the path of the light beam as it traveled from the source, to the mirror and then returned to its origin. Fizeau found that at a certain rate of rotation, the beam would pass through one gap in the wheel on the way out and the next gap on the way back. Knowing the distance to the mirror, the number of teeth on the wheel, and the rate of rotation, Fizeau was able to calculate the speed of light as 313,000,000 m/s.
Léon Foucault carried out an experiment which used rotating mirrors to obtain a value of 298,000,000 m/s in 1862. Albert A. Michelson conducted experiments on the speed of light from 1877 until his death in 1931. He refined Foucault's methods in 1926 using improved rotating mirrors to measure the time it took light to make a round trip from Mount Wilson to Mount San Antonio in California. The precise measurements yielded a speed of 299,796,000 m/s.[16]
The effective velocity of light in various transparent substances containing ordinary matter, is less than in vacuum. For example, the speed of light in water is about 3/4 of that in vacuum.
Two independent teams of physicists were said to bring light to a "complete standstill" by passing it through a Bose–Einstein condensate of the element rubidium, one team at Harvard University and the Rowland Institute for Science in Cambridge, Massachusetts, and the other at the Harvard–Smithsonian Center for Astrophysics, also in Cambridge.[17] However, the popular description of light being "stopped" in these experiments refers only to light being stored in the excited states of atoms, then re-emitted at an arbitrary later time, as stimulated by a second laser pulse. During the time it had "stopped" it had ceased to be light.
Optics
The study of light and the interaction of light and matter is termed optics. The observation and study of optical phenomena such as rainbows and the aurora borealis offer many clues as to the nature of light.
Refraction


Refraction is the bending of light rays when passing through a surface between one transparent material and another. It is described by Snell's Law:
where θ1 is the angle between the ray and the surface normal in the first medium, θ2 is the angle between the ray and the surface normal in the second medium, and n1 and n2 are the indices of refraction, n = 1 in a vacuum and n > 1 in a transparent substance.
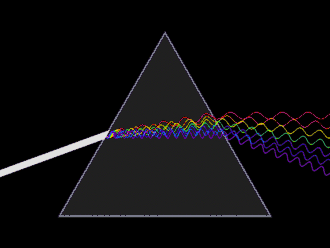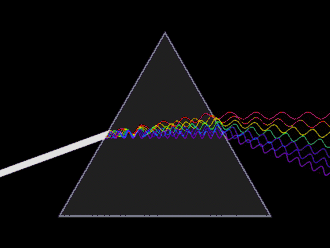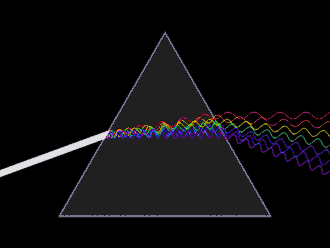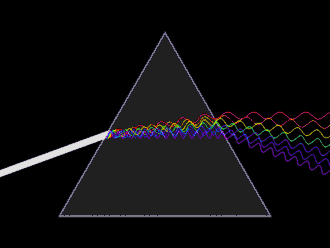
When a beam of light crosses the boundary between a vacuum and another medium, or between two different media, the wavelength of the light changes, but the frequency remains constant. If the beam of light is not orthogonal (or rather normal) to the boundary, the change in wavelength results in a change in the direction of the beam. This change of direction is known as refraction.
The refractive quality of lenses is frequently used to manipulate light in order to change the apparent size of images. Magnifying glasses, spectacles, contact lenses, microscopes and refracting telescopes are all examples of this manipulation.
Light sources
There are many sources of light. A body at a given temperature emits a characteristic spectrum of black-body radiation. A simple thermal source is sunlight, the radiation emitted by the chromosphere of the Sun at around 6,000 kelvins (5,730 degrees Celsius; 10,340 degrees Fahrenheit) peaks in the visible region of the electromagnetic spectrum when plotted in wavelength units[18] and roughly 44% of sunlight energy that reaches the ground is visible.[19] Another example is incandescent light bulbs, which emit only around 10% of their energy as visible light and the remainder as infrared. A common thermal light source in history is the glowing solid particles in flames, but these also emit most of their radiation in the infrared, and only a fraction in the visible spectrum.
The peak of the black-body spectrum is in the deep infrared, at about 10 micrometre wavelength, for relatively cool objects like human beings. As the temperature increases, the peak shifts to shorter wavelengths, producing first a red glow, then a white one, and finally a blue-white color as the peak moves out of the visible part of the spectrum and into the ultraviolet. These colors can be seen when metal is heated to "red hot" or "white hot". Blue-white thermal emission is not often seen, except in stars (the commonly seen pure-blue color in a gas flame or a welder's torch is in fact due to molecular emission, notably by CH radicals (emitting a wavelength band around 425 nm, and is not seen in stars or pure thermal radiation).
Atoms emit and absorb light at characteristic energies. This produces "emission lines" in the spectrum of each atom. Emission can be spontaneous, as in light-emitting diodes, gas discharge lamps (such as neon lamps and neon signs, mercury-vapor lamps, etc.), and flames (light from the hot gas itself—so, for example, sodium in a gas flame emits characteristic yellow light). Emission can also be stimulated, as in a laser or a microwave maser.
Deceleration of a free charged particle, such as an electron, can produce visible radiation: cyclotron radiation, synchrotron radiation, and bremsstrahlung radiation are all examples of this. Particles moving through a medium faster than the speed of light in that medium can produce visible Cherenkov radiation. Certain chemicals produce visible radiation by chemoluminescence. In living things, this process is called bioluminescence. For example, fireflies produce light by this means, and boats moving through water can disturb plankton which produce a glowing wake.
Certain substances produce light when they are illuminated by more energetic radiation, a process known as fluorescence. Some substances emit light slowly after excitation by more energetic radiation. This is known as phosphorescence. Phosphorescent materials can also be excited by bombarding them with subatomic particles. Cathodoluminescence is one example. This mechanism is used in cathode ray tube television sets and computer monitors.
Certain other mechanisms can produce light:
- Bioluminescence
- Cherenkov radiation
- Electroluminescence
- Scintillation
- Sonoluminescence
- Triboluminescence
When the concept of light is intended to include very-high-energy photons (gamma rays), additional generation mechanisms include:
- Particle–antiparticle annihilation
- Radioactive decay
Units and measures
Light is measured with two main alternative sets of units: radiometry consists of measurements of light power at all wavelengths, while photometry measures light with wavelength weighted with respect to a standardized model of human brightness perception. Photometry is useful, for example, to quantify Illumination (lighting) intended for human use. The SI units for both systems are summarized in the following tables.
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 1] | Name | Symbol | Symbol | ||||
| Radiant energy | Qe[nb 2] | joule | J | M⋅L2⋅T−2 | Energy of electromagnetic radiation. | |||
| Radiant energy density | we | joule per cubic metre | J/m3 | M⋅L−1⋅T−2 | Radiant energy per unit volume. | |||
| Radiant flux | Φe[nb 2] | watt | W = J/s | M⋅L2⋅T−3 | Radiant energy emitted, reflected, transmitted or received, per unit time. This is sometimes also called "radiant power". | |||
| Spectral flux | Φe,ν[nb 3] | watt per hertz | W/Hz | M⋅L2⋅T−2 | Radiant flux per unit frequency or wavelength. The latter is commonly measured in W⋅nm−1. | |||
| Φe,λ[nb 4] | watt per metre | W/m | M⋅L⋅T−3 | |||||
| Radiant intensity | Ie,Ω[nb 5] | watt per steradian | W/sr | M⋅L2⋅T−3 | Radiant flux emitted, reflected, transmitted or received, per unit solid angle. This is a directional quantity. | |||
| Spectral intensity | Ie,Ω,ν[nb 3] | watt per steradian per hertz | W⋅sr−1⋅Hz−1 | M⋅L2⋅T−2 | Radiant intensity per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅nm−1. This is a directional quantity. | |||
| Ie,Ω,λ[nb 4] | watt per steradian per metre | W⋅sr−1⋅m−1 | M⋅L⋅T−3 | |||||
| Radiance | Le,Ω[nb 5] | watt per steradian per square metre | W⋅sr−1⋅m−2 | M⋅T−3 | Radiant flux emitted, reflected, transmitted or received by a surface, per unit solid angle per unit projected area. This is a directional quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral radiance | Le,Ω,ν[nb 3] | watt per steradian per square metre per hertz | W⋅sr−1⋅m−2⋅Hz−1 | M⋅T−2 | Radiance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅sr−1⋅m−2⋅nm−1. This is a directional quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Le,Ω,λ[nb 4] | watt per steradian per square metre, per metre | W⋅sr−1⋅m−3 | M⋅L−1⋅T−3 | |||||
| Irradiance Flux density |
Ee[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux received by a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral irradiance Spectral flux density |
Ee,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Irradiance of a surface per unit frequency or wavelength. This is sometimes also confusingly called "spectral intensity". Non-SI units of spectral flux density include jansky (1 Jy = 10−26 W⋅m−2⋅Hz−1) and solar flux unit (1 sfu = 10−22 W⋅m−2⋅Hz−1 = 104 Jy). | |||
| Ee,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiosity | Je[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux leaving (emitted, reflected and transmitted by) a surface per unit area. This is sometimes also confusingly called "intensity". | |||
| Spectral radiosity | Je,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiosity of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. This is sometimes also confusingly called "spectral intensity". | |||
| Je,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exitance | Me[nb 2] | watt per square metre | W/m2 | M⋅T−3 | Radiant flux emitted by a surface per unit area. This is the emitted component of radiosity. "Radiant emittance" is an old term for this quantity. This is sometimes also confusingly called "intensity". | |||
| Spectral exitance | Me,ν[nb 3] | watt per square metre per hertz | W⋅m−2⋅Hz−1 | M⋅T−2 | Radiant exitance of a surface per unit frequency or wavelength. The latter is commonly measured in W⋅m−2⋅nm−1. "Spectral emittance" is an old term for this quantity. This is sometimes also confusingly called "spectral intensity". | |||
| Me,λ[nb 4] | watt per square metre, per metre | W/m3 | M⋅L−1⋅T−3 | |||||
| Radiant exposure | He | joule per square metre | J/m2 | M⋅T−2 | Radiant energy received by a surface per unit area, or equivalently irradiance of a surface integrated over time of irradiation. This is sometimes also called "radiant fluence". | |||
| Spectral exposure | He,ν[nb 3] | joule per square metre per hertz | J⋅m−2⋅Hz−1 | M⋅T−1 | Radiant exposure of a surface per unit frequency or wavelength. The latter is commonly measured in J⋅m−2⋅nm−1. This is sometimes also called "spectral fluence". | |||
| He,λ[nb 4] | joule per square metre, per metre | J/m3 | M⋅L−1⋅T−2 | |||||
| Hemispherical emissivity | ε | N/A | 1 | Radiant exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Spectral hemispherical emissivity | εν or ελ |
N/A | 1 | Spectral exitance of a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Directional emissivity | εΩ | N/A | 1 | Radiance emitted by a surface, divided by that emitted by a black body at the same temperature as that surface. | ||||
| Spectral directional emissivity | εΩ,ν or εΩ,λ |
N/A | 1 | Spectral radiance emitted by a surface, divided by that of a black body at the same temperature as that surface. | ||||
| Hemispherical absorptance | A | N/A | 1 | Radiant flux absorbed by a surface, divided by that received by that surface. This should not be confused with "absorbance". | ||||
| Spectral hemispherical absorptance | Aν or Aλ |
N/A | 1 | Spectral flux absorbed by a surface, divided by that received by that surface. This should not be confused with "spectral absorbance". | ||||
| Directional absorptance | AΩ | N/A | 1 | Radiance absorbed by a surface, divided by the radiance incident onto that surface. This should not be confused with "absorbance". | ||||
| Spectral directional absorptance | AΩ,ν or AΩ,λ |
N/A | 1 | Spectral radiance absorbed by a surface, divided by the spectral radiance incident onto that surface. This should not be confused with "spectral absorbance". | ||||
| Hemispherical reflectance | R | N/A | 1 | Radiant flux reflected by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical reflectance | Rν or Rλ |
N/A | 1 | Spectral flux reflected by a surface, divided by that received by that surface. | ||||
| Directional reflectance | RΩ | N/A | 1 | Radiance reflected by a surface, divided by that received by that surface. | ||||
| Spectral directional reflectance | RΩ,ν or RΩ,λ |
N/A | 1 | Spectral radiance reflected by a surface, divided by that received by that surface. | ||||
| Hemispherical transmittance | T | N/A | 1 | Radiant flux transmitted by a surface, divided by that received by that surface. | ||||
| Spectral hemispherical transmittance | Tν or Tλ |
N/A | 1 | Spectral flux transmitted by a surface, divided by that received by that surface. | ||||
| Directional transmittance | TΩ | N/A | 1 | Radiance transmitted by a surface, divided by that received by that surface. | ||||
| Spectral directional transmittance | TΩ,ν or TΩ,λ |
N/A | 1 | Spectral radiance transmitted by a surface, divided by that received by that surface. | ||||
| Hemispherical attenuation coefficient | μ | reciprocal metre | m−1 | L−1 | Radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral hemispherical attenuation coefficient | μν or μλ |
reciprocal metre | m−1 | L−1 | Spectral radiant flux absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Directional attenuation coefficient | μΩ | reciprocal metre | m−1 | L−1 | Radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| Spectral directional attenuation coefficient | μΩ,ν or μΩ,λ |
reciprocal metre | m−1 | L−1 | Spectral radiance absorbed and scattered by a volume per unit length, divided by that received by that volume. | |||
| See also: SI · Radiometry · Photometry · (Compare) | ||||||||
| Quantity | Unit | Dimension | Notes | |||||
|---|---|---|---|---|---|---|---|---|
| Name | Symbol[nb 6] | Name | Symbol | Symbol[nb 7] | ||||
| Luminous energy | Qv[nb 8] | lumen second | lm⋅s | T J | The lumen second is sometimes called the talbot. | |||
| Luminous flux, luminous power | Φv[nb 8] | lumen (= candela steradians) | lm (= cd⋅sr) | J | Luminous energy per unit time | |||
| Luminous intensity | Iv | candela (= lumen per steradian) | cd (= lm/sr) | J | Luminous flux per unit solid angle | |||
| Luminance | Lv | candela per square metre | cd/m2 | L−2J | Luminous flux per unit solid angle per unit projected source area. The candela per square metre is sometimes called the nit. | |||
| Illuminance | Ev | lux (= lumen per square metre) | lx (= lm/m2) | L−2J | Luminous flux incident on a surface | |||
| Luminous exitance, luminous emittance | Mv | lumen per square metre | lm/m2 | L−2J | Luminous flux emitted from a surface | |||
| Luminous exposure | Hv | lux second | lx⋅s | L−2T J | Time-integrated illuminance | |||
| Luminous energy density | ωv | lumen second per cubic metre | lm⋅s/m3 | L−3T J | ||||
| Luminous efficacy (of radiation) | K | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to radiant flux | |||
| Luminous efficacy (of a source) | η[nb 8] | lumen per watt | lm/W | M−1L−2T3J | Ratio of luminous flux to power consumption | |||
| Luminous efficiency, luminous coefficient | V | 1 | Luminous efficacy normalized by the maximum possible efficacy | |||||
| See also: SI · Photometry · Radiometry · (Compare) | ||||||||
The photometry units are different from most systems of physical units in that they take into account how the human eye responds to light. The cone cells in the human eye are of three types which respond differently across the visible spectrum, and the cumulative response peaks at a wavelength of around 555 nm. Therefore, two sources of light which produce the same intensity (W/m2) of visible light do not necessarily appear equally bright. The photometry units are designed to take this into account, and therefore are a better representation of how "bright" a light appears to be than raw intensity. They relate to raw power by a quantity called luminous efficacy, and are used for purposes like determining how to best achieve sufficient illumination for various tasks in indoor and outdoor settings. The illumination measured by a photocell sensor does not necessarily correspond to what is perceived by the human eye, and without filters which may be costly, photocells and charge-coupled devices (CCD) tend to respond to some infrared, ultraviolet or both.
Light pressure
Light exerts physical pressure on objects in its path, a phenomenon which can be deduced by Maxwell's equations, but can be more easily explained by the particle nature of light: photons strike and transfer their momentum. Light pressure is equal to the power of the light beam divided by c, the speed of light. Due to the magnitude of c, the effect of light pressure is negligible for everyday objects. For example, a one-milliwatt laser pointer exerts a force of about 3.3 piconewtons on the object being illuminated; thus, one could lift a U.S. penny with laser pointers, but doing so would require about 30 billion 1-mW laser pointers.[20] However, in nanometre-scale applications such as nanoelectromechanical systems (NEMS), the effect of light pressure is more significant, and exploiting light pressure to drive NEMS mechanisms and to flip nanometre-scale physical switches in integrated circuits is an active area of research.[21] At larger scales, light pressure can cause asteroids to spin faster,[22] acting on their irregular shapes as on the vanes of a windmill. The possibility of making solar sails that would accelerate spaceships in space is also under investigation.[23][24]
Although the motion of the Crookes radiometer was originally attributed to light pressure, this interpretation is incorrect; the characteristic Crookes rotation is the result of a partial vacuum.[25] This should not be confused with the Nichols radiometer, in which the (slight) motion caused by torque (though not enough for full rotation against friction) is directly caused by light pressure.[26] As a consequence of light pressure, Einstein[27] in 1909 predicted the existence of "radiation friction" which would oppose the movement of matter. He wrote, "radiation will exert pressure on both sides of the plate. The forces of pressure exerted on the two sides are equal if the plate is at rest. However, if it is in motion, more radiation will be reflected on the surface that is ahead during the motion (front surface) than on the back surface. The backwardacting force of pressure exerted on the front surface is thus larger than the force of pressure acting on the back. Hence, as the resultant of the two forces, there remains a force that counteracts the motion of the plate and that increases with the velocity of the plate. We will call this resultant 'radiation friction' in brief."
Usually light momentum is aligned with its direction of motion. However, for example in evanescent waves momentum is transverse to direction of propagation.[28]
Historical theories about light, in chronological order
Classical Greece and Hellenism
In the fifth century BC, Empedocles postulated that everything was composed of four elements; fire, air, earth and water. He believed that Aphrodite made the human eye out of the four elements and that she lit the fire in the eye which shone out from the eye making sight possible. If this were true, then one could see during the night just as well as during the day, so Empedocles postulated an interaction between rays from the eyes and rays from a source such as the sun.[29]
In about 300 BC, Euclid wrote Optica, in which he studied the properties of light. Euclid postulated that light travelled in straight lines and he described the laws of reflection and studied them mathematically. He questioned that sight is the result of a beam from the eye, for he asks how one sees the stars immediately, if one closes one's eyes, then opens them at night. If the beam from the eye travels infinitely fast this is not a problem.[30]
In 55 BC, Lucretius, a Roman who carried on the ideas of earlier Greek atomists, wrote that "The light & heat of the sun; these are composed of minute atoms which, when they are shoved off, lose no time in shooting right across the interspace of air in the direction imparted by the shove." (from On the nature of the Universe). Despite being similar to later particle theories, Lucretius's views were not generally accepted. Ptolemy (c. 2nd century) wrote about the refraction of light in his book Optics.[31]
Classical India
In ancient India, the Hindu schools of Samkhya and Vaisheshika, from around the early centuries AD developed theories on light. According to the Samkhya school, light is one of the five fundamental "subtle" elements (tanmatra) out of which emerge the gross elements. The atomicity of these elements is not specifically mentioned and it appears that they were actually taken to be continuous.[32] On the other hand, the Vaisheshika school gives an atomic theory of the physical world on the non-atomic ground of ether, space and time. (See Indian atomism.) The basic atoms are those of earth (prthivi), water (pani), fire (agni), and air (vayu) Light rays are taken to be a stream of high velocity of tejas (fire) atoms. The particles of light can exhibit different characteristics depending on the speed and the arrangements of the tejas atoms. The Vishnu Purana refers to sunlight as "the seven rays of the sun".[32]
The Indian Buddhists, such as Dignāga in the 5th century and Dharmakirti in the 7th century, developed a type of atomism that is a philosophy about reality being composed of atomic entities that are momentary flashes of light or energy. They viewed light as being an atomic entity equivalent to energy.[32]
Descartes
René Descartes (1596–1650) held that light was a mechanical property of the luminous body, rejecting the "forms" of Ibn al-Haytham and Witelo as well as the "species" of Bacon, Grosseteste, and Kepler.[33] In 1637 he published a theory of the refraction of light that assumed, incorrectly, that light travelled faster in a denser medium than in a less dense medium. Descartes arrived at this conclusion by analogy with the behaviour of sound waves. Although Descartes was incorrect about the relative speeds, he was correct in assuming that light behaved like a wave and in concluding that refraction could be explained by the speed of light in different media.
Descartes is not the first to use the mechanical analogies but because he clearly asserts that light is only a mechanical property of the luminous body and the transmitting medium, Descartes' theory of light is regarded as the start of modern physical optics.[33]
Particle theory
Pierre Gassendi (1592–1655), an atomist, proposed a particle theory of light which was published posthumously in the 1660s. Isaac Newton studied Gassendi's work at an early age, and preferred his view to Descartes' theory of the plenum. He stated in his Hypothesis of Light of 1675 that light was composed of corpuscles (particles of matter) which were emitted in all directions from a source. One of Newton's arguments against the wave nature of light was that waves were known to bend around obstacles, while light travelled only in straight lines. He did, however, explain the phenomenon of the diffraction of light (which had been observed by Francesco Grimaldi) by allowing that a light particle could create a localised wave in the aether.
Newton's theory could be used to predict the reflection of light, but could only explain refraction by incorrectly assuming that light accelerated upon entering a denser medium because the gravitational pull was greater. Newton published the final version of his theory in his Opticks of 1704. His reputation helped the particle theory of light to hold sway during the 18th century. The particle theory of light led Laplace to argue that a body could be so massive that light could not escape from it. In other words, it would become what is now called a black hole. Laplace withdrew his suggestion later, after a wave theory of light became firmly established as the model for light (as has been explained, neither a particle or wave theory is fully correct). A translation of Newton's essay on light appears in The large scale structure of space-time, by Stephen Hawking and George F. R. Ellis.
The fact that light could be polarized was for the first time qualitatively explained by Newton using the particle theory. Étienne-Louis Malus in 1810 created a mathematical particle theory of polarization. Jean-Baptiste Biot in 1812 showed that this theory explained all known phenomena of light polarization. At that time the polarization was considered as the proof of the particle theory.
Wave theory
To explain the origin of colors, Robert Hooke (1635–1703) developed a "pulse theory" and compared the spreading of light to that of waves in water in his 1665 work Micrographia ("Observation IX"). In 1672 Hooke suggested that light's vibrations could be perpendicular to the direction of propagation. Christiaan Huygens (1629–1695) worked out a mathematical wave theory of light in 1678, and published it in his Treatise on light in 1690. He proposed that light was emitted in all directions as a series of waves in a medium called the Luminiferous ether. As waves are not affected by gravity, it was assumed that they slowed down upon entering a denser medium.[34]

The wave theory predicted that light waves could interfere with each other like sound waves (as noted around 1800 by Thomas Young). Young showed by means of a diffraction experiment that light behaved as waves. He also proposed that different colors were caused by different wavelengths of light, and explained color vision in terms of three-colored receptors in the eye. Another supporter of the wave theory was Leonhard Euler. He argued in Nova theoria lucis et colorum (1746) that diffraction could more easily be explained by a wave theory. In 1816 André-Marie Ampère gave Augustin-Jean Fresnel an idea that the polarization of light can be explained by the wave theory if light were a transverse wave.[35]
Later, Fresnel independently worked out his own wave theory of light, and presented it to the Académie des Sciences in 1817. Siméon Denis Poisson added to Fresnel's mathematical work to produce a convincing argument in favor of the wave theory, helping to overturn Newton's corpuscular theory. By the year 1821, Fresnel was able to show via mathematical methods that polarization could be explained by the wave theory of light if and only if light was entirely transverse, with no longitudinal vibration whatsoever.
The weakness of the wave theory was that light waves, like sound waves, would need a medium for transmission. The existence of the hypothetical substance luminiferous aether proposed by Huygens in 1678 was cast into strong doubt in the late nineteenth century by the Michelson–Morley experiment.
Newton's corpuscular theory implied that light would travel faster in a denser medium, while the wave theory of Huygens and others implied the opposite. At that time, the speed of light could not be measured accurately enough to decide which theory was correct. The first to make a sufficiently accurate measurement was Léon Foucault, in 1850.[36] His result supported the wave theory, and the classical particle theory was finally abandoned, only to partly re-emerge in the 20th century.
Electromagnetic theory
In 1845, Michael Faraday discovered that the plane of polarization of linearly polarized light is rotated when the light rays travel along the magnetic field direction in the presence of a transparent dielectric, an effect now known as Faraday rotation.[37] This was the first evidence that light was related to electromagnetism. In 1846 he speculated that light might be some form of disturbance propagating along magnetic field lines.[37] Faraday proposed in 1847 that light was a high-frequency electromagnetic vibration, which could propagate even in the absence of a medium such as the ether.[38]
Faraday's work inspired James Clerk Maxwell to study electromagnetic radiation and light. Maxwell discovered that self-propagating electromagnetic waves would travel through space at a constant speed, which happened to be equal to the previously measured speed of light. From this, Maxwell concluded that light was a form of electromagnetic radiation: he first stated this result in 1862 in On Physical Lines of Force. In 1873, he published A Treatise on Electricity and Magnetism, which contained a full mathematical description of the behavior of electric and magnetic fields, still known as Maxwell's equations. Soon after, Heinrich Hertz confirmed Maxwell's theory experimentally by generating and detecting radio waves in the laboratory, and demonstrating that these waves behaved exactly like visible light, exhibiting properties such as reflection, refraction, diffraction, and interference. Maxwell's theory and Hertz's experiments led directly to the development of modern radio, radar, television, electromagnetic imaging, and wireless communications.
In the quantum theory, photons are seen as wave packets of the waves described in the classical theory of Maxwell. The quantum theory was needed to explain effects even with visual light that Maxwell's classical theory could not (such as spectral lines).
Quantum theory
In 1900 Max Planck, attempting to explain black-body radiation, suggested that although light was a wave, these waves could gain or lose energy only in finite amounts related to their frequency. Planck called these "lumps" of light energy "quanta" (from a Latin word for "how much"). In 1905, Albert Einstein used the idea of light quanta to explain the photoelectric effect, and suggested that these light quanta had a "real" existence. In 1923 Arthur Holly Compton showed that the wavelength shift seen when low intensity X-rays scattered from electrons (so called Compton scattering) could be explained by a particle-theory of X-rays, but not a wave theory. In 1926 Gilbert N. Lewis named these light quanta particles photons.[39]
Eventually the modern theory of quantum mechanics came to picture light as (in some sense) both a particle and a wave, and (in another sense), as a phenomenon which is neither a particle nor a wave (which actually are macroscopic phenomena, such as baseballs or ocean waves). Instead, modern physics sees light as something that can be described sometimes with mathematics appropriate to one type of macroscopic metaphor (particles), and sometimes another macroscopic metaphor (water waves), but is actually something that cannot be fully imagined. As in the case for radio waves and the X-rays involved in Compton scattering, physicists have noted that electromagnetic radiation tends to behave more like a classical wave at lower frequencies, but more like a classical particle at higher frequencies, but never completely loses all qualities of one or the other. Visible light, which occupies a middle ground in frequency, can easily be shown in experiments to be describable using either a wave or particle model, or sometimes both.
In February 2018, scientists reported, for the first time, the discovery of a new form of light, which may involve polaritons, that could be useful in the development of quantum computers.[40][41]
See also
- Automotive lighting
- Ballistic photon
- Color temperature
- Fermat's principle
- Huygens' principle
- Journal of Luminescence
- Light art
- Light beam – in particular about light beams visible from the side
- Light Fantastic (TV series)
- Light mill
- Light painting
- Light pollution
- Light therapy
- Lighting
- List of light sources
- Luminescence: The Journal of Biological and Chemical Luminescence
- Photic sneeze reflex
- Right to light
- Risks and benefits of sun exposure
- Spectroscopy
Notes
- Standards organizations recommend that radiometric quantities should be denoted with suffix "e" (for "energetic") to avoid confusion with photometric or photon quantities.
- Alternative symbols sometimes seen: W or E for radiant energy, P or F for radiant flux, I for irradiance, W for radiant exitance.
- Spectral quantities given per unit frequency are denoted with suffix "ν" (Greek)—not to be confused with suffix "v" (for "visual") indicating a photometric quantity.
- Spectral quantities given per unit wavelength are denoted with suffix "λ" (Greek).
- Directional quantities are denoted with suffix "Ω" (Greek).
- Standards organizations recommend that photometric quantities be denoted with a subscript "v" (for "visual") to avoid confusion with radiometric or photon quantities. For example: USA Standard Letter Symbols for Illuminating Engineering USAS Z7.1-1967, Y10.18-1967
- The symbols in this column denote dimensions; "L", "T" and "J" are for length, time and luminous intensity respectively, not the symbols for the units litre, tesla and joule.
- Alternative symbols sometimes seen: W for luminous energy, P or F for luminous flux, and ρ for luminous efficacy of a source.
References
- CIE (1987). International Lighting Vocabulary Archived 27 February 2010 at the Wayback Machine. Number 17.4. CIE, 4th edition. ISBN 978-3-900734-07-7.
By the International Lighting Vocabulary, the definition of light is: "Any radiation capable of causing a visual sensation directly." - Pal, G.K.; Pal, Pravati (2001). "chapter 52". Textbook of Practical Physiology (1st ed.). Chennai: Orient Blackswan. p. 387. ISBN 978-81-250-2021-9. Retrieved 11 October 2013.
The human eye has the ability to respond to all the wavelengths of light from 400–700 nm. This is called the visible part of the spectrum.
- Buser, Pierre A.; Imbert, Michel (1992). Vision. MIT Press. p. 50. ISBN 978-0-262-02336-8. Retrieved 11 October 2013.
Light is a special class of radiant energy embracing wavelengths between 400 and 700 nm (or mμ), or 4000 to 7000 Å.
- Uzan, J-P; Leclercq, B (2008). The Natural Laws of the Universe. The Natural Laws of the Universe: Understanding Fundamental Constants. pp. 43–4. Bibcode:2008nlu..book.....U. doi:10.1007/978-0-387-74081-2. ISBN 978-0-387-73454-5.
- Gregory Hallock Smith (2006). Camera lenses: from box camera to digital. SPIE Press. p. 4. ISBN 978-0-8194-6093-6.
- Narinder Kumar (2008). Comprehensive Physics XII. Laxmi Publications. p. 1416. ISBN 978-81-7008-592-8.
- Laufer, Gabriel (13 July 1996). Introduction to Optics and Lasers in Engineering. Introduction to Optics and Lasers in Engineering. p. 11. Bibcode:1996iole.book.....L. ISBN 978-0-521-45233-5. Retrieved 20 October 2013.
- Bradt, Hale (2004). Astronomy Methods: A Physical Approach to Astronomical Observations. Cambridge University Press. p. 26. ISBN 978-0-521-53551-9. Retrieved 20 October 2013.
- Ohannesian, Lena; Streeter, Anthony (9 November 2001). Handbook of Pharmaceutical Analysis. CRC Press. p. 187. ISBN 978-0-8247-4194-5. Retrieved 20 October 2013.
- Ahluwalia, V.K.; Goyal, Madhuri (1 January 2000). A Textbook of Organic Chemistry. Narosa. p. 110. ISBN 978-81-7319-159-6. Retrieved 20 October 2013.
- Sliney, David H.; Wangemann, Robert T.; Franks, James K.; Wolbarsht, Myron L. (1976). "Visual sensitivity of the eye to infrared laser radiation". Journal of the Optical Society of America. 66 (4): 339–341. Bibcode:1976JOSA...66..339S. doi:10.1364/JOSA.66.000339. PMID 1262982.
The foveal sensitivity to several near-infrared laser wavelengths was measured. It was found that the eye could respond to radiation at wavelengths at least as far as 1064 nm. A continuous 1064 nm laser source appeared red, but a 1060 nm pulsed laser source appeared green, which suggests the presence of second harmonic generation in the retina.
- Lynch, David K.; Livingston, William Charles (2001). Color and Light in Nature (2nd ed.). Cambridge: Cambridge University Press. p. 231. ISBN 978-0-521-77504-5. Retrieved 12 October 2013.
Limits of the eye's overall range of sensitivity extends from about 310 to 1050 nanometers
- Dash, Madhab Chandra; Dash, Satya Prakash (2009). Fundamentals of Ecology 3E. Tata McGraw-Hill Education. p. 213. ISBN 978-1-259-08109-5. Retrieved 18 October 2013.
Normally the human eye responds to light rays from 390 to 760 nm. This can be extended to a range of 310 to 1,050 nm under artificial conditions.
- Saidman, Jean (15 May 1933). "Sur la visibilité de l'ultraviolet jusqu'à la longueur d'onde 3130" [The visibility of the ultraviolet to the wave length of 3130]. Comptes rendus de l'Académie des sciences (in French). 196: 1537–9.
- Oldford, R. W; MacKay, R. J (2000). "Scientific Method, Statistical Method and the Speed of Light". Statistical Science. 15 (3): 254–278. doi:10.1214/ss/1009212817. MR 1847825.
- Michelson, A.A. (January 1927). "Measurements of the velocity of light between Mount Wilson and Mount San Antonio". Astrophysical Journal. 65: 1. Bibcode:1927ApJ....65....1M. doi:10.1086/143021.
- Harvard News Office (24 January 2001). "Harvard Gazette: Researchers now able to stop, restart light". News.harvard.edu. Archived from the original on 28 October 2011. Retrieved 8 November 2011.
- "Spectrum and the Color Sensitivity of the Eye" (PDF). Thulescientific.com. Retrieved 29 August 2017.
- "Reference Solar Spectral Irradiance: Air Mass 1.5". Retrieved 12 November 2009.
- Tang, Hong (1 October 2009). "May The Force of Light Be With You". IEEE Spectrum. 46 (10): 46–51. doi:10.1109/MSPEC.2009.5268000.
- See, for example, nano-opto-mechanical systems research at Yale University.
- Kathy A. (5 February 2004). "Asteroids Get Spun By the Sun". Discover Magazine.
- "Solar Sails Could Send Spacecraft 'Sailing' Through Space". NASA. 31 August 2004.
- "NASA team successfully deploys two solar sail systems". NASA. 9 August 2004.
- P. Lebedev, Untersuchungen über die Druckkräfte des Lichtes, Ann. Phys. 6, 433 (1901).
- Nichols, E.F; Hull, G.F. (1903). "The Pressure due to Radiation". The Astrophysical Journal. 17 (5): 315–351. Bibcode:1903ApJ....17..315N. doi:10.1086/141035.
- Einstein, A. (1909). On the development of our views concerning the nature and constitution of radiation. Translated in: The Collected Papers of Albert Einstein, vol. 2 (Princeton University Press, Princeton, 1989). Princeton, New Jersey: Princeton University Press. p. 391.
- Antognozzi, M.; Bermingham, C. R.; Harniman, R. L.; Simpson, S.; Senior, J.; Hayward, R.; Hoerber, H.; Dennis, M. R.; Bekshaev, A. Y. (August 2016). "Direct measurements of the extraordinary optical momentum and transverse spin-dependent force using a nano-cantilever". Nature Physics. 12 (8): 731–735. arXiv:1506.04248. doi:10.1038/nphys3732. ISSN 1745-2473.
- Singh, S. (2009). Fundamentals of Optical Engineering. Discovery Publishing House. ISBN 9788183564366.
- O'Connor, J J; Robertson, E F (August 2002). "Light through the ages: Ancient Greece to Maxwell".
- Ptolemy and A. Mark Smith (1996). Ptolemy's Theory of Visual Perception: An English Translation of the Optics with Introduction and Commentary. Diane Publishing. p. 23. ISBN 978-0-87169-862-9.
- "Shastra Pratibha 2015 Seniors Booklet" (PDF). Sifuae.com. Retrieved 29 August 2017.
- Theories of light, from Descartes to Newton A.I. Sabra CUP Archive,1981 p. 48 ISBN 0-521-28436-8, 978-0-521-28436-3
- Fokko Jan Dijksterhuis, Lenses and Waves: Christiaan Huygens and the Mathematical Science of Optics in the 17th Century, Kluwer Academic Publishers, 2004, ISBN 1-4020-2697-8
- James R. Hofmann, André-Marie Ampère: Enlightenment and Electrodynamics, Cambridge University Press, 1996, p. 222.
- David Cassidy; Gerald Holton; James Rutherford (2002). Understanding Physics. Birkhäuser. ISBN 978-0-387-98756-9.
- Longair, Malcolm (2003). Theoretical Concepts in Physics. p. 87.
- Cassidy, D (2002). Understanding Physics. Springer Verlag New York.
-

- Hignett, Katherine (16 February 2018). "Physics Creates New Form of Light That Could Drive The Quantum Computing Revolution". Newsweek. Retrieved 17 February 2018.
- Liang, Qi-Yu; et al. (16 February 2018). "Observation of three-photon bound states in a quantum nonlinear medium". Science. 359 (6377): 783–786. arXiv:1709.01478. Bibcode:2018Sci...359..783L. doi:10.1126/science.aao7293. PMC 6467536. PMID 29449489.
External links
| Wikimedia Commons has media related to Light. |
| Look up light in Wiktionary, the free dictionary. |
| Wikiquote has quotations related to: Light |