2
2 (two) is a number, numeral, and glyph. It is the natural number following 1 and preceding 3. It is the smallest and only even prime number. Because it forms the basis of a duality, it has religious and spiritual significance in many cultures.
| ||||
|---|---|---|---|---|
[[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] [[{{#expr: (floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}} (number)|{{#switch:{{{1}}}|-1={{#ifexpr:(floor({{{number}}} div 10)) = 0|-1|←}}|10=→|#default={{#expr:(floor({{{number}}} div {{{factor}}})) * {{{factor}}}+({{{1}}}*{{{factor}}} div 10)}}}}]] | ||||
| Cardinal | two | |||
| Ordinal | 2nd (second / twoth) | |||
| Numeral system | binary | |||
| Factorization | prime | |||
| Gaussian integer factorization | ||||
| Prime | 1st | |||
| Divisors | 1, 2 | |||
| Greek numeral | Β´ | |||
| Roman numeral | II, ii | |||
| Greek prefix | di- | |||
| Latin prefix | duo- bi- | |||
| Old English prefix | twi- | |||
| Binary | 102 | |||
| Ternary | 23 | |||
| Quaternary | 24 | |||
| Quinary | 25 | |||
| Senary | 26 | |||
| Octal | 28 | |||
| Duodecimal | 212 | |||
| Hexadecimal | 216 | |||
| Vigesimal | 220 | |||
| Base 36 | 236 | |||
| Greek numeral | β' | |||
| Arabic, Kurdish, Persian, Sindhi, Urdu | ٢ | |||
| Ge'ez | ፪ | |||
| Bengali | ২ | |||
| Chinese numeral | 二,弍,貳 | |||
| Devanāgarī | २ | |||
| Telugu | ౨ | |||
| Tamil | ௨ | |||
| Kannada | ೨ | |||
| Hebrew | ב | |||
| Japanese numeral | 二/弐 | |||
| Khmer | ២ | |||
| Korean | 이,둘 | |||
| Thai | ๒ | |||
Evolution of the glyph
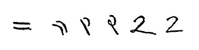
The glyph used in the modern Western world to represent the number 2 traces its roots back to the Indic Brahmic script, where "2" was written as two horizontal lines. The modern Chinese and Japanese languages still use this method. The Gupta script rotated the two lines 45 degrees, making them diagonal. The top line was sometimes also shortened and had its bottom end curve towards the center of the bottom line. In the Nagari script, the top line was written more like a curve connecting to the bottom line. In the Arabic Ghubar writing, the bottom line was completely vertical, and the glyph looked like a dotless closing question mark. Restoring the bottom line to its original horizontal position, but keeping the top line as a curve that connects to the bottom line leads to our modern glyph.[1]
In fonts with text figures, 2 usually is of x-height, for example, ![]()
In mathematics
An integer is called even if it is divisible by 2. For integers written in a numeral system based on an even number, such as decimal, hexadecimal, or in any other base that is even, divisibility by 2 is easily tested by merely looking at the last digit. If it is even, then the whole number is even. In particular, when written in the decimal system, all multiples of 2 will end in 0, 2, 4, 6, or 8.
Two is the smallest prime number, and the only even prime number (for this reason it is sometimes called "the oddest prime").[2] The next prime is three. Two and three are the only two consecutive prime numbers. 2 is the first Sophie Germain prime, the first factorial prime, the first Lucas prime, and the first Ramanujan prime.[3]
Two is the third (or fourth) Fibonacci number.
Two is the base of the binary system, the numeral system with the fewest tokens allowing to denote a natural number n substantially more concise (log2 n tokens), compared to a direct representation by the corresponding count of a single token (n tokens). This binary number system is used extensively in computing.
For any number x:
- x + x = 2 · x addition to multiplication
- x · x = x2 multiplication to exponentiation
- xx = x↑↑2 exponentiation to tetration
Extending this sequence of operations by introducing the notion of hyperoperations, here denoted by "hyper(a,b,c)" with a and c being the first and second operand, and b being the level in the above sketched sequence of operations, the following holds in general:
- hyper(x,n,x) = hyper(x,(n + 1),2).
Two has therefore the unique property that 2 + 2 = 2 · 2 = 22 = 2↑↑2 = 2↑↑↑2 = ..., disregarding the level of the hyperoperation, here denoted by Knuth's up-arrow notation. The number of up-arrows refers to the level of the hyperoperation.
Two is the only number x such that the sum of the reciprocals of the powers of x equals itself. In symbols
This comes from the fact that:
Powers of two are central to the concept of Mersenne primes, and important to computer science. Two is the first Mersenne prime exponent.
Taking the square root of a number is such a common mathematical operation, that the spot on the root sign where the exponent would normally be written for cubic and other roots, may simply be left blank for square roots, as it is tacitly understood.
The square root of 2 was the first known irrational number.
The smallest field has two elements.
In a set-theoretical construction of the natural numbers, 2 is identified with the set {{∅},∅}. This latter set is important in category theory: it is a subobject classifier in the category of sets.
Two also has the unique property such that
and also
for a not equal to zero
In any n-dimensional, euclidean space two distinct points determine a line.
For any polyhedron homeomorphic to a sphere, the Euler characteristic is χ = V − E + F = 2, where V is the number of vertices, E is the number of edges, and F is the number of faces.
In science
- The number of polynucleotide strands in a DNA double helix.[4]
- The first magic number.[5]
- The atomic number of helium.[6]
- The atomic mass of deuterium, an isotope of hydrogen.
- The ASCII code of "Start of Text".
- 2 Pallas, a large asteroid in the main belt and the second asteroid ever to be discovered.[7]
- The Roman numeral II (usually) stands for the second-discovered satellite of a planet or minor planet (e.g. Pluto II or (87) Sylvia II Remus).
- A binary star is a stellar system consisting of two stars orbiting around their center of mass.[8]
- The number of brain and cerebellar hemispheres.[9]
Other

In pre-1972 Indonesian and Malay orthography, 2 was shorthand for the reduplication that forms plurals: orang "person", orang-orang or orang2 "people". In Astrology, Taurus is the second sign of the Zodiac.
References
- Georges Ifrah, The Universal History of Numbers: From Prehistory to the Invention of the Computer transl. David Bellos et al. London: The Harvill Press (1998): 393, Fig. 24.62
- John Horton Conway & Richard K. Guy, The Book of Numbers. New York: Springer (1996): 25. ISBN 0-387-97993-X. "Two is celebrated as the only even prime, which in some sense makes it the oddest prime of all."
- "Sloane's A104272 : Ramanujan primes". The On-Line Encyclopedia of Integer Sequences. OEIS Foundation. Retrieved 2016-06-01.
- "Double-stranded DNA". Scitable. Nature Education. Retrieved 2019-12-22.
- "The Complete Explanation of the Nuclear Magic Numbers Which Indicate the Filling of Nucleonic Shells and the Revelation of Special Numbers Indicating the Filling of Subshells Within Those Shells". www.sjsu.edu. Retrieved 2019-12-22.
- Bezdenezhnyi, V. P. (2004). "Nuclear Isotopes and Magic Numbers". Odessa Astronomical Publications. 17: 11. Bibcode:2004OAP....17...11B.
- "Asteroid Fact Sheet". nssdc.gsfc.nasa.gov. Retrieved 2019-12-22.
- Staff (2018-01-17). "Binary Star Systems: Classification and Evolution". Space.com. Retrieved 2019-12-22.
- Lewis, Tanya (2018-09-28). "Human Brain: Facts, Functions & Anatomy". livescience.com. Retrieved 2019-12-22.
External links
| Wikimedia Commons has media related to: |
| Look up two or both in Wiktionary, the free dictionary. |
