Revised Julian calendar

The Revised Julian calendar, also known as the Milanković calendar, or, less formally, new calendar, is a calendar proposed by the Serbian scientist Milutin Milanković in 1923, which effectively discontinued the 340 years of divergence between the naming of dates sanctioned by those Eastern Orthodox churches adopting it and the Gregorian calendar that has come to predominate worldwide. This calendar was intended to replace the ecclesiastical calendar based on the Julian calendar hitherto in use by all of the Eastern Orthodox Church. From 1 March 1600 through 28 February 2800, the Revised Julian calendar aligns its dates with the Gregorian calendar, which was proclaimed in 1582 by Pope Gregory XIII for adoption by the Christian world.[1] The calendar has been adopted by the Orthodox churches of Constantinople, Albania, Alexandria, Antioch, Bulgaria, Cyprus, Greece, and Romania.

The Revised Julian calendar has the same months and month lengths as the Julian calendar, but, in the Revised Julian calendar, years evenly divisible by 100 are not leap years, except that years with remainders of 200 or 600 when divided by 900 remain leap years, e.g. 2000 and 2400 as in the Gregorian Calendar.[2]

Implementation
Century
year		Remain-
der on
divide
by 900		Is a
Revised
Julian
leap
year		Is a
Grego-
rian
leap
year		Revised
Julian is
same as
Grego-
rian
1000100✗✗✓
1100200✓✗✗
1200300✗✓✗
1300400✗✗✓
1400500✗✗✓
1500600✓✗✗
1600700✗✓✗
1700800✗✗✓
18000✗✗✓
1900100✗✗✓
2000200✓✓✓
2100300✗✗✓
2200400✗✗✓
2300500✗✗✓
2400600✓✓✓
2500700✗✗✓
2600800✗✗✓
27000✗✗✓
2800100✗✓✗
2900200✓✗✗
3000300✗✗✓
3100400✗✗✓
3200500✗✓✗
3300600✓✗✗
3400700✗✗✓
3500800✗✗✓
36000✗✓✗
3700100✗✗✓
3800200✓✗✗
3900300✗✗✓
4000400✗✓✗

 Comparison of Revised Julian and Gregorian
calendar century years. (In the original Julian
calendar, every century year is a leap year.)

A committee composed of members of the Greek government and Greek Orthodox Church was set up to look into the question of calendar reform. It reported in January 1923.[3] It recommended a switch (for civil purposes only) to the "political calendar" devised in 1785 and advocated by Maksim Trpković.[4] Trpković advocated this calendar in preference to the Gregorian because of its greater accuracy and also because the vernal equinox would generally fall on 21 March, the date allocated to it by the church. In the Gregorian, it generally falls on 20 March. As in the Gregorian, end-century years are generally not leap years, but years that give remainder 0 or 400 on division by 900 were to be leap years. The changeover went into effect on 17 February/1 March.

After the promulgation of the royal decree, the Ecumenical Patriarch, Patriarch Meletius IV of Constantinople, issued an encyclical on 3 February recommending the calendar's adoption by Orthodox churches. The matter came up for discussion at a "Pan-Orthodox" Congress of Constantinople, which deliberated in May and June. Subsequently, it was adopted by several of the autocephalous Orthodox churches. The synod was chaired by the controversial patriarch and representatives were present from the churches of Cyprus, Greece, Romania and Serbia. There were no representatives of the other members of the original Orthodox Pentarchy (the Patriarchates of Jerusalem, Antioch, and Alexandria) or from the largest Orthodox church, the Russian Orthodox Church.[5]

Discussion was lengthy because although Serbia officially supported the political calendar, Milanković (an astronomical delegate to the synod representing the Kingdom of Serbs, Croats and Slovenes) pressed for the adoption of his own version, in which the centennial leap years would be those giving remainder 200 or 600 when divided by 900 and the equinox would generally fall on 20 March (as in the Gregorian). Under the official proposal the equinox would sometimes fall on 22 March. This might make Easter fall outside its canonical limits due to the requirement that the Easter full moon follow the equinox.[6] Also his scheme maximised the time during which the political calendar and the Gregorian would run in tandem.

Milanković's arguments won the day. In its decision the conference noted that "the difference between the length of the political year of the new calendar and the Gregorian is so small that only after 877 years it is observed difference of dates." The same decision provided that the coming 1 October should be called 14 October, thus dropping thirteen days. It then adopted the leap year rule of Milanković.[7][8] The political calendar was preferred over the Gregorian because its mean year was within two seconds of the then current length of the mean tropical year.[8] The present vernal equinox year, however, is about 12 seconds longer, in terms of mean solar days.

The synod also proposed the adoption of an astronomical rule for Easter: Easter was to be the Sunday after the midnight-to-midnight day at the meridian of the Church of the Holy Sepulchre in Jerusalem (35°13′47.2″ E or UT+2h20m55s for the small dome) during which the first full moon after the vernal equinox occurs. Although the instant of the full moon must occur after the instant of the vernal equinox, it may occur on the same day. If the full moon occurs on a Sunday, Easter is the following Sunday. Churches that adopted this calendar did so on varying dates. However, all Eastern Orthodox churches continue to use the Julian calendar to determine the date of Easter (except for the Finnish Orthodox Church and the Estonian Orthodox Church, which now use the Gregorian Easter).

Arithmetic

The following are Gregorian minus Revised Julian date differences, calculated for the beginning of January and March in each century year, which is where differences arise or disappear, until AD 10000. These are exact arithmetic calculations, not depending on any astronomy. A negative difference means that the proleptic Revised Julian calendar was behind the proleptic Gregorian calendar. The Revised Julian calendar is the same as the Gregorian calendar from 1 March 1600 to 28 February 2800, but the following day would be 1 March 2800 (RJ) or 29 February 2800 (G); this difference is denoted as '+1' in the table. 2900 is a leap year in Revised Julian, but not Gregorian: 29 February 2900 (RJ) is the same as 28 February 2900 (G) and the next day will be 1 March 2900 in both calendars - hence the '0' notation.

Revised Julian (RJ) minus Gregorian (G) date differences
Dates RJ − G Dates RJ − G Dates RJ − G
Mar BC 1 – Feb AD 2000Mar AD 3600 – Feb AD 3800+1Mar AD 7200 – Feb AD 7400+2
Mar AD 200 – Feb AD 400−1Mar AD 3800 – Feb AD 40000Mar AD 7400 – Feb AD 7600+1
Mar AD 400 – Feb AD 6000Mar AD 4000 – Feb AD 4200+1Mar AD 7600 – Feb AD 7800+2
Mar AD 600 – Feb AD 800−1Mar AD 4200 – Feb AD 44000Mar AD 7800 – Feb AD 8000+1
Mar AD 800 – Feb AD 11000Mar AD 4400 – Feb AD 4700+1Mar AD 8000 – Feb AD 8300+2
Mar AD 1100 – Feb AD 1200−1Mar AD 4700 – Feb AD 48000Mar AD 8300 – Feb AD 8400+1
Mar AD 1200 – Feb AD 15000Mar AD 4800 – Feb AD 5100+1Mar AD 8400 – Feb AD 8700+2
Mar AD 1500 – Feb AD 1600−1Mar AD 5100 – Feb AD 52000Mar AD 8700 – Feb AD 8800+1
Mar AD 1600 – Feb AD 28000Mar AD 5200 – Feb AD 6400+1Mar AD 8800 – Feb AD 10000+2
Mar AD 2800 – Feb AD 2900+1Mar AD 6400 – Feb AD 6500+2Mar AD 10000 – Feb AD 10100+3
Mar AD 2900 – Feb AD 32000Mar AD 6500 – Feb AD 6800+1Mar AD 10100 – Feb AD 10400+2
Mar AD 3200 – Feb AD 3300+1Mar AD 6800 – Feb AD 6900+2Mar AD 10400 – Feb AD 10500+3
Mar AD 3300 – Feb AD 36000Mar AD 6900 – Feb AD 7200+1Mar AD 10500 – Feb AD 10800+2

In 900 Julian years there are ​900⁄4 = 225 leap days. The Revised Julian leap rule omits seven of nine century leap years, leaving 225−7 = 218 leap days per 900-year cycle. Thus the calendar mean year is 365 + ​218⁄900 days, but this is actually a double-cycle that reduces to 365 + ​109⁄450 = 365.242 days, or exactly 365 days 5 hours 48 minutes 48 seconds, which is exactly 24 seconds shorter than the Gregorian mean year of 365.2425 days, so in the long term on average the Revised Julian calendar pulls ahead of the Gregorian calendar by one day in 3600 years.

The number of days per Revised Julian cycle = 900 × 365 + 218 = 328,718 days. Taking mod 7 leaves a remainder of 5, so like the Julian calendar, but unlike the Gregorian calendar, the Revised Julian calendar cycle does not contain a whole number of weeks. Therefore, a full repetition of the Revised Julian leap cycle with respect to the seven-day weekly cycle is seven times the cycle length = 7 × 900 = 6300 years.

Epoch

The epoch of the original Julian calendar was on the Saturday before the Monday that was the epoch of the Gregorian calendar. In other words, Gregorian 1 January 1 AD = Julian 3 January 1 AD.

However, the Revised Julian reform not only changed the leap rule but also made the epoch the same as that of the Gregorian calendar. This seems to have been carried out implicitly, and even scientific articles make no mention of it.[9]

Nevertheless, it is impossible to implement calendrical calculations and calendar date conversion software without appreciating this detail and taking the 2-day shift (with the original Julian calendar) into account. If the original Julian calendar epoch is mistakenly used in such calculations then there is no way to reproduce the currently accepted dating of the Revised Julian calendar, which yields no difference between Gregorian and Revised Julian dates from the 17th to the 28th centuries and most other centuries since the start of the Christian era (including the two first).

March equinox

The following is a scatter plot of actual astronomical northward equinox moments as numerically integrated by SOLEX 11[10][11] using DE421 mode[12] with extended (80-bit) floating point precision, high integration order (18th order), and forced solar mass loss[13] ("forced" means taken into account at all times). SOLEX can automatically search for northern hemisphere spring equinox moments by finding when the solar declination crosses the celestial equator northward, and then it outputs that data as the Terrestrial Time day and fraction of day relative to 1 January 2000 at noon (J2000.0 epoch). The progressive tidal slowing of the Earth rotation rate was accounted for by subtracting ΔT as calculated by the Espenak-Meeus polynomial set recommended at the NASA Eclipses web site[14] to obtain the J2000.0-relative Universal Time moments, which were then properly converted to Revised Julian dates and Jerusalem local apparent time, taking local apparent midnight as the beginning of each calendar day. The year range of the chart was limited to dates before the year AD 4400  -by then ΔT is expected to accumulate to about six hours, with an uncertainty of less than ​2 1⁄2 hours.[15]

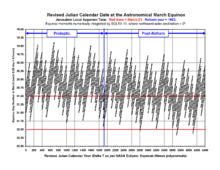
Equinox-Revised-Julian-Jerusalem-SOLEX-11

The chart shows that the long-term equinox drift of the Revised Julian calendar is quite satisfactory, at least until AD 4400 . The medium-term wobble spans about two days because, like the Gregorian calendar, the leap years of the Revised Julian calendar are not smoothly spread: they occur mostly at intervals of four years but there are occasional eight-year gaps (at 7 out of 9 century years). Evidently each of the authorities responsible for the Gregorian and Revised Julian calendars, respectively, accepted a modest amount of medium-term equinox wobble for the sake of traditionally perceived leap rule mental arithmetic simplicity. Therefore, the wobble is essentially a curiosity that is of no practical or ritual concern.

Adoption

The new calendar has been adopted by Orthodox churches as follows:

  • 1923: Estonia (accepted the Gregorian calendar, including the Gregorian Paschalion, but in 1945 joined the Moscow Patriarchate and reverted to Julian; after re-establishing in 1996, the Estonian Apostolic Orthodox Church adopted the Revised Julian calendar in 2012)
  • 1923: Finland (uses the Gregorian calendar, including the Gregorian Paschalion)
  • 10/23 March 1924: Constantinople, Cyprus and Greece
  • 1/14 October 1924: Poland (Very few parishes changed - on 2/15 June 2014 the Church switched back, but individual parishes may use the Revised Julian calendar if they wish)
  • 1/14 October 1924: Romania
  • 1/14 October 1928: Alexandria and Antioch
  • The Albanian Orthodox Church became autocephalous on 12 April 1937
  • 7/20 December 1968: Bulgaria [16]

Adopting churches are known as New calendarists. The new calendar has not been adopted by the Orthodox churches of Jerusalem, Russia, Serbia (including the uncanonical Macedonian Orthodox Church), Georgia, Ukraine (as well as the churches loyal to Moscow), Mount Athos and the Greek Old Calendarists. Although Milanković stated that the Russian Orthodox Church adopted the new calendar in 1923, the present church continues to use the Julian calendar for both its fixed festivals and for Easter. A solution to this conundrum is to hypothesize that it was accepted only by the short-lived schismatic Renovationist Church, which had seized church buildings with the support of the Soviet government while Patriarch Tikhon was under house arrest. After his release, on 15 July 1923, he declared that all Renovationist decrees were without grace, presumably including its acceptance of the new calendar.[17]

Defense

The basic justification for the new calendar is the known errors of the Julian calendar, which will in the course of time lead to a situation in which those following the Julian calendar (in the Northern Hemisphere) will be reckoning the month of December (and the feast of Christ's Nativity) during the heat of summer, August and its feasts during the deep cold of winter, Easter during the autumn season, and the November feasts in the springtime. This would conflict with the Church's historic practice of celebrating Christ's birth on 25 December, a date chosen for a number of reasons.[18] One of the reasons mentioned by Bennet is the time of the winter solstice, when the days begin to lengthen again as the physical sun makes its reappearance, along with the fact that Christ has traditionally been recognized by Christians as the metaphorical and spiritual sun who fulfills Malachi's prophetic words: "the sun of righteousness will shine with healing in its wings" (Malachi 4:2). The identification, based on this prophecy, of Jesus Christ as the "sun of righteousness" is found many times in writings of the early Church fathers[19] and follows from many New Testament references linking Jesus with imagery of sun and light.[19]

The defenders of the new calendar do not regard the Julian calendar as having any particular divine sanction (for more on this, see below); rather, they view the Julian calendar as a device of human technology, and thus subject to improvement or replacement just as many other devices of technology that were in use at the dawn of the Church have been replaced with newer forms of technology.

Supporters of the new calendar can also point to certain pastoral problems that are resolved by its adoption.

(1) Parishes observing the Julian calendar are faced with the problem that parishioners are supposed to continue fasting throughout western Christmas and New Year, seasons when their families and friends are likely to be feasting and celebrating New Year, often with parties, use of liquor, etc. This situation presents obvious temptations, which are eliminated when the new calendar is adopted.

(2) Another pastoral problem is the tendency of some local American media to focus attention each year on the 7 January (N.S.) / 25 December (O.S.) celebration of Christmas, even in localities where most Orthodox parishes follow the new calendar. So too, in all likelihood, do certain non-Orthodox churches profit from the Orthodox remaining Old Style, since the 7 January observance of Christmas among the Orthodox tends to focus attention on ethnic identifications of the feast, rather than on its Christian, dogmatic significance; which, in turn, tends to foster the impression in the public mind that for the Orthodox, the feast of Christ's Nativity is centered on the observance of the Julian date of that feast, rather than on the commemoration of Christ's birth. Such a focus appears to the defenders of the Revised Julian calendar and to many non-Orthodox as well, as a practice that is charming and quaint, but also anachronistic, unscientific and hence ultimately unreasonable and even cultish.

(3) Some Orthodox themselves may unwittingly reinforce this impression by ignorance of their own faith and by a consequential exclusive, or excessive, focus on the calendar issue: it has been observed, anecdotally, that some Russians cannot cite any difference in belief or practice between their faith and the faith of western Christians, except for the 13-day calendar difference.

Against the new calendar, the argument is made that inasmuch as the use of the Julian calendar was implicit in the decision of the First Ecumenical Council at Nicaea (325), no authority less than an Ecumenical Council may change this decision. However, the fact is that that Council made no decision or decree at all concerning the Julian calendar. Its silence constituted an implicit acceptance not of the Julian calendar, but of the civil calendar, which happened to be, at that time, the Julian calendar (the explicit decision of Nicaea being concerned, rather, with the date of Easter). By virtue of this, defenders of the new calendar argue that no decision by an Ecumenical Council was or is necessary today in order to revise (not abandon) the Julian calendar; and further, that by making the revision, the Church stays with the spirit of Nicaea I by keeping with the civil calendar in all its essentials—while conversely, failure to keep with the civil calendar could be seen as a departure from the spirit of Nicaea I in this respect. Lastly, it is argued that since the adoption of the new calendar evidently involves no change in or departure from the theological or the ethical teachings of Orthodox Christianity, but rather amounts to a merely disciplinary or administrative change—a clock correction of sorts—the authority to enact that change falls within the competency of contemporary, local episcopal authority. Implicit acceptance of this line of reasoning, or something very close to it, underlies the decision to adopt the new calendar by those Orthodox churches that have done so.

It follows that, in general, the defenders of the new calendar hold the view that in localities where the Church's episcopal authority has elected to adopt the new calendar, but where some have broken communion with those implementing this change, it is those who have broken communion who have in fact introduced the disunity, rather than the new calendar itself or those who have adopted it — although most would agree that attempts at various times to mandate the use of the new calendar through compulsion, have magnified the disunity.

To the objection that the new calendar has created problems by adjusting only the fixed calendar, while leaving all of the commemorations in the moveable cycle on the original Julian calendar, the obvious answer, of course, is that the 1923 Synod, which adopted the new calendar, did in fact change the moveable calendar as well, and that calendar problems introduced as a result of the adoption of the (fixed) new calendar alone, would not have existed had the corrections to the moveable calendar also been implemented.

According to the defenders of the new calendar, the argument that the 25 December (N.S.) observance of Christmas is a purely secular observance and is therefore an unsuitable time for Orthodox Christians to celebrate Christ's Nativity, is plainly inaccurate, since the 25 December observances of Christ's birth among western Christians (and today, among many Orthodox Christians) obviously occur overwhelmingly in places of worship and involve hymns, prayers, scripture readings, religious dramas, liturgical concerts, and the like. Defenders of the new calendar further note that, to the extent that 25 December is a secular observance in the western world, 7 January (i.e., 25 December O.S.) appears to be becoming one as well, in Orthodox countries that continue to follow the old calendar. In Russia, for example, 7 January is no longer a spiritual holiday for Orthodox Christians alone, but has now become a national (hence secular) holiday for all Russians, including non-Orthodox Christians, people of other religions, and nonbelievers. Where this will lead in the end remains to be seen.

Among other arguments by defenders of the new calendar are those made on the basis of truth (notwithstanding that the detractors of that calendar make the claim that the Old Style date, 7 January / 25 December, is the true celebration of Christ's Nativity). Arguments from truth can take two forms: (1) If a calendar is a system for reckoning time based on the motions of astronomical bodies—specifically the movements of Sun and Moon, in the case of the church calendar—and if precision or accuracy is understood as one aspect of truth, then a calendar that is more accurate and precise with respect to the motions of those bodies must be regarded as truer than one that is less precise. In this regard, some of those who champion the old calendar as truth (rather than for pastoral reasons, as seems to be the case with the national churches that adhere to it) may appear, to those following the new calendar, as the defenders of a fiction. (2) Some defenders of the new calendar argue that the celebration, in any way or form, of two feasts of Christ's Nativity within the same liturgical year is not possible, since according to the faith there is only one celebration of that feast in a given year. On this basis, they argue that those who prefer to observe a "secular" feast of the Nativity on 25 December and a "religious" one on 7 January, err in respect of the truth that there is but one feast of the Nativity each year.

Criticism

While the new calendar has been adopted by many of the smaller national churches, a majority of Orthodox Christians continue to adhere to the traditional Julian calendar, and there has been much acrimony between the two parties over the decades since the change, leading sometimes even to violence, especially in Greece.

Critics see the change in calendar as an unwarranted innovation, influenced by Western society. They say that no sound theological reason has been given for changing the calendar, that the only reasons advanced are social. The proposal for change was introduced by Meletios Metaxakis, Ecumenical Patriarch of Constantinople, a patriarch whose canonical status has been disputed.[20]

The argument is also made that since the use of the Julian calendar was implicit in the decision of the First Ecumenical Council at Nicaea (325), which standardized the calculation of the date of Easter, no authority less than an Ecumenical Council may change it. It is further argued that the adoption of the new calendar in some countries and not in others has broken the liturgical unity of the Eastern Orthodox churches, undoing the decision made by the council of bishops at Nicaea to decree that all local churches celebrate Easter on the same day. The emperor Constantine, writing to the bishops absent from the Council to notify them of the decision, argued, "Think, then, how unseemly it is, that on the same day some should be fasting whilst others are seated at a banquet".[21]

Liturgical objections to the new calendar stem from the fact that it adjusts only those liturgical celebrations that occur on fixed calendar dates, leaving all of the commemorations on the moveable cycle on the original Julian calendar. This upsets the harmony and balance of the liturgical year. (This would not have been a problem if the recommendations of the 1923 synod to use an astronomical rule to reckon the date of Easter, as outlined above, had not been rejected.) This disruption is most noticeable during Great Lent. Certain feast days are designed to fall during Lent, such as the feast of the Forty Martyrs of Sebaste. The Feast of the Annunciation is also intended to fall either before Easter or during Bright Week. Sometimes, Annunciation will fall on the day of Easter itself, a very special concurrence known as Kyrio-Pascha, with special liturgical practices appointed for such an occurrence. However, under the new calendar, Kyrio-Pascha becomes an impossibility. The Apostles' Fast displays the most difficult aspect of the new calendar. The fast begins on the moveable cycle and ends on the fixed date of 29 June; since the new calendar is 13 days ahead of the traditional Julian calendar, the Apostles' Fast is 13 days shorter for those who follow the new calendar, and some years it is completely abrogated. Furthermore, critics of the new calendar point out the advantage to celebrating Nativity separately from the secular observances of Christmas and New Year, which are associated with partying and alcohol consumption.

Critics also point out that proponents of the new calendar tend to use worldly rather than spiritual justification for changing the calendar: wanting to "party with everyone else" at Christmas; concern that the gradual shift in the Julian calendar will somehow negatively affect the celebration of feasts that are linked to the seasons of the year. However, opponents counter that the seasons are reversed in the southern hemisphere, where the liturgical celebrations are no less valid. The validity of this argument is questionable, since the feasts of the Orthodox Church were not changed no matter where they were celebrated, and Orthodox services were held in the southern hemisphere with little issue centuries before the introduction of the new calendar.

Proponents also argue that the new calendar is somehow more "scientific", but opponents argue that science is not the primary concern of the Church; rather, the Church is concerned with other-worldliness, with being "in the world, but not of it", fixing the attention of the faithful on eternity. Scientifically speaking, neither the Gregorian calendar nor the new calendar is absolutely precise. This is because the solar year cannot be evenly divided into 24-hour segments. So any public calendar is imprecise; it is simply an agreed-upon designation of days.

From a spiritual perspective, Old Calendarists also point to a number of miraculous occurrences that occur on the old calendar exclusively, such as the "descent of the cloud on the mount" on the feast of the Transfiguration. After the calendar change was instituted, the followers of the old calendar in Greece apparently witnessed the appearance of a cross in the sky, visible to thousands on the feast of the Exaltation of the Holy Cross, 1925, of which eyewitness accounts were recorded.[22]

For such special events, if the original Julian date and year is known then the option always exists to calculate what was the proleptic Revised Julian date of that event and then observe its anniversary on that day, if that could be socially and ritually accepted.

Revised Julian calendrical calculations

The calendrical arithmetic discussed here is adapted from Gregorian and Julian calendar arithmetic published by Dershowitz and Reingold, although those authors explicitly ignored the Revised Julian calendar.[23] Their book, referred to hereinafter as CC3, should be consulted for methods to handle BC dates and the traditional omission of a year zero, both of which are ignored here. They define the MOD operator as x MOD y = x − y × floor(x / y), because that expression is valid for negative and floating point operands, returning the remainder from dividing x by y while discarding the quotient.[24] Expressions like floor(x / y) return the quotient from dividing x by y while discarding the remainder.

Leap rule

isLeapYear = (year MOD 4 = 0)

IF isLeapYear THEN

IF year MOD 100 = 0 THEN
Century = (year / 100) MOD 9
isLeapYear = (Century=2) OR (Century=6)
END IF

END IF

Fixed days

Calendrical calculations are made consistent and straightforward for arithmetic operations if dates are first converted to an ordinal number of days relative to an agreed-upon epoch, in this case the Revised Julian epoch, which was the same as the Gregorian epoch. To find the difference between any two Revised Julian dates, convert both to ordinal day counts and simply subtract. To find a past or future date, convert a given date to an ordinal day count, subtract or add the desired number of days, then convert the result to a Revised Julian date.

The arithmetic given here will not "crash" if an invalid date is given. To verify that a given date is a valid Revised Julian date, convert it to an ordinal day count and then back to a Revised Julian date—if the final date differs from the given date then the given date is invalid. This method should also be used to validate any implementation of calendrical arithmetic, by iteratively checking thousands of random and sequential dates for such errors.

To convert a Revised Julian date to any other calendar, first convert it to an ordinal day count, and then all that is needed is a function to convert the ordinal days count to that calendar. To convert a date from any other calendar to a Revised Julian date, first convert that calendar date to an ordinal day count, then convert ordinal days to the Revised Julian date.

The following constant defined midnight at the start of Revised Julian date Monday, 1 January 1 AD as the beginning of the first ordinal day. This moment was Julian day number 1721425.5.

RJepoch = 1

CC3 outlines functions for Gregorian and Julian calendar conversions,[25] as well as many other calendars, always calculating in terms of the ordinal day number, which they call the "fixed date" or rata die (RD), assigning the number 1 to the Gregorian calendar epoch. The arithmetic herein, by using the same ordinal day numbering epoch, is fully compatible with all CC3 functions for calendrical calculations and date inter-conversions.

One can assign a different integer to the Revised Julian epoch, for the purpose of numbering ordinal days relative to some other epoch, but if you do so then one must take the epoch difference into account when using any CC3 calendar functions and when converting an ordinal day number to a weekday number.

Optionally the ordinal day number can include a fractional component to represent the time as the elapsed fraction of a day. The ordinal day number of the J2000 moment (1 January 2000 noon) was 730120.5.

Revised Julian to fixed days

Convert a year, month, and day to the corresponding fixed day number:

PriorYear = year − 1
FixedDays = RJepoch + 365 × PriorYear + floor(PriorYear / 4) + floor((367 × month − 362) / 12) + day − 1

If month is after February then subtract 1 day for a leap year or subtract 2 days for a common year:

IF month > 2 THEN
IF isLeapYear(year) THEN
FixedDays = FixedDays − 1
ELSE
FixedDays = FixedDays − 2
END IF
END IF

Finally subtract a day for each prior century year (most of which are non-leap) and then add back in the number of prior century leap years:

PriorCenturies = floor(PriorYear / 100)
FixedDays = FixedDays − PriorCenturies + floor((2 × PriorCenturies + 6) / 9)

Fixed days to Revised Julian

Convert an ordinal day number to the corresponding Revised Julian year, month, and day, starting by removing any fractional time-of-day portion:

Days = floor(FixedDays) − RJepoch + 1
PriorCenturies = floor(Days / 36524)
RemainingDays = Days − 36524 × PriorCenturies - floor((2 × PriorCenturies + 6) / 9)
PriorSubcycles = floor(RemainingDays / 1461)
RemainingDays = RemainingDays MOD 1461
PriorSubcycleYears = floor(RemainingDays / 365)
year = 100 × PriorCenturies + 4 × PriorSubcycles + PriorSubcycleYears
RemainingDays = RemainingDays MOD 365
IF RemainingDays = 0 THEN
This is either the 365th day of a common year, or the 365th or 366th day of a leap year. Either way, we have to decrement the year because we went one year too far:
year = year − 1
IF isLeapYear(year) AND PriorSubcycles=0 THEN RemainingDays=366 ELSE RemainingDays=365
END IF
PriorDays = RemainingDays − 1
IF isLeapYear(year) THEN correction = 1 ELSE correction = 0
IF PriorDays < (31+28+correction) THEN correction = 0 ELSE correction = 2 − correction
Month = floor((12 × (PriorDays + correction) + 373) / 367)

Finally, calculate the day number within the month by subtracting the Fixed days count for the start of the month from the originally given Fixed days count, and then add one day:

Day = FixedDays - RevisedJulianToFixed(year, month, 1) + 1

Fixed days to weekday number

Convert the ordinal number of days since the Revised Julian epoch to a weekday number (Sunday=1 through Saturday = 7):

WeekdayNumber = (floor(FixedDays) − RJepoch + 1) MOD 7 + 1

Don't be tempted to omit subtracting the RJepoch just because it is offset by adding +1. As written, this expression is robust even if you assign a value other than one to the epoch.

Notes
  1. "Gregorian Calendar". Encyclopædia Britannica. Retrieved 20 April 2010.
  2. "The Revised Julian Calendar". Time and Date. Retrieved 25 December 2017.
  3. The Orthodox Church Calendar. 1996. p. 27. ISBN 9780884650621. The Church of Greece accepted the New Calendar on March 1, 1924. Archbishop Chrysostomos (Papadopoulos) of Athens must have forgotten the words he wrote while still an Archimandrite in a report given to the Greek government by the five member commission on the question of calendar reform in January, 1923: …
  4. Maksim Trpković, Reforma kalendara, Belgrade 1900.
  5. Cassian, Hieromonk (1998). A Scientific Examination of the Orthodox Church Calendar. Center for Traditionalist Orthodox Studies. pp. 51–52. ISBN 978-0-911165-31-9.
  6. The Romanian church adopted the new calendar on the date specified by the conference. As the Julian Easter continued to be observed, in 1926 it would have fallen outside the canonical limits. The church decreed that the Gregorian Easter would be observed instead, which led to dissent. The same thing happened in 1929. This time there was civil disorder and churches were barricaded. The experiment was not repeated.
  7. Milankovitch, M. (1924). "Das Ende des julianischen Kalenders und der neue Kalender der orientalischen Kirchen". Astronomische Nachrichten (in German). 220 (5279): 379–384. Bibcode:1924AN....220..379M. doi:10.1002/asna.19232202303.
  8. Shields, Miriam Nancy (1924). "The new calendar of the Eastern churches". Popular Astronomy. 32: 407–411. Bibcode:1924PA.....32..407S. This is a translation of the paper by Milankovitch in Astronomische Nachrichten.
  9. Dimitrijević, M.S. & Theodossiou, E. (2002). "The calendar of the Greek Orthodox Church" (PDF). Astronomical & Astrophysical Transactions. 21 (1): 145–147. Bibcode:2002A&AT...21..145D. doi:10.1080/10556790215577.
  10. Vitagliano, Aldo (1997). "Numerical integration for the real time production of fundamental ephemerides over a wide time span" (PDF). Celestial Mechanics and Dynamical Astronomy. 66 (3): 293–308. Bibcode:1996CeMDA..66..293V. doi:10.1007/bf00049383. Archived from the original (PDF) on 22 July 2011.
  11. "The SOLEX home page". Archived from the original on 3 April 2011.
  12. Folkner, W. M.; Williams, J. G. & Boggs, D. H. (31 March 2008). "The Planetary and Lunar Ephemeris DE 421" (PDF). Jet Propulsion Laboratory, California Institute of Technology, Memorandum. IOM 343R-08-003. Archived from the original (PDF) on 2 May 2013.
  13. Noerdlinger, Peter D. (2008). "Solar Mass Loss, the Astronomical Unit, and the Scale of the Solar System". arXiv:0801.3807 [astro-ph].
  14. "Eclipses Delta T web site". NASA. Gives the Espenak-Meeus polynomial expressions for Delta T.
  15. "Uncertainty in Delta T (ΔT)".
  16. Clogg 2002, pp. 8–9.
  17. Koestel 2012, p. 157.
  18. Bennett, David. "Choosing the Date of Christmas: Why is Christmas Celebrated on December 25?".
  19. Murdock, D.M.; Acharya S. "Jesus as the Sun Throughout History".
  20. The Orthodox Church Calendar: In Defense of the Julian Calendar. Jordanville, NY: Holy Trinity Monastery. 1996. p. 11. ISBN 978-0884650621.
  21. Eusebius. "On the Keeping of Easter". Vita Const. Lib. iii., 18–20. Retrieved 4 June 2007.
  22. "The Appearance of the Sign of the Cross Near Athens in 1925".
  23. Dershowitz, Nachum; Reingold, Edward M. (2008). Calendrical Calculations (3rd ed.). Cambridge University Press. p. 47, footnote 3. Archived from the original on 12 July 2008.
  24. Dershowitz, Nachum; Reingold, Edward M. (2008). Calendrical Calculations (3rd ed.). Cambridge University Press. p. 18, equation 1.15. Archived from the original on 12 July 2008.
  25. For example, see "alt-fixed-from-gregorian" in Dershowitz, Nachum; Reingold, Edward M. "Errata" (PDF). Calendrical Calculations: The Millennium Edition (2nd ed.). Cambridge University Press. erratum 106, equation 2.25.
gollark: Really? Hmm.
gollark: Because of its approach to drivers, actually, it's *not* always.
gollark: It's more compatible with *some* things.
gollark: They have never mentioned anything like "I need to run this Windows-only software".
gollark: Well, somewhat better, sure, but that's... not relevant?

References
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.