Lifeline Volume 3
| Lifeline Volume 3 | ||
| ||
| Published in | September 1971 | |
|---|---|---|
| Preceded by | Volume 2 | |
| Succeeded by | Volume 4 | |
| This page is a transcript of Volume 3 of the Lifeline newsletter |
|---|
| This article may contain spelling mistakes and/or errors that will not be corrected -- it is preserved in this way for history's sake |
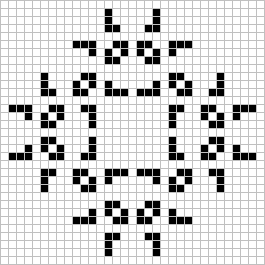
A QUARTERLY NEWSLETTER FOR ENTHUSIASTS OF JOHN CONWAY'S GAME OF LIFE O OOOOO OOOOO OOOOO O OOOOO O O OOOOO O O O O O O OO O O O O OOO OOO O O O O O OOO O O O O O O O OO O OOOOO OOOOO O OOOOO OOOOO OOOOO O O OOOOO Number 3 SEPTEMBER 1971• Editor and Publisher - Robert T. Wainwright •
Page 1
New inquiries to LIFELINE are still coming in but (fortunately) the rate is decreasing. With the readership base almost established at more than 500, I can afford to devote more attention to the many new developments which are occurring at a rate very nearly proportional to time (since October 1970) squared. In order to maintain some degree of continuity in these series of newsletters, I will continue to follow the general outline of previous issues. While doing so I will point out new and the more interesting developments as well as answer (and pose) some new questions about this incredible game.

When I first outlined this issue in late August, it appeared that well over two-thirds of the new developments were in the area of Life dealing with transfinite objects. In early September, I recived some information from the group at the M.I.T. Artificial Intelligence Laboratory (Gosper, et.al.) which convinced me there are still many surprises in the finite kingdom of Life. After reading this issue, I am sure you will agree that LIFELINE Number THree will very likely be remembered for the extraordinary achievements reported.
In this issue I will cover first, the area of Life dealing with finite objects and events, then activity associated with one-dimensionally infinite objects ('wicks') which includes fuses, next activity associated with two-dimensionally infinite objects (agars), and finally developments in other selected areas of cellular automina.
The expanded classification system for finite Life objects makes it more convenient to identify and place new discoveries. However, Class V which includes Life events needs some further refinement. I will go thru each subclass in turn discussing new developments. These are definitely not in any order of significance.
Page 2
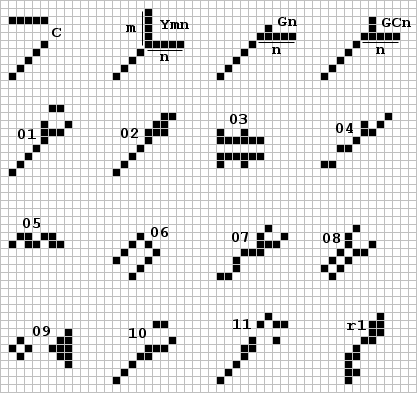
I am compiling a catalogue of all Class I objects (still lifes) of fourteen or less bits. As a start, I would be interested to see if you have any objects n ≤ 9 besides those shown below. Objects previously mentioned in either Scientific American or LIFELINE are given by their name while the new ones (each of which were sent in by several readers) are referred to only by size. Regarding cataloging of this class, Lee H. Skinner of Albuquerque, N. Mexico has elaborately recorded in color over 300 such objects including those shown below. The M.I.T. group have discovered some very unusual properties of the fishhook (No.2,p.3). This nonsymmetrical still life which they call the 'eater' will be discussed in several other parts of this issue.
| Size | The smallest still life objects showing families of similar structure |
Sum | ||||||
|---|---|---|---|---|---|---|---|---|
| ≤ 3 | none | |||||||
| 4 | block | tub | 2 | |||||
| 5 | boat | 1 | ||||||
| 6 | ship | barge | snake | beehive | aircraft carrier | 5 | ||
| 7 | long boat | (7.1) | loaf | fishhook (eater) | 4 | |||
| 8 | long ship | long barge | (8.1) | (8.2) | pond, (8.3) | tub w/tail, shillelagh, (8.4) | 9 | |
| 9 | (9.1) | (9.2) | (9.3) | hat, (9.4), (9.5), (9.6) | 7 | |||
| 4+2i | 4+2i | 5+2i | 6+i | 8+i | i = 0,1,2,... | |||
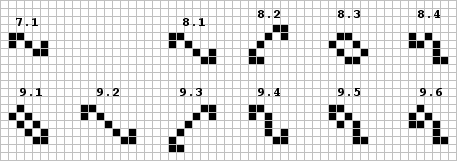 The remaining unpublished smallest still lifes | ||||||||
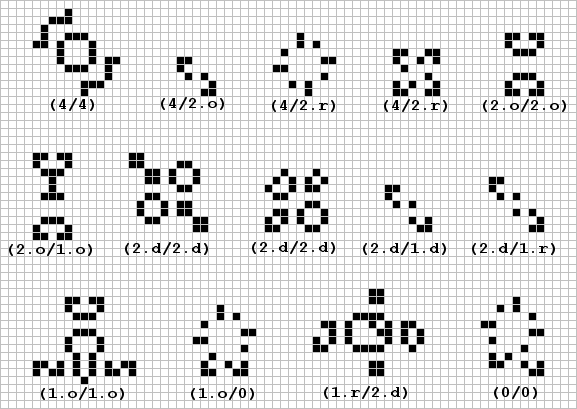
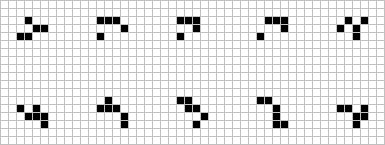
Class II.A (all period two oscillators) is sufficiently large and common to be further divided into subgroups by symmetry of the active area (not the entire object). Rather than choosing the smallest object in each group or explaining what active area symmetry means (i.e. cells in both phases or one phase), I have chosen the more unusual examples to illustrate the variety of this subclass. Because so many readers reported one or more of these figures, I will show only the object with a descriptive name without reference to the inventor.
Page 3
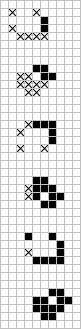
Left to right: scrubber, bipole, flip-flops, quad, spark coil
piston, semifore, still? lifes?, tripole, quadpole
light bulb, almosymmetric, negentropy, asymmetric

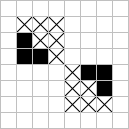
Class II.B (billiard table configurations) has several new additions, the most noteworthy of these being the period eight object shown to the left discovered independently by Don Woods of Natick, Mass. and the writer. You can pick either of the two names (both eight letters) which adequately describe the internal activity of this now empty oscillator. The inductor coils shown here have been modified slightly from each original. The M.I.T. group have reported a similar object with a slight difference in one end of the table (the lid?). By reforming the nine-bit lid they developed the period three 'pressure cooker' (my term) shown to the right. Placing these two objects end-to-end (without the inductor coils) results in a single object of period 24. The hustler (No.2,p.3) can likewise use latent blocks (![]()
So many readers wrote asking why the oscillator discovered by Rich Schroeppel of the M.I.T. groups (No.1,p.5) was not in Class II.B that I decided it really belongs here even though its table is not enclosed. The period three 'double ewe' developed by the writer is presented in this class for the same reason. A modified beacon is used to prevent overloading of the two stable diagonal bit pairs (shown as solid dots).
Page 4
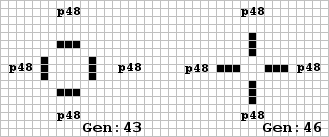
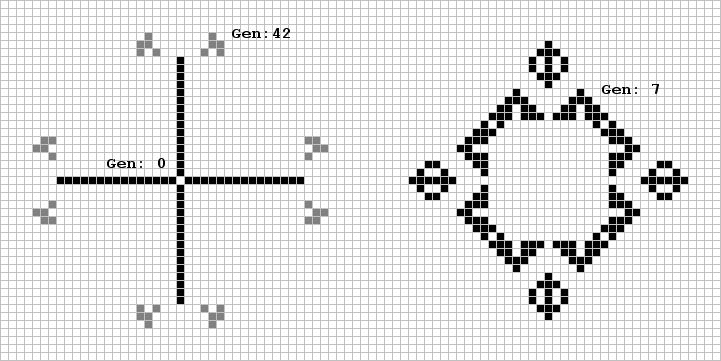
Class II.C objects (inductors) are less common but by an alternate placing of the pulsar quadrants, you can construct any number of larger period three forms. I coined 'quasar' for the new Class II.C object shown below. Earl C. Abbe of McLean, Va. reports his discovery of a period six arrangement which in 43 generations evolves from the order ten hollow diamond (with extended sides). A schematic of the first and fourth phases are shown here.
Class II.D objects (pulsators) are very uncommon and now have the period eight object shown here discovered by Jan Kok of the M.I.T. group. If you track this object, you will note the last period creates four sparks.
Class II.E (shuttles) now contains the 'twin bees' of an unusual period 46! A mirror pair of the now familiar B-heptominoes are used as the super shuttle in this oscillator shown at the left below. Descovered by R. William Gosper, Jr. of the M.I.T. group, this object plays a key role in other constructions to be discussed later in this newsletter.

Page 5
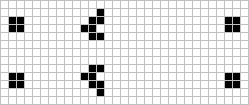
Note there are now three types of shuttle element known. The 'gourmet bee and eater' shown to the right (above) like its cousin, the hungry bee (No.2,p.4), requires subsistence every thirty generations in order to survive. In this case however, a pentadecathlon (the 'chef') is needed to first prepare a block from the glider. Also shown is the eater about to enjoy one of its many different types of prey, a latent beehive. The eater will consume a pre-latent beehive from a not yet mature queen bee thereby allowing the compact period thirty shuttle shown at the right to operate. The eater can also be used in several ways to maintain the period 46 super shuttle (not shown).

If two eaters are placed together, they do not destroy each other but rather form a period three oscillator! Presented here in Class II.F (miscellaneous), this objct is probably the smallest (P3).

Again, I must report that no new basic spaceships (Class III) were reported. However, much more will be said about some new special spaceship flotillae in Class IV.B. Additionally, an entire family of true one-dimensionally infinite spaceships (moving wicks) has been reported and will be discussed later. A way of escorting an overweight spaceship which is two units longer (14 versus the 12 given in the Nov.col, p.118) by two heavyweight ones was reported by Abbe and is shown to the right above.
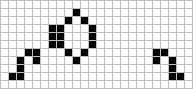
Class IV unquestionably ranks as the highlight of this issue including a basically new type of glider gun (Class IV.A)! More significantly, several basic puffer trains (Class IV.B) have been discovered including two that create gliders!! These discoveries made by the group at the Artificial Intelligence Laboratory at M.I.T. (R. William Gosper, Jr., Rici Liknaitzky, Bill Mann, and Michael Speciner) have significance in the theory of turing machines and universal constructors which will be discussed in the later part of this newsletter. Using two of the twin bees, Gosper succeeded in finding the precise timing and positioning (at right angles) that would, every 46 generations, create a glider! This 'Newgun' (Class IV.A) is shown here.
Page 6
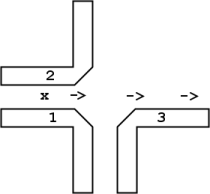
The spaceship factory mentioned by Martin Gardner in the February column was never presented mainly due to its large size and long period. It consisted of a complex arrangement of position and timing of eight Guns which created a middleweight spaceship about every 300 generations. More recently, Gosper succeeded in reducing this to a period 60 factory using four Guns and one pentadecathlon (a slight change in timing of two of the Guns allowed the factory to produce lightweight spaceships instead). The writer has positioned three Newguns to generate a middleweight spaceship every 46 generations. A schematic of this last arrangement and the productive mechanism are shown to the right. The proximity of the third glider to the escaping spaceship prevents this from being done with period 30 Guns.

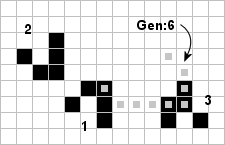
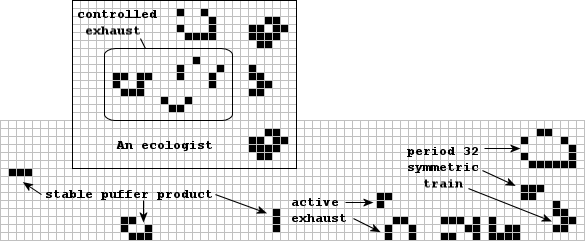
By placing various combinations of the B-heptomino (including the super shuttle) amongst various spaceship flottilae, Gosper has discovered a number of configurations that travel at .5C with periods of multiple 20 or 32 leaving behind various types of exhaust!! The simplest of these, 'Puffer Train' (the mere yet incredible 22 bit object to the left) has two lightweight spaceships escorting an engine which flips over every ten generations, tending to make period 20 (special period 10) residue. The new residue is very vigorous, however, and reacts violently with older residue along the path. After an initial transient which interestingly takes 1971 generations, the Puffer Train develops a special period of 70 with glide reflection symmetry, but the flame of instability is nearly 1,000 cells long! Catalysis by a third lightweight spaceship completely inhibits the exhaust (see the 'ecologist' below). The further addition of a fourth lightweight spaceship creates a spark which rekindles the dying residue every 20 generation, producing the 'Space Rake' (next page) with a dense forward wave (not a stream) of gliders five diagonal cells apart.
Another variety of puffer train is symmetrical, leaving (temporal) period 64 blocks and period 32 rearward gliders, either of which can be inhibited by additional spaceships. Not shown here, the 'Glider Train' will be referred to later in discussing some other, more complex constructions. A somewhat less spectacular cousin of this last train is the period 32 symmetric train which every 128 generations creates two pairs of blinkers and one pair of 'bookends' (Gosper's term). One mirror half of this train is shown on the bottom of page six.
Page 7
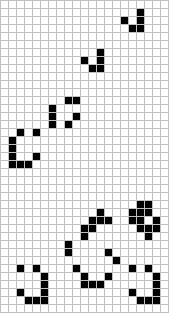
The fastest growth possible in a two dimensional cellular automaton (Life) is as a quadratic function of age, since any finite form will stay inside a circumscribed square which expands at the speed of light in all four directions. Speciner of the M.I.T. group designed and attempted to construct and test such a quadratic device. It consisted of two groups of twelve Glider Trains receding from each other along the X axis, launching period 128 rearward gliders which assembled Guns on the Y axis every 384 generations. Unfortunately, the population exceeded 21,000 bits before it completed its first Gun! Also, additional Glider Trains may have been needed to build eaters to inhibit Gun outputs from provoking Train debris which would counterattack the Guns.
The M.I.T. group challenge the readers to determine the speed at which a wave of collisions will propagate up the Y axis given the sources are receding at .5C along the X axis. I will publish their answer as well as other relevant correspondence received in issue Number Four.
The photograph on the cover page of LIFELINE Number Three shows the 'BREEDER' (my term), an advanced quadratic model, using only ten Trains (moving east) with exhaust precisely controlled to generate Guns along the X axis! Most of the Trains leave blocks (needed to delete every other glider from the next passing Train), since period 32 gliders would assemble the Guns too close together. The resolution of the photograph shows only dots for gliders, roughly a thousand of which are filling the triangular region on the left. Since at this moment (generation 3,333) thirty Guns are active, the growth rate is one glider per generations. This rate will, of course, increase steadilly without limit!! At about generation 6,500 the number of gliders in the field begins to surpass the BREEDER'S age. The BREEDER was run on a PDP-6 with only 16K of memory taking about two seconds per generation using a program written by Mann!
Regarding Class V objects in general, I would like to make known the industrious efforts of High W. Thompson of Lefrak City, N.Y. Thompson has single handedly developed a major 'Codex' system for recording data regarding Life objects and events (i.e. primarily Class V objects and their census). This is a kind of super LIFEFILE of 'lifebrary' of information. Without going into the details of his system of indexing, I want to mention and highlight what he has done because I think it represents the most significant attempt to record and keep track of this information. Thompson has agreed to include all information the readers want to send in and, to those interested, will be the source of raw data. Since Thompson records his information in a medium readily convertible to computer input form, it would be relatively easy to write a program to produce a set of reports displaying this information.
Page 8
For any Class V object stabilizing in less than 50 generations, he records each generation. For 'methuselahs' (a term coined by Thompson for any relatively small object with a life ≤ 50 generations), he records the first 20 generations and a picture of the final pattern (with age and census data). This is the minimum information he would like for any objects not listed in the LIFEFILE this issue. If you have data to be included in the codex, send it to the LIFELINE address along with your request for information in your special area of interest.
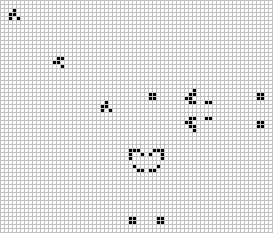
You might be interested in knowing there are 55 different possible transitions from a low to a higher order of symmetry given the eight states in Class I (actually only four levels - see No.2,p.2). Regarding Class V objects in general, it would be an interesting exercise to identify specific examples of all transitions. For instance, the first example shown here provided by Tad Marshall of Irvington, N.Y. is a minimum predecessor (six-bit) to the honeyfarm and illustrates order zero -> order one (rotational) -> order two (orthogonal) -> order four. The second example was sent in by J. Ubbink of Waalre, The Netherlands and illustrates a different path between the lowest and highest orders of symmetry (also the honeyfarm). Of course, once a path is known, all combinations within the path are also known.
Before discussing specific Class V objects, I would now like to introduce another interesting measure for these objects, also a ratio. Let's call F.I.P. the ratio of final to initial population for an object of Class V. The maximum value of this ratio is 1.33 for all three-bit objects, 3.00 for all four-bit objects, and 23.20 for all five-bit objects. If anyone reports an unusually high value for any larger objects, I will present their results in the next issue. Of course, for objects larger than 21 bits the maximum value is infinite.
Page 9

Class V.B includes the N-shaped object shown on the next page and sent in by Harvey Lerman of Maitland, Fla. After 20 generations it evolves into two B-heptominoes facing away from each other which by generation 113 have created two gliders each. The four gliders finally collide leaving in generation 176 a total census of six blocks and two ships. With two exceptions, Denis M. Wilson of Aberdeen, Scotland has tracked the family of crosses (both orthogonal and diagonal) up to 31 by 31. Robert Bison of Hopewell Jct., N.Y. successfully ran the two diagonal crosses to be discussed here which were not included in Wilson's study. The order fifteen (31 by 31) diagonal cross after 212 generations has evolved into a 'constellation' made up of a long barge separating the quadrants (N,E,S,W) each of which contains 4 blocks and 2 boats for a total population of 136 bits.


Class V.C includes the order eleven diagonal cross which after 245 generations has bookends separating the quadrants (NE,SE,SW,NW) each of which contains 6 blocks, 2 blinkers, and 2 traffic lights for a total population of 272 bits. Generation 243 includes the object shown at the far right which is amazingly similar to Collins' tumbler (Feb.col,p.115). This evolves into the bookends in tow generations. Thompson reports the eight-bit object shown here which in 22 generations becomes the 'interchange' (his term) which is similar to two traffic lights side-by-side with the adjacent blinkers removed. Shown below is the order ten hollow diamond with extended sides sent in by Abbe which yields the period six oscillator mentioned on page four.

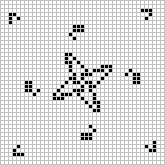
Class V.D.1 includes the 'nova' sent in by Wilson and shown here in a form slightly altered by the writer from the original. As Wilson says 'it explodes, throwing off four gliders, then suffers gravitational collapse when in generation 32 four other gliders are collapsing inward and later experiences a curious reversal of spiral twist during generations 108-114' (see next page). Finally in generation 127 the original four gliders head for the four corners of the universe leaving a skewed traffic light behind. This is a good example of a Class V object preserving order two (rotational) symmetry during a fairly long history. Interestingly, generation one of this object is an arrangement of four W pentominoes. Roger H. Rosenbaum of Seattle, Wash. sent in the 20 bit object at the right which after 177 generations creates 12 gliders and 'other residue' including 4 blocks, 4 beehives, and 8 blinkers making it the most prolific Class V glider generator (0.6 gliders per bit).
Page 10

Class V.D.2 (pure glider generators) includes the order fifteen orthogonal cross with the center bit removed which evolves into four pure glider generating objects each creating two gliders. First reported by Rosenbaum, the initial and final (generation 42) patterns supplied by Wilson are shown on the next page. Generation seven (shown) illustrates the beautiful symmetry displayed by this object. Interestingly, generation 19 is an arrangement of four underlined seven-bit W's.


The two other Class V.D.2 heptominoes are shown here along with all the five-bit glider predecessors known to the writer. Thee are at least 60 six-bit predecessors including the five kingwise connected ones shown below. Thompson who first identified the two heptominoes also sent in the six-bit predecessors and feels there are well over 100 of these. Interestingly, the ratio of beta glides to alpha gliders formed (see No.1,p.7) is exactly equal to four for both size predecessors.
The ten-bit object shown to the right above is a great-grandfather to the middleweight spaceship. By adding an additional bit (x) the object gives rise (also in the third generation) to a lightweight spaceship. These are involved in the productive mechanisms of the smaller spaceship factories mentioned earlier.
Page 11
Page 12

The top of page twelve shows spaceship factories mentioned earlier. Shown below are some more symmetric and n-omino type pure glider generators. Rosenbaum sent in the symmetric object which creates two gliders in only one generation. Abbe found the first omino shown here which in one generation becomes one glider. Wilson who reported the last three ominoes (including another undecomino!) points out an error in LIFELINE Number Two. The third undecomino on page five becomes three blocks and one blinker after a considerable time. It needs its mirror companion in order to become a glider.
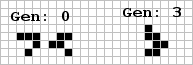
The puffer trains described on page six should be relatively easy to make with gliders. We have already discussed factories that produce lightweight and middleweight spaceship using glider streams. Shown to the right is a glider collision that creates the remaining component, the engine (a B-heptomino) in only three generations.
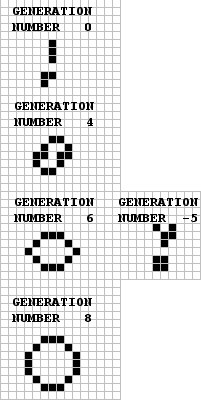
The acorn (Class V.F) introduced last issue is a seven-bit object discovered by Charles L. Corderman of Winchester, Mass. The data for this object which lives for an incredible 5,209 generations (!) is given in the table below. During its life history many gliders are created of which 13 manage to escape. Anyone attempting to track it may notice the activity appears to almost stop, then a glider is released which soon crashes into something and gets things going again. The fantastic printout of the final census ('oak tree') was supplied by Bison who verified the original results for the writer before issue Number Two was published. Woods was the only reader to successfully confirm the results of this methuselah. Now known, this object is placed in Class V.D.1. Does anyone have a relatively small (n ≤ 9) object they can not track to be placed in Class V.F?
| ACORN DATA | ||
|---|---|---|
| Initial Population: 7 bits | Age: 5,206 generations | E.F. = 743.7 |
| Maximum Population: 1,057 bits (in generation 4,408) | M.I.P. = 151.0 | |
| Final Population: 633 bits (consisting of...) | F.I.P. = 90.4 | |
| 34 blocks, 5 loaves, 1 + 3/4 honeyfarms, 8 boats, 2 ponds, 22 blinkers, 24 beehives, 2 barges, 4 + 3/4 t.lights, 2 ships, 1 (8.3), 13 gliders (!) | ||
| Note: during its history, the acorn creates many other types of stable objects including the toad, fishhook (eater), the fleet (4 ships), and biloaves all of which are destroyed before the acorn reaches maturity. This last object was noted by Marshall as evolving in generation 348 from two touching beehives. | ||
Page 13
Page 14

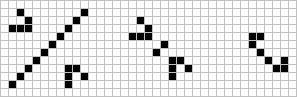
Before discussing the two kingdoms of transfinite objects, I would like to present some interesting Life events in the finite area. These are really Class V patterns since they are unstable and have a finite age. The first of these involves a simple decaying diagonal and a glider to arrive at the configuration discussed on page ten which creates a lightweight spaceship (or, by a slight change in timing, a middleweight one). Like the finite fuse scenario last issue (No.2,p.10) the size of the diagonal and distance of the glider may be as large as one wishes. Another scenario provided by William P. Webb of San Rafael, Calif. involves two gliders racing across space to save a 'dyagonal' (fuse burning at each end). They finally mend the dyagonal by constructing fenceposts on each end.
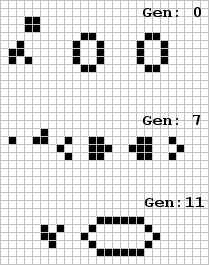
We have previously seen how a pentadecathlon reflects a glider 180 degrees (No.1,p.5), 'eats' a glider (Feb.col,p.114), and 'cooks' a glider into a block (No.3,p.4). The event shown here demonstrates how a pentadecathlon revives a block (which has just been moved by a glider) into a glider which successfully escapes! Does anyone know how to create a block from an oscillaor every fifteen generations? Regarding the reflection of a glider 90 degrees - this is a feat apparently very difficult to do. Gosper found a way to use the twin bees (page four) as a mirror by using a two bit spark created in phase 20 similar to the event given by Webb last issue (page eleven). This last event is shown below.
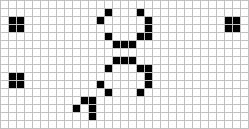
We have also previously seen several ways in which a latent beehive (![]()
Page 15
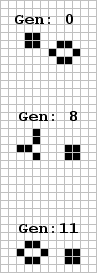
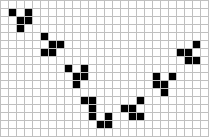
The last two events demonstrate the eater's voracious appetite. Shown to the right is one eater single-handedly absorbing two dense period 14 glider streams by converting the first and all odd numbers of gliders in each stream into a boat which then absorbs the second and all even numbers of gliders in each stream. The next figure shown the eater's ability to consume gliders, as well as light or middleweight spaceships.

It now appears that, in general, the activity regarding transfinite objects is not adequately described using the conventional methods. Further, the characteristics of wicks and agars are different enough to warrant discussing each of them separately. For convenience in describing and comparing the many new discoveries in these two kingdoms, I have proposed new systems of classification as well as some new definitions and measures.
Wicks generally are orthogonal, diagonal, or some other angle (between zero and 45 degrees) to the grid axes. If means are known to provide a boundary for an end of the wick, a finite object of any length can be constructed (for example, the fencepost for the diagonal).
Since absolute size has no meaning for wicks, another measure must be used. I have defined average linear density (ALD) as the number of bits (average) per unit length of wick as a measure of size or thickness. Like finite objects, wicks may be conveniently grouped into six broad classes based upon certain characteristics of their history. A proposed classification system for wicks is shown on the next page.
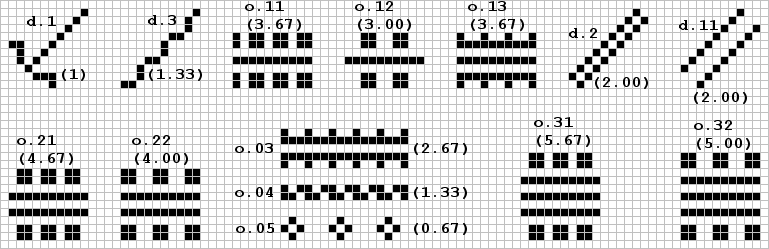
Page 16
| A CLASSIFICATION SYSTEM FOR 'WICKS' (ONE-DIMENSIONALLY INFINITE OBJECTS) | ||||
|---|---|---|---|---|
| Primary Class | Subclassified According To: | Subclass | Example | |
| I-Still | diagonal | |||
| II-Oscillators | Type of periodic activity | flip-flops (all period two) | II.A | barber pole |
| channels | II.B | slow blinkers | ||
| inductors | II.C | U's | ||
| miscellaneous | II.D | C's | ||
| shuttles | II.E | busy bees I | ||
| III-Spaceships | rank | |||
| IV-Propagators | Nature of activity | spaceship guns | IV.A | multi-Gun |
| puffer trains | IV.B | PROPagaTOr | ||
| V-Fuses | Local census | clean | V.A | dyagonal |
| Class I | V.B | harvester | ||
| Class II | V.C | coast guard | ||
| Class III | V.D | HGF-II | ||
| unknown | V.F | Y34 | ||
| VI-Random (active) | Locale of activity | entire edge | VI.A | random rank |
| end | VI.B | random fuse | ||
Using discoveries sent in by readers as well as some examples devised by the writer, the next several pages will illustrate specific wicks in each class.
Class I contains wicks described in previous issues as well as some new ones. They are very common and are shown merely to illustrate the wide variety possible. The symbols (e.g. d.l) will be used later to refer to wick type in discussing fuses. They include the diagonal (the simplest wick), half pond pieces (No.2,p.8), and fenceposts (No.2,p.8) as well as any linear collection of finite Class I objects such as tubs (No.2,p.8) or the product from the harvester (Feb.col,p.115). Note the simple symmetric boundary for the diagonal provided by Woods. Some wicks like the double diagonal need no special boundary for constructing finite lengths. Shown below are some more complex wicks sent in by Skinner (diagonal) and Woods (orthogonal).

Page 17
Class II.A wicks (flip-flops) are fairly common, the barber pole (Feb.col,p.115) being the best known. Shown here is a sample of these wicks illustrating the variety of angle and ALD. Note the finite boundary for the first wick (a bit cumbersome). Also an infinite set of finite Class II objects (blinkers, say) may be used to construct a wick.
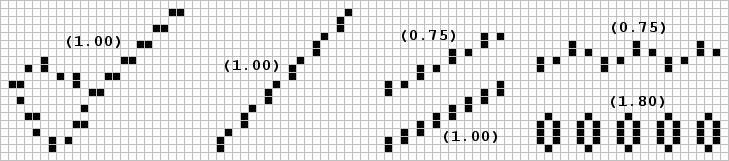

Class II.B wicks (channels) are actually m by ∞ billiard table configurations. Shown at the left are several of these with channel widths from three to five cells. The last five exhibit a phenomenon which the writer calls an 'illusion of motion' (IoM). The pinwheel (Oct.col,p.122) for instance, demonstrates a rotational IoM and as Rudi Krutar of Pittsburg, Pa. points out, two of the rotor's bits appear to be moving with a velocity greater than light. 'forcing one to the conclusion that the pinwheel has the capability to warp space!' Much more will be said about IoM with regard to agars. The active portion of these channels appear to be moving east at the speed of light (actually 1.5C for the tubs!) with a period of one (c) or two (b, d, and e) when actually they are stationary oscillators with respective periods of 4, 5, 10, and 14. Wolfgang Ebenhoh of Heidelbert, Germany sent in the 'impulse conductor' (f) which operates like wick d. One can also vary the length of the active elements of wicks c and e to achieve a similar impulse effect. Boundaries for this class of wick are very difficult to construct (notice the one shown for b).

Class II.C wicks (inductors) are not as common and include the three period three wicks at the left. The first two operate on the same principle as Trawick's candelabra (No.2,p.4) and the diagonal one you will recognize as made of the pulsar quadrants.
Page 18

Class II.D (misc.) includes the period eight 'C's' sent in by Edward Fitzgerald of Irvington, N.Y. which like the tumbler, every four generations turns around. Also in this class is a simple glider stream like that shown on page 15 which incidentally, is of the maximum possible density - spaced 14 generations apart. You might argue the stream moves at (1/4)C with a period of four (IoM) when actually it is stationary with period 14. The Gun and pentadecathlon could be used as the two boundaries for such a wick of period 30.
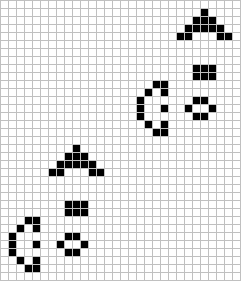

Class II.E (shuttles) include the two busy bee wicks shown here. They each use a different method of mutually annihilating the formed beehives. The diagonal one incidentally, creates large showers of sparks.
 Two spaceships |
Bees |
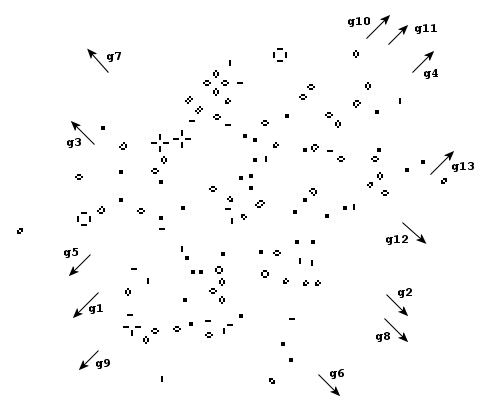
Fitzgerald reported the first true spaceship (Class III) in this kingdom of Life. The 'rank' (my term) is one of many similar configurations where the entire wick moves at the speed of light. Shown here with the rank (period two) is one of its cousins 'R3,5' (period six). Gosper reports an infinite flotilla of B-heptominoes that move at (1/2)C apparently with a period of 20. He has yet to confirm this however because the exhaust gets extremely complicated. Wilson has discovered a spacing that will allow a formation of pi-heptomino cousins to travel at .3C with a period of 30. This last configuration shown here in printout supplied by Bison (see 'bullets') was the subject of investigation by many readers including the writer who were looking for the proper exhaust control to create a finite spaceship.
Page 19
Gliders may be placed in a formation which moves orthogonally at (1/4)C with a period of 20 (minimum) or in a formation that moves diagonally at (1/4)C with a period of four (see example at right). A wick may also be fabricated, of course, from an infinite flotilla of any identical spaceships which move at (1/2)C with a period of four. These may be orthogonal or an angular arrangement although both move horizontally. Shown here is an approximate 18 degree angle.
 A multi-barreled Gun |
 An angular flotilla |
 The PROPagaTOr |
An infinite number of Guns could be laid end-to-end without the blocks to form a multi-barreled Gun (No.2,p.7) which would be a Class IV.A wick creating an agar of gliders! The writer, by modifying the rank has discovered a configuration that creates an agar of blocks while moving at the speed of light! Shown here, the Class IV.B 'PROPagaTOr' (period four) creates its own number of bits every seven generations making it one of the most prolific objects known (finite or infinite).
Page 20
Using any of the Class I through Class IV wicks, we can 'light' (activate) one end and thereby create a Fuse (Class V wick). The active portion of the fuse will feed upon the stable wick at some speed (usually = C). After reaching equilibrium, which usually happens, the burning will occur in periods (usually a multiple of four) converting (period)X(speed)X(ALD) bits into:
| nothing (Θ) | - Class V.A |
| Class I wick | - Class V.B |
| Class II wick | - Class V.C |
| Class III wick | - Class V.D |
In the first case, the rate of change in population is (0-(period)X(speed)X(ALD))/(period) bits per generation. In the last three cases the net rate may be negative, constant, or positive. A single type of wick can be activated and burn many different ways. The diagonal for instance has been reported in at least fifteen different fuses of which several well known are given here:
| decaying diagonal | - Class V.A |
| harvester | - Class V.B |
| beacon | - Class V.D |
The first fuses reported were based on the simple, single diagonal. An amazing variety of fuses have since been reported based on allkinds of wicks including multiple parallel ones. The table on the opposite page summarizes, by subclass, most of the fuses reported to date. Shown are the wick type (as described on page fifteen), burn type (as described below), period, speed, census, and rate of population change for each of the fuses. Some of the new and more unusual fuses will be described and illustrated on the next few pages.

Class V.A consists of the clean burning fuses (a term coined by Woods) and includes besides those described before (Apr.col,.116), the simple looking fuse shown below which after an initial explosion begins burning quietly away with a period of four. The type of burning (see note 10 in the table) is identical to the clean fuse reported by Rosenbaum last issue in the scenario on page ten. As discussed, this burn converts a fencepost boundary (if oriented properly) into a glider heading in the same direction as the burn. Woods has tracks the 'cloudy mass' as he calls it, from the explosion for 519 generations by which time it stabilizes into 3 blocks, 3 beehives, 1 ship, 2 blinkers, and 4 gliders. Bill Woods (Don's father) has nicknamed this fuse the 'reverse fuse' since it explodes first and then burns quietly away.
Page 21
| A SUMMARY OF FUSES | |||||||
|---|---|---|---|---|---|---|---|
| Class | Name | Wick Type | Burn Type | Period | Speed | Census (@ period) | Rate (bits/gen) |
| V.A | dyagonal fuse b reverse Y22 HBF-c cow DBF-c DBF-l GF HTF-c two-or-four rank-c |
d.1 d.1 d.1 d.1 o.11 o.12 o.21 o.22 o.03 o.31 d.11 r.1 |
C 01 10 Y22 C C C C 03 C 06 r1 |
1 4 4 4 18 8 6 8 6 6 2 4 |
speed =C in all cases other than those shown here |
Θ | -1. -1. -1. -1. -3.667 -3. -4.667 -4. -2.667 -5.667 -2. -1.75 |
| V.B | harvester twin boats fuse c baker honeyfarm-II paul bunyon boatwright shipbuilder synapse burning barge-I HGF-I burning barge-II HTF-1 harvester-II rank-b |
d.1 d.1 d.1 d.1 o.04 d.3 d.1 d.1 d.1 d.2 o.13 d.2 o.32 d.1 r.1 |
G5 Y55 O2 G3 O5 O7 G6 ? 11 Y44 C O8 C GC5 r2 |
4 4 4 4 12 6 4 8 4 4 9 8 12 4 4 |
3/4C | block 2 boats 'clouds of debris' loaf beehive pond boat ship block 2 boats 2 blocks 2 boats, 2 beehives 2 blocks block block |
0 +1.5 +0.75 -0.5 0 +0.25 -0.25 0 +0.5 -2.778 +0.75 -4.333 0 -0.75 |
| V.C | coast guard washer woman public works dept detour glider fuse |
d.1 o.05 d.1 d.1 d.x1 |
Y33 O9 G4 Y44 G5/4 |
8 18 8 8 4 |
2/3C | beacon t.light t.light 2 blocks, 2 blinkers glider |
-0.125 +0.222 +0.5 +0.75 -0.75 |
| V.D | HGF-II | o.13 | C | 12 | 2 gliders | -2.833 | |
| V.F | Y34 baker's cousin |
d.1 d.1 |
Y34 GC3 |
? ? |
? ? |
? ? | |
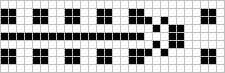
The 'cow' was sent in by Woods who says, 'burns t the speed of light with period eight, eating blocks, bringing them back, and eating them again (chewing its cud)'. Interestingly, many of the orthogonal fuses (single, double, or triple rows bounded by closely packed blocks) burn with a multiple of six rather than the usual 4.
Class V.B now consists of fuses that create sets of all kinds of stable objects (see census column in the table above). The 'burning barge II' on the top of the next page creates twin boats and beehives every eight generations.
Page 22
 The harvesteR |
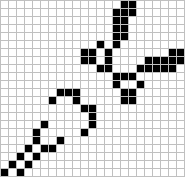 Burning barge II |
 HGF II |
The synapse fuse like the harvester creates a block every four generations but has the unusual property, however, of remaining dormant (stabilized by a fencepost) until a glider strikes its end. Also shown in the fuse scenario last issue was this burn converting a fencepost (with proper orientation) into a glider which departs at a right angle to the original diagonal. Abbe has experimented with burning ranks and reports the fuse shown at the left above which every four generations creates a block. Interestingly, the result is identical to the harvester even though the wick in this case is orthogonal.
Class V.C fuses are not as common as the first two and include the detour fuse which every eight generations creates twin blocks and blinkers. Woods, who sent in this fuse, says, 'I have named this fuse the detour, since it takes straight road, tears it up, and sets up road-blocks with blinkers on them.' This class also includes the glider fuse shown on page eight in the June issue since the gliders produced are in a stream.
Class V.D is very uncommon and only includes the amazing double glider wave fuse discovered by Woods and shown [above as HGF II].
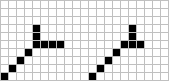
Like finite objects, Class V.F contains fuses whose outcome is not known. Included in this class are the two simple looking fuses shown below provided by Woods. As a challenge to anyone with a good algorithm for tracking fuses, they are presented here. Unlike the acorn, their fate is not known to the writer.
Class VI contains wicks which unlike any others, are constructed of a random configuration and therefore, if activated will never achieve a stable period. Some examples of this somewhat hypothetical class are given below. Robert A. Kraus of Chicago, Ill. sent in the 'n-car train' (third wick).
Page 23

Before discussing agars, I would like to introduce an interesting an yet little explored group of fuses called by their investor, Woods, 'fly by fuses'. These are linear orthogonal strings or collections of finite stable objects. The active portion in this case is propagated by a single heavyweight spaceship passing in close proximity to the wick at just the right timing and spacing. In passing, sparks from the spaceship 'ignite' the latent objects. Shown below is a sequence of figures showing the ignition of one of these objects. In this case a beehive results 36 generations after ignition. Woods, after trying various configurations for the latent 'explosive' has observed byproducts of Classes I, II, and III (also extinction). For example, the slightly different object by only one added bit shown (insert) will, 1239 generations after ignition become 13 blocks, 2 boats, 2 beehives, 1 ship, 8 blinkers, 3/4 t.light, and 3 gliders!

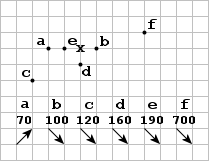
Using the collision mechanism given on page four of the first issue, we could continuously convert a sparse backward wave of gliders (each spaced apart 200 generations in time and 100 units in space) into R-pentominoes using a single heavyweight spaceship. This scenario uses the history data of the R-pentomino (Jan.col,p.105) which is given here in a simple schematic to indicate approximately where, when, and in what direction the six formed gliders (a through f) will be located. At generation zero the heavyweight spaceship meets the first target glider (gl) just crossing the X axis.
Page 24

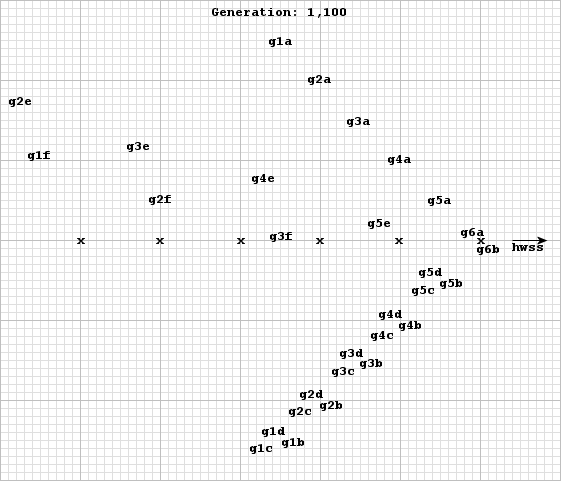
This arrangement is shown above. By generation 200N we would have one heavyweight saceship (still moving east on the X axis), about 6N new gliders (moving in two forward and one backward waves), and about 86N bits consisting of blocks, boats, beehives, ships, loaves, and blinkers in a strip about 50 cells wide and 100N cells long. A schematic of this arrangement is shown below for N = 5.5 or generation 1,100. Notice that 2N of the formed gliders are now traveling in the direction (backward wave) with the same relative timing and spacing as the original target set.
Page 25
The third kingdom of Life regards two-dimensionally infinite objects which for convenience we will call agars. Like wicks, if means are known to provide a stable border, a finite object of any area desired can be constructed. Agars are either stable, oscillatory, or unstable. If unstable, they may be regular and activated either along an edge (infinite) or at a point OR they may be random and active throughout. Since they will the entire field, propagating agars are meaningless. Likewise spaceships have no meaning although one might argue these are possible (as the flotilla given on page nine of the June issue). All apparently moving agars will be referred to as oscillators displaying an illusion of motion (IoM). A specific example demonstrating this phenomenon will be discussed later.
Again, like wicks, absolute size has no meaning for agars and another measure must be used. It is convenient to define a 'unit rectangle' as the minimum m by n area needed to adequately describe the field. I have defined average field density (AFD) as the number of bits per unit area of the agar. Any of the toroidal constructions may be extended o make up an agar. Conversely, a unit rectangle as a toroidal surface will behave in the same way as the entire agar. Agars can also be constructed by laying Class I, II, or III wicks next to each other or by using an infinite field of finite objects.
A proposed simple classification system for the kingdom of agars is given below. Again, using discoveries sent in by readers as well as some devised examples, I will described specific agars in each class. All the work done by readers with toroidal surfaces will be included in this discussion.
| A CLASSIFICATION SYSTEM FOR 'AGARS' (TWO-DIMENSIONALLY INFINITE OBJECTS) | ||
|---|---|---|
| Class | Characteristic | Example |
| I-Still | stable | chicken wire |
| II.A-Bits and Pieces | finite parts that oscillate | square dance |
| II.B-Ripples | infinite parallel rows or diagonals that oscillate | 'sevens' |
| V-Unstable | unstable | 'doomed' |
| VI-'Fuses' | a Class I or II agar activated along an infinite edge | |
| VII-Seeded Agars | a Class I or II agar activated at a point - oval boundary expands | seeded block agar |
| VIII-Broths | initially a field of random bits | primordial broth I |
Class I agars (still) are the most common and include those shown at the top of the next page. The 'chicken wire' (whose border was provided by Skinner) represents one extreme of a family of agars where n (n = 2,3,...) bits in every other row is shifted one row. The other extreme would be a set of parallel rows spaced one row apart. In all cases, these agars have an AFD = 0.5 which is probably the maximum for all Class I agars. Incidentally, the agar formed by the PROPagaTOr (see page 19) has an AFD = 0.2. Woods sent in the 'stockade' figure shown below which can be made as large as one wishes to create an agar of density = 0.5.
Page 26
 Chicken wire (with border) |
 The stockade |
Class II.A agars (bits and pieces) consist of all oscillators except those made of parallel rows or diagonals. The later are in Class II.B (ripples) a name first given to a specific agar by James G. Mauldon of Amherst, Mass. and later to these type of objects in general by Charles Trawick of Decatur, Ga. The five agars discussed last issue (page nine) are all in Class II.A. Tower's agar is unique because its phase three AFD (= 8/14) is greater than 0.5. This is not maximum for any Class II phase but is extraordinary for a Class II.A agar.

The two flip-flop agars (bits) were sent in by Kraus. Fitzgerald reported the agar at the left below which flips over every generation. Kraus, by extending the barber poles on the quad (see page three) constructed the 'trellis' configuration below. The other trellis arrangement illustrates how billiard tables can be used without inductor coils to make agars. The period four 'U's' agar is somewhat like Trawick's candelabra mechanism. The two 'spaceship flotillae' from last issue (page nine) are actually period five and seven (respectively) oscillators.
 Some period two agars |
 A period four agar |
Page 27

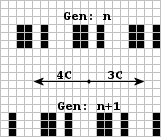
The glider agar shown here (with an AFD = 0.2) appears (IoM) to be a period four spaceship but is actually a period 20 stationary agar. This is certainly not the maximum density for a field of gliders and [I] challenge readers to submit what they think is maximum. I will publish the one with the largest density received in issue Number Four.
Class II.B agars (ripples) all have the same structure (i.e. parallel rows or diagonals) but display an amazing variety of periodicity and AFD and includes all the work done by Donovan Smith of El Cerrito, Alif. and Trawick discussed last issue on page 13. First, I would like to describe a specific ripple which I think adequately demonstrates IoM. The agar at the righ appears in one generation, to be either: moving east with a speed of 3C OR west with a speed of 4C (with a period of one) when actually it is a stationary agar oscillating with a period of seven. This is analogous to the phase velocity of a physical object achieving a velocity greater than the speed of light. You might be interested in reading the article entitled, 'Things that go faster than light' in the July 1960 issue of Scientific American.
Because of their structure, the unit rectangle for orthogonal ripples is a one by n strip. A single strip (1 by 12, say) can support different oscillators as was pointed out in June (page 13). Incidentally, Mauldon points out the period four and period five agars can also exist on a 4 by 11 surface (the period five can also exist on a 4 by 13 surface). Trawick has done an extensive investigation of periodic agars on one by n surfaces. The results of his work and also those of Smith are summarized in the table below. Shown are the specific configurations for all known agars whose strips are 21 or less cells. For strips between 24 and 381 (Smith's largest) only the period is shown and then only if it is different. Smith found many other oscillators with periods the same as those shown. I will run down the list and note anything of special interest.
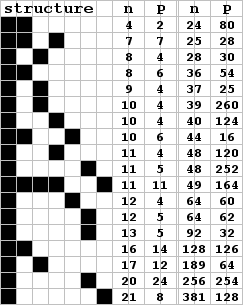
Agars of periods two, seven, and eleven are unique, the later two existing on strips the same size as the period. Interestingly, these three are the only agars to have the same configuration in each of their phases. The period six agar on an eight cell strip achieves an AFD = 0.75 during its cycle which is very likely the maximum for all Class II agars. This is not uncommon though since many of the agars listed achieve this same density in one or more of their phases. Of the nine cell strip, Trawick writes, 'this pattern is the product of every surviving pattern I studied on this field, and at the moment, I can't find a pattern that doesn't survive'.
Page 28
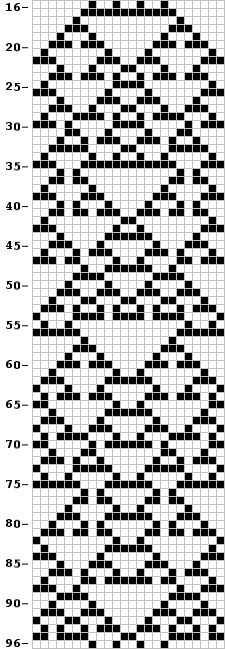
The ten and eleven cell strip each support three different oscillating agars. The period four agar on the twelve cell strip emulates the activity of an infinite flotilla of overweight spaceships. To illustrate the nature of the activity of these ripples, I have presented all the phases of the period eighty agar sent in by Smith. This agar evolves from a 4 by 24 'necklace' (see page 13 in June issue) in 16 generations. Note the density in rows 36 and 76.
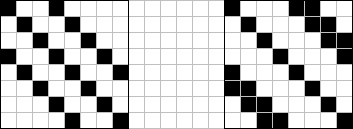
The other type of ripple includes parallel diagonals which usually must be expressed as an m by n rectangle since the diagonal need not be necessarily 45 degrees. Mauldon's agar 'surf' on the next page illustrates this. The three different phases of this period thirty agar are shown. Each third generation a given phase type appears shifted on cell to the east giving the illusion of a 1/3C speed. A period four and period eight agar can exist on a checkerboard size surface as shown below.
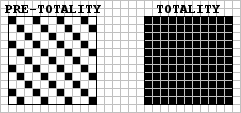
Class V agars (unstable) includes anything not in Classes I or II and could probably be subclassified according to its outcome. Several agars that eventually achieve an AFD = 1. and then, of course, die are shown here. The diagonal one was supplied by Marshall. The orthogonal one, 'doomed' requires a smaller one by n strip to define its structure as it approaches its fate.
Page 29

Class VI agars ('fuses') was defined merely to provide an analogous class to the wick fuses. Actually, you could view this as an active wave front moving through an agar converting it from one form into another. Shown below is a period two agar being converted into a period twenty agar at the speed of light.

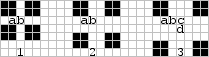
Class VII (seeded agars) include the one discussed by Martin Gardner in Scientific American (Feb.col,p.116) which involved a block agar (AFD = 4/9). Simple regular block agars may or may not be successfully seeded (with a single bit) depending on the AFD and location of the seed. Shown at the top of the net page are the possible seed locations for block agars of decreasing density. Only three of these cases allow the instability to propagate forever through the agar. Case 1.a, as discussed in Scientific American, develops with orthogonal symmetry of order one. Case 2.a, shown on the next page, at generation fourteen is now propagating along an expanding square (?) boundary at the speed of light around a nonsymmetrical active growth.
Page 30
Case 2.b will develop with diagonal symmetry of order one. Cases 1.b and 3.d repair themselves. Case 3.a loses one block, case 3.c loses two blocks, and case 3.b converts one block into a boat. One could start with the stockade (page 26) and as Woods says, 'remove the outer forts (blocks) to give an interesting agar in which each wall in turn crumbles'.

Class VIII agars (broths) are those whose generation zero is composed of a random field of bits.
Page 31

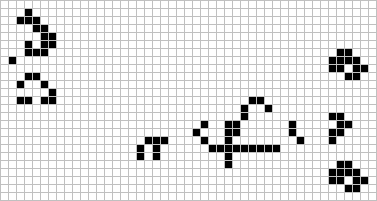
In LIFELINE Number Two (see page 14), I introduced an described IMMIGRATION, a two person game invented by Woods. For anyone who has played the game, the following will be of special interest. Woods has observed a phenomenon in IMMIGRATION that he calls 'alliances'. These are Class II or Class III objects made up of two colors (both players' pieces) which coexist in equilibrium. For example, the blinker at the left 9two states) will exist indefinitely with both players' pieces. Another, more complex alliance exists in the figure-eight oscillator also shown here. Woods has found, and challenges readers to find the only possible allied for of the glider. Unexpected things happen in this analogous three state version of Life, for example, the bicolored (squares and X's) spaceship at the right becomes all O's in five generations! Woods believes allied forms of the three spaceships are impossible.

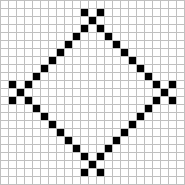
The M.I.T. group have been working on a method for determining the smallest area that should contain a Garden of Eden (GoE) pattern. By means of a new, powerful proof developed by Roger Banks and Steve Ward (with assistance from Schroeppel and Mike Beeler) they have succeeded in showing that an area of only 9 by 33 cells contains a GoE! Additionally, Banks has described a specific configuration he believes is a GoE! This incredible object, which I have named 'the orphan' is shown here to the left.
The puffer trains described previously (page six) which do not have exhaust control (by extra spaceships or trains) exhibit the fascinating ability to achieve an eventual spacial period. Gosper conjectures that if a window showing us a fixed, finite part of the train is moved along with the train at C/2, it will ultimately show us a periodic pattern. Furthermore, this period will be an integer multiple of the period of each subset window. This even applies to the BREEDER. He believes that this behavior is because information tends to travel in exhaust more slowly than C/2 (although it has traveled faster, whereupon it catches the engine and kills the train!), so that periodic active regions tend to pull apart more often than they recombine. While they are apart, portions of them become periodic in time and lose age difference information. Such explanations are known in the trade as 'handwaving'. This discussion extends to fuses in general - one can regard a puffer train as a fuse harvesting a vacuum. The illustration on the next page shows the Puffer Train generating raw matter prior to its developing a spacial period.
Page 32
Conway mentioned that universality implied the existence of a finite arrangement which emits an infinite glider stram representing all the digits of pi. An ordinary Turing machine, or any real computer, using the best method we know for computing pi, would take increasingly long to compute each digit - n digits requiring n(log n)2(log log n) time units. It is an intriguing question whether a Life form could grow more processing mechanism while computing pi, so as to sustain or even increase (!) the rate at which the bits emerge. Whatever the limitations, puffer trains are a boon to machine construction - they can be laying down binary (versus unary) registers (with shift and add logic, etc.) which grow faster than they could be used.
In closing LIFELINE Number Three, I would again like to give indication of additional subjects the writer has in mind and plans to eventually bring into future issues of the newsletter. We have covered a good many of the Coming Events from last issue so in addition to the ones previously mentioned, I add the following:
COMING EVENTS:
- multi-staged fuses
- growth factor - another measure
- types of illusions of motion
- 'perfect fathers' - unique predecessors
- self repairing Life objects
- other special algorithms
- P.I.P. - yet another ratio
- types of inductor coils
- a binary universal turing machine
- some more fly by fuses
- types of billiard table ends
- other eaters
- some more alliances
- rules for ripples
- an atavising algorithm!
- serial Life
- calculating a transcendental number using puffer trains
- more interesting scenarios of Life's events
- elastic perimeter - a measure of area
- objects that completely renew themselves
- visiting every cell in the plane
- some empirical and theoretical broth data
- some interesting results of varying Conway's basic rules
RANDOM BITS: Due to the late date in sending out this issue, I am withholding LIFEFILE which was meant to include a current summary of Thompson's work. In terms of shear magnitude of numbers, here is what is known: 160 n-ominoes - all thru 7, 15% of 8's, 640 kingwise - all thru 6, 2755 spatial - all thru 5, 30% of 6's. Thompson notes 306 different predecessors to the beehive, more than any other object. Of the 108 heptominoes, 30% go to beehive or its form (e.g. honeyfarm). He has found 21 primary methuselahs. There are 192,622,052 different 18-ominoes! Errata: p.8 ≤ should be ≥ / p.12, 2 ships s.b. 3 ships
Page Scans
 Page 1
Page 1 Page 2
Page 2 Page 3
Page 3 Page 4
Page 4 Page 5
Page 5 Page 6
Page 6 Page 7
Page 7 Page 8
Page 8 Page 9
Page 9 Page 10
Page 10 Page 11
Page 11 Page 12
Page 12 Page 13
Page 13 Page 14
Page 14 Page 15
Page 15 Page 16
Page 16 Page 17
Page 17 Page 18
Page 18 Page 19
Page 19 Page 20
Page 20 Page 21
Page 21 Page 22
Page 22 Page 23
Page 23 Page 24
Page 24 Page 25
Page 25 Page 26
Page 26 Page 27
Page 27 Page 28
Page 28 Page 29
Page 29 Page 30
Page 30 Page 31
Page 31 Page 32
Page 32