Lifeline Volume 1
| Lifeline Volume 1 | ||
| ||
| Published in | March 1971 | |
|---|---|---|
| Succeeded by | Volume 2 | |
| This page is a transcript of Volume 1 of the Lifeline newsletter |
|---|
| This article may contain spelling mistakes and/or errors that will not be corrected -- it is preserved in this way for history's sake |
A QUARTERLY NEWSLETTER FOR ENTHUSIASTS OF JOHN CONWAY'S GAME OF LIFE O OOOOO OOOOO OOOOO O OOOOO O O OOOOO O O O O O O OO O O O O OOO OOO O O O O O OOO O O O O O O O OO O OOOOO OOOOO O OOOOO OOOOO OOOOO O O OOOOO Number 1 MARCH 1971• Editor and Publisher: Robert T. Wainwright •
Page 1
What you are now reading is the prototype issue of LIFELINE, a newsletter for enthusiasts of John Horton Conway's game of 'Life'. Scientific American having already devoted two full Mathematical Games columns to this subject can not, obviously, continue to provide the space required to report adequately on all the new developments still occurring. Many readers (the writer included) have expressed an interest to have some means by which they may continue to exchange new developments. My own prior investment of time and effort motivates me to establish this newsletter and I will maintain it in proportion to the degree of interest expressed by you, the 150 correspondents of Martin Gardner's October 1970 and February 1971 columns.
This first newsletter is compiled from information contained in your letters to Martin Gardner and from experiments conducted by the writer. Subsequent newsletters will necessarily depend upon the extent of your response to LIFELINE. A subscription form is provided abreast of new Life developments. I will attempt to provide an interesting mix of information in a free format and solicit your comments and suggestions on how this could best be done.
John Conway first presented his game of Life to Martin Gardner early last year. At that time he had followed the life histories of all but one of the pentominoes, all but one of the hexominoes, and all but seven of the heptominoes. By now we all know the fate of the notorious R-pentomino which, in its first generation, becomes a hexomino (the one who's fate was unknown to Conway). This apparently confused a number of readers who wondered how Conway could have known about all the hexominoes as stated on page 122 of the October column.
This leaves us with the seven 'unknown' heptominoes shown here which Conway arbitrarily labeled B, C, D, E, F, H, and I.

Heptomino B whose first generation appears in the 29th generation of the R-pentomino eventually becomes three blocks, one ship, and two gliders after 148 generations - so its history is known. This was confirmed by Mr. Hugh W. Thompson of Lefrak City, New York.
Page 2
Heptomino C has the same history as B after two moves - so its history is also known. Heptomino D which Conway calls Herschel, after the astronomical symbol ♄ for Uranus appears in the life histories of B (and C) and evolves into two blocks, one ship, and two gliders after 128 generations. If anyone knows this histories of the remaining four unknown heptominoes I shall be pleased to report their results in the next (Number 2) issue of LIFELINE.
Life 'objects' may be conveniently grouped into one of six classes based upon certain characteristics of their history as shown below with a specific example for each of the first four classes. Class V which really includes all known unstable objects is expanded showing final outcomes of the n-ominoes up through n=7.
| A CLASSIFICATION SYSTEM FOR 'LIFE' OBJECTS | |||||||
|---|---|---|---|---|---|---|---|
| O B J E C T S |
Characteristics of Life History | Class | Age | Example | |||
| Stable | Inactive | Class I Still Lifes |
∞ | block | |||
| Active | Stationary | Class II Oscillators |
∞ | blinker | |||
| Moving | Constant Bits | Class III Spaceships |
∞ | glider | |||
| Increasing Bits | Class IV Glider Guns |
∞ | Glider Gun | ||||
| Unstable | Predictable | Class V All Objects Not In Above (Known) |
varies | n-ominoes | |||
| Unpredictable | Class VI All Objects Not In Above |
? | broths | ||||
| Note: All Class V objects either die or evolve into object(s) of Class I, II, III, or IV. The number of n-ominoes becoming one of these final classes is shown for those cases known. | ||||||
| Class V Object | Number That Die | Number That Evolve Into: | Total Number of n-ominoes | |||
|---|---|---|---|---|---|---|
| Class I | Class II | Class III | Unknown | |||
| Domino | 1 | • | • | • | • | 1 |
| Trominoes | • | 1 | 1 | • | • | 2 |
| Tetrominoes | • | 4 | 1 | • | • | 5 |
| Pentominoes | 5 | 2 | 4 | 1 | • | 12 |
| Hexominoes | 14 | 14 | 6 | 1 | • | 35 |
| Heptominoes | 27 | 52 | 18 | 7 | 4 | 108 |
Page 3
One of the most intriguing unsolved combinatorial problems in mathematics concerns polyominoes. A general formula is not known for determining the number of different n-ominoes but you might be interested in knowing there are 369 different octominoes, 1285 different nonominoes, and 4655 different decominoes! An excellent reference on this subject is a book by Solomon W. Golomb called Polyominoes published by Scribner's.
Those few n-ominoes that eventually become objects of Class III (irrespective of any Class I and/or Class II objects left behind) seem to be the most fascinating because one or more gliders successfully escape during their history. Mr. Robert J. Maas of Mountain View, Calif. has found an undecomino (eleven rookwise-connected bits) of this type. After only four generations ![]()

The impact of the M.I.T. discovery unfortunately, may have caused many readers to abandon further experimentation with Life. I feel there are yet many exciting new discoveries to be made which do not necessarily require the use of a computer.
One reader, Mr. Curt Gibson of New York City, in fact suggests that two or possibly three independent results done manually will sufficiently verify a particular result. Along this line, I would like to mention that I have catalogued a wealth of information regarding various events (glider-target collisions and Class V object life histories). Verification by several readers, whether done by computer program or manually would save an enormous effort which many including myself have expended. Since the amount of information is so large and the interests of each of you is varied, I will report in the newsletter only an index of what has been done. As an adjust to the newsletter which is aimed at the general readership I will, upon request, send copies of data in your particular area of interest. A comprehensive list of this information (called the LIFEFILE) is attached to the newsletter for you to indicate specifically what you may desire.
Page 4
The February column illustrates (page 113) a 28 bit pattern that will create the Glider Gun. This is the exact information that the M.I.T. group forwarded to Martin Gardner via a set of 28 coordinates last November to confirm their discovery of a glider gun. The number can easily be reduced to 27 and the writer has discovered a 26 bit pattern that will evolve into the Gun. As a challenge to those interested in 'predesesor' patterns of the Glider Gun, I pose the following question: what is the smallest pattern (minimum number of bits) required to generate a Glider Gun. I will report any results received in addition to the 26 bit pattern in the next issue of LIFELINE.
I would now like to report some findings of unusual interest by readers who were not included in the February column. These are not in any particular order but I think they do represent the diversity of phenomena that exist in Life.
The subject of colliding spaceships is indeed fascinating and one which can be extensively investigated without the need for a computer program. Some interesting findings include a result Mr. Joe Becker and Mr. Ray Tomlinson sent showing two lightweight spaceships colliding to yield two gliders. Messrs. Lee Erman, Rudi Krutar, and Eric Werme of Carnegie-Mellon University in Pittsburgh, Pa. report one method of altering a glider's flight path (in both space and time) by striking it with another glider. The writer has discovered a way to convert a glider into an R-pentomino (and therefore subsequently into six gliders, etc.) using a heavyweight spaceship which escapes intact. These results are shown below.
| Lightweight to featherweight spaceship conversion | Glider flight path alternation |
|---|---|
 |
 |
| Creation of an R-pentomino | |
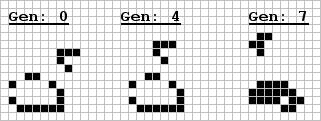 | |
Page 5
Oscillators with a period greater than two (flip-flops) are uncommon. An unusual, and thus far the only oscillator of period five was discovered independtly by Mr. Sol Goodman of Rio Piedras, Puerto Rico and Mr. Arthur C. Taber of Fayetteville, N. Carolina who named it 'octagon II'. The M.I.T. group reports a period three oscillator which is unlike any of the five general types (Subclass II) known. These two new oscillators are shown here.
| Octagon II | An unusual oscillator |
|---|---|
 |
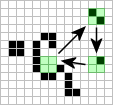 |
The writer has arranged all type II objects into these subclasses:
II-A Flip-Flops: all period two oscillators (e.g. toad, clock).
II-B Billiard Table Configurations: oscillators where the activity is confined within a rectangular area supported on the outside by 'inductor coils' (e.g. pinwheel, Hertz oscillator).
II-C Inductors: oscillators of one or two-way orthogonal symmetry which depend upon mutual symmetry to exist (e.g. Pulsar CP 48-56-72, tumbler).
II-D Pulsators: oscillators which generally have a longer period and appear to expand and contract (e.g. figure-8, pentadecathalon).
II-E Shuttles: oscillators with the longest periods and which contain an active element that travels back and forth (e.g. queen bee, two pentadecthalons shuttling a glider). These last two examples which may be new to most of you are shown here.


Page 6
The harvester (February column page 115) is one of many similar type of phenomena which the Honeywell group have aptly named 'fuses'. Shown here are two fuses with a 'Y' type pattern on the 'burning' end. The fuse on the right produces a beacon every eight generations. Like the harvester, the total number of bits is preserved (ignoring, of course, the beacon effect). The larger 'Y' pattern on the left produces twin boats every four generations thereby increasing the population (by 1.5 bits/gen). Fuses remain an unexplored area and one which can be easily investigated on graph paper. What seems to be happening from almost any starting configuration ('Y', 'X', or whatever) is an eventual evolution into a repeating cycle (usually a multiple of four). The byproducts from this cycle then either die or produce some Class I or Class II object.
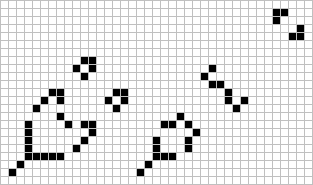
Extremes in population during an object's life history seem to vary considerably with a record being set by the aforementioned 26 bit pattern that grows without limit (at an average rate of 0.167 bits/gen). Mr. Clive J. Tooth of London, England points out that the maximum population (of 319 bits) during evolution of the R-pentomino occurs in generation 821. This must set a record value of (maximum population/initial population = 63.8) for any known Class V object. Incidentally, the writer knows of three other five-bit objects with the same value. The tetromino ![]()
![]()
Mr. Don Woods of Natick, Mass. has defined 'evolutionary factor' as the ratio of age to initial size for an object of Class V. For example, the R-pentomino has an E.F. value of 220.6 (= 1103 generations/5 bits). Surprisingly, this is not the maximum for all five-bit objects. Mr. Woods challenges readers to beat this value before I present his result in the next issue of LIFELINE.
Page 7
O OOO OOO OOO OOO OOO O OOO O O O O O O O O O O OO OO OO O O OO O O O O O O O O OOO OOO O OOO O OOO OOO OOO A COMPREHENSIVE FILE OF INFORMATION GENERATED BY LIFE EXPERIMENTERS
LIFEFILE, an appendix to LIFELINE, is aimed at providing a reasonably complete and up-to-date listing or index of known Life events. These events are presented here in two sections with the intent to just outline the scope of what has been done. The table below summarizes all known collisions involving a single glider striking a simple 'target' (which may also be a glider). At what point the glider and target become one 'object' is an open question and one I intend to discuss in a future issue of LIFELINE. The table on the next page lists all known Class V object life histories. These are presented as families of objects with a particular structure (e.g. size n rows).
Page 8
| KNOWN COLLISIONS INVOLVING A GLIDER STRIKING A TARGET | ||||||||
|---|---|---|---|---|---|---|---|---|
| Target | Direction of Glider Approach | Number of Different Collision | Number Known | Target | Direction of Glider Approach | Number of Different Collision | Number Known | |
| block | any | 6 | all | ship | end | 6 | all | |
| tub | any | 6 | 〃 | ship | side | 7 | 〃 | |
| boat | front | 6 | 〃 | pond | any | 8 | 1 | |
| boat | side | 13 | 〃 | blinker | any | ? | 2 | |
| boat | rear | 6 | 〃 | pentadec. | end | ? | 2 | |
| beehive | any | 13 | 〃 | glider-α | A | 22 | 4 | |
| snake | head-on | 14 | 〃 | glider-α | B | 21 | 3 | |
| snake | thru-slit | 13 | 〃 | glider-α | C | 11 | 3 | |
| barge | end | 6 | 〃 | glider-β | A | 10 | 2 | |
| barge | side | 7 | 〃 | glider-β | B | 9 | 3 | |
| Collision path detail for cases when target is a glider | ||||||||
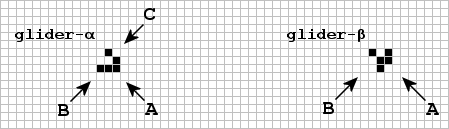 | ||||||||
| KNOWN CLASS V OBJECT LIFE HISTORIES | ||||
|---|---|---|---|---|
| Object Type | Example | Number | Available Data For: | Note |
| n orthogonally connected bits | 55 108 |
n ≤ 6 n = 7 (all but 4) |
these are the n-ominoes listed bottom page two | |
| n diagonally connected bits | 55 | n ≤ 6 | these are the n-ominoes rotated 45° | |
| n orthogonally and diagonally connected bits | 1 12 70 |
n = 3 n = 4 n = 5 |
||
| size n patterns (spatially connected) | 3 5 44 |
n = 2 n = 3 n = 4 |
although not all known there must be about 500 different patterns of 5 | |
| size n rows | - | n ≤ 25 | ||
| size n row pairs (separated by one empty row) | - | n ≤ 19 | ||
| size n row triplets (each separated by one empty row) | - | n ≤ 19 | ||
| m sets of fives in a line | - | m ≤ 7 | ||
| m sets of size n rows in a line | - | n ≤ 9, all m n = 10, m = 2 |
the results are easily predictable for all m | |
| blocks (n×n) | - | n ≤ 9 | ||
| right triangles (side=n) | - | n ≤ 14 | ||
| pyramids (base=n) | - | n ≤ 9 | ||
| squares (n×n) | - | n ≤ 9 | ||
Page Scans
 Page 1
Page 1 Page 2
Page 2 Page 3
Page 3 Page 4
Page 4 Page 5
Page 5 Page 6
Page 6 Page 7
Page 7 Page 8
Page 8