Lifeline Volume 4
| Lifeline Volume 4 | ||
| ||
| Published in | December 1971 | |
|---|---|---|
| Preceded by | Volume 3 | |
| Succeeded by | Volume 5 | |
| This page is a transcript of Volume 4 of the Lifeline newsletter |
|---|
| This article may contain spelling mistakes and/or errors that will not be corrected -- it is preserved in this way for history's sake |
A QUARTERLY NEWSLETTER FOR ENTHUSIASTS OF JOHN CONWAY'S GAME OF LIFE O OOOOO OOOOO OOOOO O OOOOO O O OOOOO O O O O O O OO O O O O OOO OOO O O O O O OOO O O O O O O O OO O OOOOO OOOOO O OOOOO OOOOO OOOOO O O OOOOO Number 4 DECEMBER 1971• Editor and Publisher: Robert T. Wainwright •
Page 1
LIFELINE Number Three met with overshelming enthusiasm as evidenced by your many kind letters expressing praise and interest. Thank you for all the encouragement, just keep responding with results of your own work.
As incredible and fascinating as Life is, I really cannot invest another year of time and effort in publishing LIFELINE. That is not to say however, that the 'lifeline' will be cut off. On the contrary, I believe it will not only survive but thrive -- on the efforts and ideas of fresh input from a new staff. I am, therefore, turning over the responsibility of editing and publishing the newsletter in 1972 to the individual (or group) expressing the most readiness. If you are seriously interested in assuming this responsibility, please write or call me so that necessary arrangements can be made in time for issue Number Five in March. I will provide the address list of readers, all correspondence files, startup assistance, and continuing editorial consultation. Who knows? We might get a writer who knows how to spell!
| Corderman's amazing Switch Engine (with stabilizer) |
|---|
 All aboard the Class IV limited! Last seen it was travelling NW at 15,523.41666--- miles/sec. After humping for 2049, it regularly discharges passengers, born within period 384. These 5 with A tickets race ahead just north of the tracks but 54 B holders are stranded. Of the send off crowd 218 remain. Thirty have departed toward 3 of the double compass points. p.s. Last seen at gen 5533 on a 512 x 512 array. |
As in previous issues, I will first cover the area of Life dealing with finite objects and events, then activity regarding wicks and agars, and finally other selected areas of cellular automata.
My catalogue of Class I objects is slowly increasing. As a confirmation, I would be interested in receiving all known 10 and 11-bit still life objects. Results of the reader submitting the largest set will be published in issue Number Five. In fact, let's also include object sets of 12, 13, and 14 bits.
Page 2
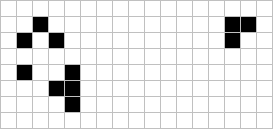
After further consideration, I have concluded that Class II.A should be subdivided into flip-flops (constant size) and on-offs (constant symmetry/alternating size). An example of each of these is shown here both for illustration and to introduce two more new period two objects. Dean Hickerson of Davis, Calif. suggested the 5 by 5 flip-flop and the writer devised the on-off while experimenting with a 6 by 6 area.
Classes II.B through II.F have nothing really new to report since before.
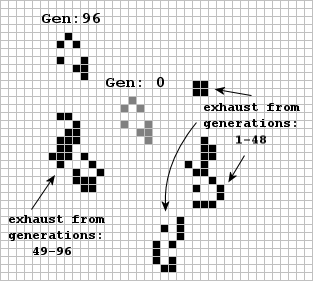
The pattern on the cover page of LIFELINE Number Four includes the incredible 'Switch Engine' named by its discoverer, Charles L. Corderman of Winchester, Mass. The eight-bit pattern on the left, if by itself, has the Class III property of every 96 generations reproducing itself in a location shifted eight cells to the northwest giving it a speed of C/12! The Switch Engine's action is well illustrated in the printout provided by Robert Bison of Hopewell Jct., N.Y. which shows its positions at generations 9 and 96. During its basic glider cycle of 48 generations, the Switch Engine creates unstable residue which advances orthogonally at C/2 giving it the ability on the average to travel diagonally at C/4. After about 12 full periods (generation 1,170), the advancing Switch Engine is ruined by an up and leftward rising pattern which finally stabilizes by generation 3,911.
Subsequently, Corderman found that by placing a block in the 'smoke' of the Switch Engine at just the precise location, the pattern would eventually stabilize into a puffer train!! The entire pattern as shown on page one is in the exact form as received by the writer and gives the original trian, TYpe 1, in the shortest time found so far. Its startup residue stabilizes at generation 741 after which every 384 generations its stable puffer product consists of 3 blocks, 1 boat, 2 beehives, 1 ship, 1 loaf, 4 blinkers, and 1 glider! Interestingly, the glider's direction is identical to the train (northwest). Can the reader determine the period of the resultant glider stream? The starting pattern below gives the simpler Type 2 train which after stabilization creates 8 blocks every 288 generations.

Page 3
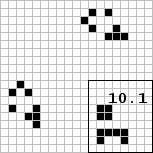
Corderman also discovered ten different tandem combinations of twin Switch Engines that travel together to form a diagonal puffer train! He found the engines could be placed in the same orientation or in a mirror arrangement so long as the active exhaust generated by each would properly react to form periodic stable puffer product. Various periods and associated sets of puffer product were identified. Of these, the most interesting results from the compact tandem arrangement shown at the right which every 1,344 generations (!) yields: 42 blocks, 2 boats, 14 beehives, 2 ships, 8 loaves, 2 long boats, 2 (10.1 - see insert) 2 h.farms, 20 blinkers, 4 t.lites, 2 at.lites, 1 beacon, 2 gliders-nw, 1 glider-ne, and 1 glider-sw!!
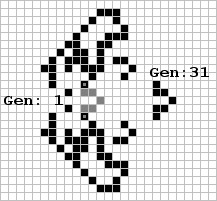
In the very first Scientific American column (October 1970) on page 122, Martin Gardner mentioned the pi-heptomino. Although its history was already known even then, this object has been the subject of investigation by more readers than any other object or pattern reported. The reason is because its first generation appears again in generation 31, but advanced forward nine cells! However, it has thrown off an exhause which by generation 61 interacts and prevents the seven-bit 'spaceship' from reappearing again in generation 61. This orthogonal events (speed=0.3C) is analogous to the diagonal even (speed=C/12) observed in Corderman's Switch Engine. The infuriating problem, obvious to many readers, is due to the excessive exhause created. Many attempts have been made to 'tame', 'poison', 'seed', etc. this nasty exhaust. Of all these, the method devised by Mike Beeler of the M.I.T. group and shown here (right) seems to hold the most promise. The 'spaceship' will move to the right at 0.3C, appearing again in generations 31, 61, and 91. Unfortunately it never makes it to generation 121. Again, notice the similarity to the way in which Corderman successfully stabilized the Switch Engine.
No one responded to the problem regarding the speed at which a wave of glider collisions will propagate up the Y axis given their sources are receding at C/2 along the X axis (see No.3,p.7). The M.I.T. group have determined this value to be C/6.
Page 4
The LIFEFILE this issue contains a summary by size, structure, and symmetry of the histories (age and final census) of practically all known Class V objects. Hugh W. Thompson of Lefrak City, N.Y. has carefully recorded this information for over 8,000 different objects! With census data complete for all objects of six-bits or less, it is now possible to identify the special set exhibiting extreme values of all the previously defined ratios.
The maximum value for the F.I.P. ratio (see No.3,p.8) set by the five-bit R-pentomino and its predecessors wwas not surpassed by any six-bit object. In fact, all six-bit R-pentomino predecessor have the same maximum value of F.I.P. = 19.33. Corderman's acorn (see No.3,p.12) with a F.I.P. value of 90.4 probably sets the maximum for all seven-bit objects. The Switch Engine (alone) has a F.I.P. value of 105.25, the highest yet reported for any eight-bit configuration. And now, for all patterns larger than an incredibly mere ten-bits, the maximum F.I.P. value is infinite!

In the second issue on page 13, I discussed the ratio of age to initial population (evolutionary factor) for Class V.A. objects. The object at the right is one of eight found by THompson that manages to stay alive for 46 generations before death (E.F.=7.67). The diehard (No.2,p.13) still holds the all time record with its age of 118 generations (E.F.V.A. max=14.75).


Class V.B includes the seven-bit object below which has to be the most amazing predecessor to the beehive. Discovered by THompson, the 'Procrestinator' (my term) requires a lengthy 76 generations for its seven-to-six bit transformation! This must set a record for E.F.V.Bmax=10.86. James F. Harford of Topanga, Calif. submits the eight-bit object at the right which in eight generations forms four loaves or by his terminology, the 'bakery'.

Thomnpson reports the Class V.C object at the left which sets the age record for all known objects resulting in a finite (i.e. no gliders) 'constellation' (my term for a large, mixed census - usually from a Methuselah). After 608 generations, this six-bit object stabilizes into 6 blocks, 1 loaf, 3 blinkers, and 1/2 + 3/4 + 1 t.lites (E.F.V.C max=101.33) all lying within a rectangular area of 31 by 48 cells. Interestingly, the pi-heptomino constellation (also Class V.C) lies within a rectangular area of 31 by 47 cells. The record area for any finite constellation is presently held by the 33-bit row whose census after 580 generations occupies an area of 133 by 190 cells! At about generation 390 Corderman notes a census of 32 blocks, 8 ships, 8 loaves, 8 blinkers, and 4 gliders. The two pairs of gliders finally collide and make four more blocks thereby extending the age and area of the resultant 272-bit constellation.
Class V.C also includes the interesting census formed by evolution of two pi-heptominoes or 'blasting caps' as the M.I.T. group call them. The arrangement at the right will, after 304 generations result in 6 blocks, 4 beehives, 2 blinkers, and 2 spark coils (see No.3,p.3)!
Page 5
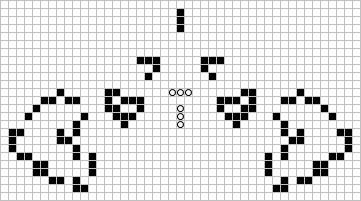
Of all the Class V.C Methuselahs descovered by Thompson during his investigation of six-bit object histories, the twin blinker arrangement above (circles) is probably the most spectacular. Terms the 'thunderbird' because of its later resemblance (generation 155 shown) to the indian emblem, this object survives for 243 generations which is very unusual for a small symmetric object. The Thunderbird's census consists of 2 boats, 4 beehives, and 4 blinkers, one of the very few ever reported not containing blocks.
Before discussing some new Class V.D.1 objects, I would like to correct the acorn data presented in page 12 of the last issue. The age is 5,206 generations and the census should read 23 beehives and 3 ships.

Last issue on page nine a 20-bit Class V.D.1 object was described that spawned a dozen gliders. More recently, James Seawright of New York, N.Y. has discovered a nonomino that is a predecessor to the 20-bit object making it an even more prolivic finite glider generator. In fact, both the son and grandson of the nonomino, although not true objects in themselves, are only eight-bits which increases the ratio of gliders per initial bit to 1.5! The Gun from its minimumj predecessor configuration (No.2,p.6) would have to operator for about 1,200 generations to achieve the same ratio!
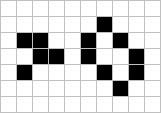

The next two objects are more like events and would normally be presented as scenerios but since the census in each case includes gliders, I will describe them here in Class V.D.1. These were both provided by the group at M.I.T. The first of these is shown as the collision of a glider with the eight-bit object present last issue on page two and also appearing in the acorn constellation (almost exact center). The final census of this collision contains a pentadecathalon! Formed in generation 1,979, this 'natural pentadec' manages to survive amidst much activity which finally subsides by generation 2,585 into: 30 blocks, 1 tub, 12 boats, 18 beehives, 1 ship, 6 loaves, 1 pond, 18 blinkers, 1 toad, 1 pentadecathalon, and 4 gliders! Gosper notes: 'the last glider formed (generation 1,103) makes an amazing escape'. Another interesting event discovered by the M.I.T. group involves the reaction of a pi-heptomino and a boat to yield only a single glider and a 14-bit 'S' shaped still life. The initial arrangement and the Class I object formed are shown here at the right.
Page 6

Of all the R-pentomino predecessors mentioned on page four, the one shown at the right is one of four found by Thompson that has an age of 1,108 generations and therefore the largest evolutionary factor for all six-bit objects (E.F.=184.67). Note the structural similarity to the acorn.



Class V.D.2 (pure glider generators) includes this arrangement of 4 five-bit rows which in seven generations forms 4 five-bit gliders headed for the four corners of the plane. Thompson submits what is probably the 'world's smallest 2-glider generator'. Shown at the right, the G-meson (his term) becomes a decomino before creating a 90 degree pair of gliders. Curt Gibson of New York, N.Y. sent in the collision below which results in a single glider and illustrates how a glider can be reflected 90 degrees - at the expense of one toad, however! Gibson also reports the glider-blinker arrangement here which after a temporary set-back (12 generations) and loss of the blinker, results in a glider which is elevated 4 cells higher. Generation two of this history is a duodecomino.
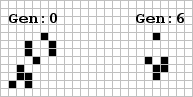
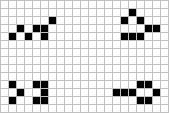
We finally got a response to the challenge (No.1,p.4) of finding a minimum predecessor to the Gun (Class V.E). The result was well worth waiting for because we got a pattern significantly less than the expected 25 bits (No.2,p.6). Corderman managed to find several shuttle predecessors which are smaller than the standard nine-bit minimum, including one of a mere seven bits! These are shown here. Fortunately, one of the eight-bit predecessors and the unique new seven-bit minimum matched to give the required timing of the resultant shuttle combination thereby allowing Corderman to assemble a configuration of only 21-bits! This is shown below. Out of the astronomical number of possible four-glider collisions do you suppose one might just happen to result in assembling the Gun?

Last issue involved an extensive discussion of transfinite objects (i.e. the kingdoms of wicks and agars). Consequently, in this issue, I am limiting this area to only a few subjects.
Page 7
Thompson reports the simple orthogonal Class V.A blinker fuse at the right which burns at an unusual speed of 4/5C with an extraordinary period of five!
The two 'unknown' fuses presented in Class V.F (No.3,p.22) have been successfully tracked to a periodic burn. The results, first reported by Corderman are as follows:
| Name | Class | Wick Type | Burn Type | Period | Speed | Census (@ period) | Rate (bits/gen) | Startup Generation |
|---|---|---|---|---|---|---|---|---|
| Y34 | V.B | d.1 | Y34 | 8 | C | 2 beehives | +0.5 | 243 |
| baker's cousin | V.C | d.1 | GC3 | 8 | C | 3 blocks, 1 beehive, 3/4 t.lite | +2.375 | 468 |
The baker's cousin is the first fuse to be reported with a census containing more than two types of object. Corderman also tracked the 'ignition smoke' from each of these fuses and reports:
| Name | Age | Census |
|---|---|---|
| Y34 | 2,381 | 38 blocks, 6 boats, 16 beehives, 4 ships, 6 loaves, 28 blinkers, and 11 gliders! |
| baker's cousin | 2,050 | 56 blocks, 3 tubs, 10 boats, 22 beehives, 2 ships, 5 loaves, 1 long boat, 1 pond, 3 h.farms, 1 fleet (4 ships), 41 blinkers, 3 t.lites, and 7 gliders! also 2 toads. |
Another reader, Harvey Lerman of Maitland, Fla. tracked the two fuses precisely as they were shown (i.e. as 10 and 9-bit objects respectively) and found these interesting results:
| Name | Class (finite) | Age | Census |
|---|---|---|---|
| 10-bit kingwise | V.D.1 | 190-200 | 3 blocks, 1 ship, 1 blinker, and 3 gliders |
| 9-bit kingwise | V.C | 225-250 | 2 blocks, 1 boat, 2 beehives, 2 loaves, and 1 blinker (temporary toad 144-175) |
Page 8
For anyone with an algorithm for tracking objects on a toroidal survace, I present two deceivingly 'simple' objects for verification of final periodicity (and associated census). The first of these was suggested by Gosper and given on page 18 of the last issue (see bees) and can be tracked on a surface which is only twelve cells wide. The required length of the surface, however, must be approximately one-half the object's age since it travels at C/2 leaving an exhaust which gets extremely complicated. The other object (bottom right of page 7)suggested by the writer, is even smaller and can be tracked on a surface only six cells wide. The required length in this case, however, must be approximately equal to the object's age since it travels at the speed of light leaving an exhaust which like the twin heptomino arrangement is also very complicated. The starting configurations of these two objects are shown. They are presented not so much as a challenge but because the writer is sincerely interested to know if they can be tracked to a final proven period (and census).
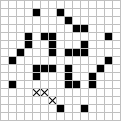
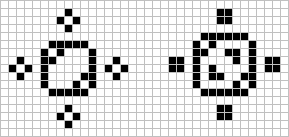
Regarding IMMIGRATION (No.2,p.14 and No.3,p.31), Frank M. Liang of Northridge, Calif. and Dale Edwin Cole of San Barnardino, Calif. were the two readers to sucessfully find the only possible allied form of the glider which is shown here in all of its phases. Liange also sent in a proof showing allied forms of the three spaceships are immpossible. Woods reports the new alliance at the right which he says, 'suggests there is more than one form of Life in Kok's galaxy'. The four arms are completely independent of each other, and any combination of solid (solid) and split (solid,X) arms is feasible.
The Garden of Eden pattern presented last issue around much interest, in part due to Martin Gardner's discussion in the November column. Incidentally, on page 120, the Orphan's size should have been stated as 9 by 33 cells. The Orphan's fate is not nearly as spectacular as its uniqueness, however. Liang reports a rather mundane census of 5 blocks, 1 pond, and 3/4 t.lite after only 134 generations. The Honeywell group using Atavist (an algorithm developed by Woods for backtracking patterns) and about 50 hours of solid computer time, has verified the Orphan to be fatherless!
Of all the variations to Conway's basic rules (with the same neighborhood), the following very simple rules seem so far to be the most interesting: 'a cell will be on (i.e. occupied) in the next generation if and only if it presently has 3 or 4 neighbors on'. In standard context this means 3 or 4 bits for birth and 3 or 4 bits for survival. Rici Liknaitzky and Steve Ward of the M.I.T. group while working with a general rule program written by Roger Banks (now at Vanderbilt University) noticed the unusual variety in this '3-4' version of Life. They have experimented and documented many forms including:

Page 9
- Class I - the block, the only stable form known.
- Class II - many oscillating objects of periods 2, 3, 4, 6, 10, and 12 (several infinitely extensible).
- Class III - a period 3 orthogonal spaceship!
- Class IV - ?
I have shown only one example (bottom of page 8) to illustrate these new rules and so you may enjoy experimenting with 3-4 Life on your own. Issue Number Five will present any reported findings in addition to some of those already known.
COMING EVENTS:
- announcement of the new staff and subscription procedures
- dependent and independent Class II.C phases
- Class II objects illustrated as a density function
- the Class I doublets and quadruplets
- concentrating glider streams
- 'fencing in' inductors
- some empirical Class V data
- some potential puffer trains
- some more pseudo spaceships!
RANDOM BITS: Many readers, too numerous to mention, have tracked the newsletter masthead. To save unnecessary effort on the part of others so inclinded: it stabilizes after 58 generations into 3 blocks and 1 beehive.
O OOO OOO OOO OOO OOO O OOO O O O O O O O O O O OO OO OO O O OO O O O O O O O O OOO OOO O OOO O OOO OOO OOO A COMPREHENSIVE FILE OF INFORMATION GENERATED BY LIFE EXPERIMENTERS
LIFEFILE this issue concerns the scope of Thompson's codex system for known Life objects. Essentially, this includes Class V history information (age and final census) for all the smaller objects (six or less bits and also the heptominoes) which now includes about 8,000 different configurations! This will be presented in two sections.
Section One tabulates the number of objects of a particular size, structure, and symmetry that evolve into a specific stable object/constellation of Class I, Class II, or Class III (i.e. block, blinker or glider/R-pentomino census). The three-character code used to identify the original object set is defined as follows:
| Size | Structure | Symmetry |
|---|---|---|
| 3 | o (n orthogonally connected bits) | 4 (two-way orthog. and diag. and rotat.) |
| 4 | k (n kingwise connected bits) | 2 (two-way orthog. or diag. or rotat.) |
| 5 | d (n diagonal connected bits) | 1 (one-way orthog. or diag. or rotat.) |
| 6 | s (n spatially 〃) | 0 (none) |
Section Two tabulates by size, the distribution of age for objects that are 'mortal' (i.e. Class V.A) and 'immortal' (Classes V.B, V.C, and V.D).
Page 10
-- missing --
Page 11
symmetry evolving into specific stable objects/constellations of Class I,II,or III
Class II
1 a: blinker a: 8 blocks, g: 2 blocks,
* 1 boat, 1 boat,
* b: traffic light 4 beehives, 1 beehive,
* 1 ship, 3/4 t.lite,
* c: 6 blocks, 1 blinker 1 loaf, 1 glider.
* 4 blinkers,
* d: toad 6 gliders. h: 3 blocks,
1 1 boat,
* e: 2 blinkers (far) b: glider-α 1 beehive,
* 1 ship,
* 1 f: 3 blocks, 2 blinkers c: glider-β 2 gliders.
* *
* 1 g: beacon d: 3 blocks, i: 3 blocks,
* * 1 ship, 1 tub,
* * h: clock 2 gliders. 1 boat,
* * 1 beehive,
* * i: 4 beehives, 2 t.lites e: 2 blocks, 1 pond,
* * 1 ship, 7 blinkers,
* * j: 3 blocks, 2 blinkers 2 gliders. 1+3/4 t.lites,
1 1 1 glider.
5 * k: 6 blocks, 1 loaf, f: 1 block,
6 3 3 blinkers, 1/2+3/4+1 t.lite. 1 glider. j: 5 blocks,
* 1 4 beehives,
* 1 l: 2 blocks, 2 t.lites 1 blinker,
* 1 1 glider.
1 m: 2 boats, 4 beehives, 4 blinkers 1
* 2 * k: 8 blocks,
* 3 1 n: 1 block, 1 blinker, 3/4 t.lites. 3 2 2 2 boats,
* * * * * * 2 beehives,
* * * o: pulsar * * * 1 ship,
* 1 * * * * 1 loaf,
* * * p: 2 blinkers (close). * * * 1 fleet,
* * * * * * 1 blinker,
* * * * * * 2 gliders.
6 7 1 * * *
31 24 * 5 * 3
37 41 2 9 2 5
* * * * * *
* 1 2 1 * * *
* * * * 1 1 1 * *
* 1 * * * * 1 * * *
1 4 2 * * * 3 1 * * *
18 32 17 3 * 8 1 * 3 1 1 2 16 2 3 4 1 10 1 4
* * * * * * * * * * * * * * * * * * * *
* * * 2 * * 1 * * * * * * * * * * * * *
1 * * * * * * * * * * * * * * 1 * * * *
* * * * * * 1 * * * * * * * * * * * * *
5 26 13 7 * * 2 * * * * * 2 * * * * * * * *
261367 41 22 * 19 1 * 4 * * * 1 1 179 25 79 8 1 5 2 4 3 2 6
286431 75 35 1 28 10 1 7 1 1 2 3 1 196 27 82 13 2 15 3 8 3 2 6
* * * * * * * * * * * * * * * * * * * * * * * * *
* 1 3 * * * * * * * * 1 * * 1 1 * * * * * * * * * * *
3 4 3 * * 1 * * * * * * * * * * 1 * 3 2 1 * * 2 1 1 *
3 5 6 * * 1 * * * * * 1 * * 1 1 1 * 3 2 1 * * 2 1 1 *
a b c d e f g h i j k l m n o p a b c d e f g h i j k
Page 12
LIFEFILE Section Two - Distribution of longevity for all combinations
of six or less bits and also the heptominoes.
AGE Mortal objects (Class V.A) Immortal objects (Classes V.B-D)
3-bit 4-bit 5-bit 6-bit 7-bit 3-bit 4-bit 5-bit 6-bit 7-bit
0 - - - - - 1 2 3 9 *
1 * * * 3 * 1 10 59 184 1
2 8 36 138 833 4 12 47 603 6
3 5 145 1056 3 2 39 483 4
4 * 31 555 6 4 53 353 8
5 4 80 638 4 * 9 268 6
6 9 392 2 * 3 64 4
7 * 124 4 * 2 26 2
8 15 204 * * * 19 3
9 63 2 1 8 101 *
10 59 2 1 11 119 2
11 5 1 10 75 1
12 4 3 86 *
13 2 * 20 2
14 4 * 13 2
15 9 * * 2
16 16 * 12 1
17 8 * 8 1
18 * * 22 4
19 * * 37 4
20 * * 36 *
21 * * 17 *
22 * * 10 *
23 * * * 1
24 * * 5 *
25 * * 3 *
26 * * 4 *
27 * * 7 *
28 * * 4 *
32 * * * 1
34 * * 1 2
36 * * * 1
40 * * 1 *
45 1 * * *
46 8 * * *
69 * 118 4
76 NOTE: * * 4
109 Ages greater than fifty generations (Me- * 15 *
116 thuselahs) represent the maximum age for * 28 1
129 the minimum |AGE 5-bit 6-bit 7-bit| * 2 1
151 predecessor |1101 * 8 * | * 13 2
166 to a specific |1102 * 1 * | * 1 *
175 constellation. |1103 1 38 * | 2 75 6
178 There is actu- |1104 5 70 * | * 2 1
201 ally a small |1105 3 52 * | * 1 *
244 distribution |1106 22 * | * 3 *
248 about each of |1107 1 * | * 8 2
313 these values |1108 4 1 | * 3 *
365 as indicated |-----------------------| * 2 1
389 here for the |Total 9 196 1 | * 7 *
438 R-pentomino as a specific example. * 3 1
556 * 6 *
608 * 1 *
1105 9 196 1
Total 8 45 418 3984 27 2 33 258 3074 81
Page Scans
 Page 1
Page 1 Page 2
Page 2 Page 3
Page 3 Page 4
Page 4 Page 5
Page 5 Page 6
Page 6 Page 7
Page 7 Page 8
Page 8 Page 9
Page 9 Page 10
Page 10 Page 11
Page 11 Page 12
Page 12