Hebesphenomegacorona
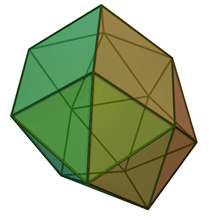
In geometry, the hebesphenomegacorona is one of the Johnson solids (J89). It is one of the elementary Johnson solids that do not arise from "cut and paste" manipulations of the Platonic and Archimedean solids. It has 21 faces, 18 triangles and 3 squares, 33 edges, and 14 vertices.
| Hebesphenomegacorona | |
|---|---|
 | |
| Type | Johnson J88 - J89 - J90 |
| Faces | 3x2+3x4 triangles 1+2 squares |
| Edges | 33 |
| Vertices | 14 |
| Vertex configuration | 4(32.42) 2+2x2(35) 4(34.4) |
| Symmetry group | C2v |
| Dual polyhedron | - |
| Properties | convex |
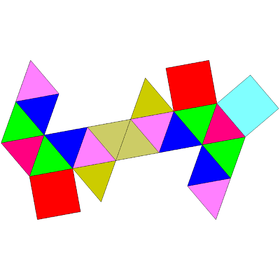
| Net | |
 | |

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]
Johnson uses the prefix hebespheno- to refer to a blunt wedge-like complex formed by three adjacent lunes, a lune being a square with equilateral triangles attached on opposite sides. Likewise, the suffix -megacorona refers to a crownlike complex of 12 triangles. Joining both complexes together results in the hebesphenomegacorona.[1]
The icosahedron can be obtained from the hebesphenomegacorona by merging the middle of the three squares into an edge, turning the neighboring two squares into triangles.
Cartesian Coordinates
Let a ≈ 0.21684 be the second smallest positive root of the polynomial
Then, Cartesian coordinates of a Hebesphenomegacorona with edge length 2 are given by the union of the orbits of the points
under the action of the group generated by reflections about the xz-plane and the yz-plane.[2]
References
- Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
- Timofeenko, A. V. (2009-10-17). "The non-platonic and non-Archimedean noncomposite polyhedra". Journal of Mathematical Sciences. 162 (5): 710–729. doi:10.1007/s10958-009-9655-0. ISSN 1072-3374.