Square cupola

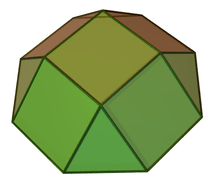
In geometry, the square cupola, sometimes called lesser dome, is one of the Johnson solids (J₄). It can be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagon.

Square cupola
Type	Johnson J3 - J4 - J5
Faces	4 triangles 1+4 squares 1 octagon
Edges	20
Vertices	12
Vertex configuration	8(3.4.8) 4(3.4^3)
Symmetry group	C4v, [4], (*44)
Rotation group	C4, [4]^+, (44)
Dual polyhedron	-
Properties	convex
Net

3D model of a square cupola

A Johnson solid is one of 92 strictly convex polyhedra that is composed of regular polygon faces but are not uniform polyhedra (that is, they are not Platonic solids, Archimedean solids, prisms, or antiprisms). They were named by Norman Johnson, who first listed these polyhedra in 1966.[1]

Formulae

The following formulae for the circumradius, surface area, volume, and height can be used if all faces are regular, with edge length a:

${\displaystyle C=\left({\frac {1}{2}}{\sqrt {5+2{\sqrt {2}}}}\right)a\approx 1.39897a,}$[2]

${\displaystyle A=(7+2{\sqrt {2}}+{\sqrt {3}})a^{2}\approx 11.56048a^{2},}$[3]

${\displaystyle V=\left(1+{\frac {2{\sqrt {2}}}{3}}\right)a^{3}\approx 1.94281a^{3}.}$[4]

${\displaystyle h={\frac {\sqrt {2}}{2}}a\approx 0.70711a}$[5]

Related polyhedra and honeycombs

Other convex cupolae

Family of convex cupolae

n	2	3	4	5	6
Name	{2} || t{2}	{3} || t{3}	{4} || t{4}	{5} || t{5}	{6} || t{6}
Cupola	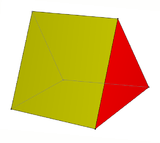Digonal cupola	Triangular cupola	Square cupola	Pentagonal cupola	Hexagonal cupola (Flat)
Related uniform polyhedra	Triangular prism	Cubocta- hedron	Rhombi- cubocta- hedron	Rhomb- icosidodeca- hedron	Rhombi- trihexagonal tiling

Dual polyhedron

The dual of the square cupola has 8 triangular and 4 kite faces:

Dual square cupola	Net of dual	3D model

Crossed square cupola

3D model of a crossed square cupola

The crossed square cupola is one of the nonconvex Johnson solid isomorphs, being topologically identical to the convex square cupola. It can be obtained as a slice of the nonconvex great rhombicuboctahedron or quasirhombicuboctahedron, analogously to how the square cupola may be obtained as a slice of the rhombicuboctahedron. As in all cupolae, the base polygon has twice as many edges and vertices as the top; in this case the base polygon is an octagram.

It may be seen as a cupola with a retrograde square base, so that the squares and triangles connect across the bases in the opposite way to the square cupola, hence intersecting each other.

Honeycombs

The square cupola is a component of several nonuniform space-filling lattices:

• with tetrahedra;
• with cubes and cuboctahedra; and
• with tetrahedra, square pyramids and various combinations of cubes, elongated square pyramids and elongated square bipyramids.[6]

References

1. Johnson, Norman W. (1966), "Convex polyhedra with regular faces", Canadian Journal of Mathematics, 18: 169–200, doi:10.4153/cjm-1966-021-8, MR 0185507, Zbl 0132.14603.
2. Wolfram Research, Inc. (2020). "Wolfram|Alpha Knowledgebase". Champaign, IL. PolyhedronData[{"Johnson", 4}, "Circumradius"] Cite journal requires |journal= (help)
3. Wolfram Research, Inc. (2020). "Wolfram|Alpha Knowledgebase". Champaign, IL. PolyhedronData[{"Johnson", 4}, "SurfaceArea"] Cite journal requires |journal= (help)
4. Wolfram Research, Inc. (2020). "Wolfram|Alpha Knowledgebase". Champaign, IL. PolyhedronData[{"Johnson", 4}, "Volume"] Cite journal requires |journal= (help)
5. Sapiña, R. "Area and volume of the Johnson solid J₄". Problemas y ecuaciones (in Spanish). ISSN 2659-9899. Retrieved 2020-07-16.
6. http://woodenpolyhedra.web.fc2.com/J4.html

External links

• Eric W. Weisstein, Square cupola (Johnson solid) at MathWorld.