Polydivisible number

In mathematics a polydivisible number (or magic number) is a number in a given number base with digits abcde... that has the following properties :

1. Its first digit a is not 0.
2. The number formed by its first two digits ab is a multiple of 2.
3. The number formed by its first three digits abc is a multiple of 3.
4. The number formed by its first four digits abcd is a multiple of 4.
5. etc.[1]

Definition

Let ${\displaystyle n}$ be a natural number, and let ${\displaystyle k=\lfloor \log _{b}{n}\rfloor +1}$ be the number of digits in the number in base ${\displaystyle b}$. ${\displaystyle n}$ is a polydivisible number if for all ${\displaystyle 0\leq i<k}$,

${\displaystyle {\frac {n-(n{\bmod {b}}^{k-i-1})}{b^{k-i-1}}}\equiv 0{\bmod {i}}}$.

For example, 10801 is a seven-digit polydivisible number in base 4, as

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-0-1})}{4^{7-0-1}}}={\frac {10801-(10801{\bmod {4}}^{6})}{4^{6}}}={\frac {10801-(10801{\bmod {4}}096)}{4096}}={\frac {10801-2609}{4096}}={\frac {8192}{4096}}=2\equiv 0{\bmod {1}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-1-1})}{4^{7-1-1}}}={\frac {10801-(10801{\bmod {4}}^{5})}{4^{5}}}={\frac {10801-(10801{\bmod {1}}024)}{1024}}={\frac {10801-561}{1024}}={\frac {10240}{1024}}=10\equiv 0{\bmod {2}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-2-1})}{4^{7-2-1}}}={\frac {10801-(10801{\bmod {4}}^{4})}{4^{4}}}={\frac {10801-(10801{\bmod {2}}56)}{256}}={\frac {10801-49}{256}}={\frac {10752}{256}}=42\equiv 0{\bmod {3}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-3-1})}{4^{7-3-1}}}={\frac {10801-(10801{\bmod {4}}^{3})}{4^{3}}}={\frac {10801-(10801{\bmod {6}}4)}{64}}={\frac {10801-49}{64}}={\frac {10752}{64}}=168\equiv 0{\bmod {4}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-4-1})}{4^{7-4-1}}}={\frac {10801-(10801{\bmod {4}}^{2})}{4^{2}}}={\frac {10801-(10801{\bmod {1}}6)}{16}}={\frac {10801-1}{16}}={\frac {10800}{16}}=675\equiv 0{\bmod {5}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-5-1})}{4^{7-5-1}}}={\frac {10801-(10801{\bmod {4}}^{1})}{4^{1}}}={\frac {10801-(10801{\bmod {4}})}{4}}={\frac {10801-1}{4}}={\frac {10800}{4}}=2700\equiv 0{\bmod {6}}}$

${\displaystyle {\frac {10801-(10801{\bmod {4}}^{7-6-1})}{4^{7-6-1}}}={\frac {10801-(10801{\bmod {4}}^{0})}{4^{0}}}={\frac {10801-(10801{\bmod {1}})}{1}}={\frac {10801-0}{1}}={\frac {10801}{1}}=10801\equiv 0{\bmod {7}}}$

Enumeration

For any given base ${\displaystyle b}$, there are only a finite number of polydivisible numbers.

Maximum polydivisible number

All numbers are represented in base ${\displaystyle b}$, using A−Z to represent digit values 10 to 35.

Base ${\displaystyle b}$	Maximum polydivisible number	Number of digits in maximum polydivisible number
2	10	2
3	20 0220	6
4	222 0301	7
5	40220 42200	10
10	36085 28850 36840 07860 36725[2][3][4]	25[2][3][4]
12	6068 903468 50BA68 00B036 206464	28

Estimate for ${\displaystyle F_{b}(n)}$ and ${\displaystyle \Sigma (b)}$

Graph of number of ${\displaystyle n}$-digit polydivisible numbers in base 10 ${\displaystyle F_{10}(n)}$ vs estimate of ${\displaystyle F_{10}(n)}$

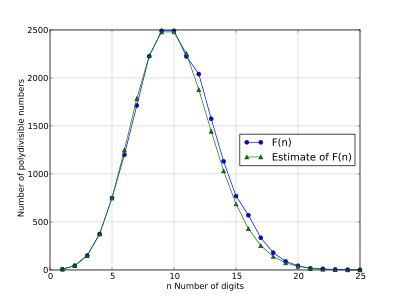
Let ${\displaystyle n}$ be the number of digits. The function ${\displaystyle F_{b}(n)}$ determines the number of polydivisible numbers that has ${\displaystyle n}$ digits in base ${\displaystyle b}$, and the function ${\displaystyle \Sigma (b)}$ is the total number of polydivisible numbers in base ${\displaystyle b}$.

If ${\displaystyle k}$ is a polydivisible number in base ${\displaystyle b}$ with ${\displaystyle n-1}$ digits, then it can be extended to create a polydivisible number with ${\displaystyle n}$ digits if there is a number between ${\displaystyle bk}$ and ${\displaystyle b(k+1)-1}$ that is divisible by ${\displaystyle n}$. If ${\displaystyle n}$ is less or equal to ${\displaystyle b}$, then it is always possible to extend an ${\displaystyle n-1}$ digit polydivisible number to an ${\displaystyle n}$-digit polydivisible number in this way, and indeed there may be more than one possible extension. If ${\displaystyle n}$ is greater than ${\displaystyle b}$, it is not always possible to extend a polydivisible number in this way, and as ${\displaystyle n}$ becomes larger, the chances of being able to extend a given polydivisible number become smaller. On average, each polydivisible number with ${\displaystyle n-1}$ digits can be extended to a polydivisible number with ${\displaystyle n}$ digits in ${\displaystyle {\frac {b}{n}}}$ different ways. This leads to the following estimate for ${\displaystyle F_{b}(n)}$ :

${\displaystyle F_{b}(n)\approx (b-1){\frac {b^{n-1}}{n!}}.}$

Summing over all values of n, this estimate suggests that the total number of polydivisible numbers will be approximately

${\displaystyle \Sigma (b)\approx {\frac {b-1}{b}}(e^{b}-1)}$

Base ${\displaystyle b}$	${\displaystyle \Sigma (b)}$	Est. of ${\displaystyle \Sigma (b)}$	Percent Error
2	2	${\displaystyle {\frac {1}{2}}(e^{2}-1)\approx 3.1945}$	59.7%
3	15	${\displaystyle {\frac {2}{3}}(e^{3}-1)\approx 12.725}$	-15.1%
4	37	${\displaystyle {\frac {3}{4}}(e^{4}-1)\approx 40.199}$	8.64%
5	127	${\displaystyle {\frac {4}{5}}(e^{5}-1)\approx 117.93}$	−7.14%
10	20456[2]	${\displaystyle {\frac {9}{10}}(e^{10}-1)\approx 19823}$	-3.09%

Specific bases

All numbers are represented in base ${\displaystyle b}$, using A−Z to represent digit values 10 to 35.

Base 2

Length n	F2(n)	Est. of F2(n)	Polydivisible numbers
1	1	1	1
2	1	1	10

Base 3

Length n	F3(n)	Est. of F3(n)	Polydivisible numbers
1	2	2	1, 2
2	3	3	11, 20, 22
3	3	3	110, 200, 220
4	3	2	1100, 2002, 2200
5	2	1	11002, 20022
6	2	1	110020, 200220
7	0	0	${\displaystyle \varnothing }$

Base 4

Length n	F4(n)	Est. of F4(n)	Polydivisible numbers
1	3	3	1, 2, 3
2	6	6	10, 12, 20, 22, 30, 32
3	8	8	102, 120, 123, 201, 222, 300, 303, 321
4	8	8	1020, 1200, 1230, 2010, 2220, 3000, 3030, 3210
5	7	6	10202, 12001, 12303, 20102, 22203, 30002, 32103
6	4	4	120012, 123030, 222030, 321030
7	1	2	2220301
8	0	1	${\displaystyle \varnothing }$

Base 5

The polydivisible numbers in base 5 are

1, 2, 3, 4, 11, 13, 20, 22, 24, 31, 33, 40, 42, 44, 110, 113, 132, 201, 204, 220, 223, 242, 311, 314, 330, 333, 402, 421, 424, 440, 443, 1102, 1133, 1322, 2011, 2042, 2200, 2204, 2231, 2420, 2424, 3113, 3140, 3144, 3302, 3333, 4022, 4211, 4242, 4400, 4404, 4431, 11020, 11330, 13220, 20110, 20420, 22000, 22040, 22310, 24200, 24240, 31130, 31400, 31440, 33020, 33330, 40220, 42110, 42420, 44000, 44040, 44310, 110204, 113300, 132204, 201102, 204204, 220000, 220402, 223102, 242000, 242402, 311300, 314000, 314402, 330204, 333300, 402204, 421102, 424204, 440000, 440402, 443102, 1133000, 1322043, 2011021, 2042040, 2204020, 2420003, 2424024, 3113002, 3140000, 3144021, 4022042, 4211020, 4431024, 11330000, 13220431, 20110211, 20420404, 24200031, 31400004, 31440211, 40220422, 42110202, 44310242, 132204314, 201102110, 242000311, 314000044, 402204220, 443102421, 1322043140, 2011021100, 3140000440, 4022042200

The smallest base 5 polydivisible numbers with n digits are

1, 11, 110, 1102, 11020, 110204, 1133000, 11330000, 132204314, 1322043140, 0, 0, 0...

The largest base 5 polydivisible numbers with n digits are

4, 44, 443, 4431, 44310, 443102, 4431024, 44310242, 443102421, 4022042200, 0, 0, 0...

The number of base 5 polydivisible numbers with n digits are

4, 10, 17, 21, 21, 21, 13, 10, 6, 4, 0, 0, 0...

Length n	F5(n)	Est. of F5(n)
1	4	4
2	10	10
3	17	17
4	21	21
5	21	21
6	21	17
7	13	12
8	10	8
9	6	4
10	4	2

Base 10

The polydivisible numbers in base 10 are

1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 12, 14, 16, 18, 20, 22, 24, 26, 28, 30, 32, 34, 36, 38, 40, 42, 44, 46, 48, 50, 52, 54, 56, 58, 60, 62, 64, 66, 68, 70, 72, 74, 76, 78, 80, 82, 84, 86, 88, 90, 92, 94, 96, 98, 102, 105, 108, 120, 123, 126, 129, 141, 144, 147, 162, 165, 168, 180, 183, 186, 189, ... (sequence A144688 in the OEIS)

The smallest base 10 polydivisible numbers with n digits are

1, 10, 102, 1020, 10200, 102000, 1020005, 10200056, 102000564, 1020005640, 10200056405, 102006162060, 1020061620604, 10200616206046, 102006162060465, 1020061620604656, 10200616206046568, 108054801036000018, 1080548010360000180, 10805480103600001800, ... (sequence A214437 in the OEIS)

The largest base 10 polydivisible numbers with n digits are

9, 98, 987, 9876, 98765, 987654, 9876545, 98765456, 987654564, 9876545640, 98765456405, 987606963096, 9876069630960, 98760696309604, 987606963096045, 9876062430364208, 98485872309636009, 984450645096105672, 9812523240364656789, 96685896604836004260, ... (sequence A225608 in the OEIS)

The number of base 10 polydivisible numbers with n digits are

9, 45, 150, 375, 750, 1200, 1713, 2227, 2492, 2492, 2225, 2041, 1575, 1132, 770, 571, 335, 180, 90, 44, 18, 12, 6, 3, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, ... (sequence A143671 in the OEIS)

Length n	F10(n)[5]	Est. of F10(n)
1	9	9
2	45	45
3	150	150
4	375	375
5	750	750
6	1200	1250
7	1713	1786
8	2227	2232
9	2492	2480
10	2492	2480

Length n	F10(n) [5]	Est. of F10(n)
11	2225	2255
12	2041	1879
13	1575	1445
14	1132	1032
15	770	688
16	571	430
17	335	253
18	180	141
19	90	74
20	44	37

Length n	F10(n) [5]	Est. of F10(n)
21	18	17
22	12	8
23	6	3
24	3	1
25	1	1

Programming example

The example below searches for polydivisible numbers in Python.

def find_polydivisible(base: int) -> List[int]:
    """Find polydivisible number."""
    numbers = []
    previous = []
    for i in range(1, base):
        previous.append(i)
    new = []
    digits = 2
    while not previous == []:
        numbers.append(previous)
        for i in range(0, len(previous)):
            for j in range(0, base):
                number = previous[i] * base + j
                if number % digits == 0:
                    new.append(number)
        previous = new
        new = []
        digits = digits + 1
    return numbers

Related problems

Polydivisible numbers represent a generalization of the following well-known[2] problem in recreational mathematics :

Arrange the digits 1 to 9 in order so that the first two digits form a multiple of 2, the first three digits form a multiple of 3, the first four digits form a multiple of 4 etc. and finally the entire number is a multiple of 9.

The solution to the problem is a nine-digit polydivisible number with the additional condition that it contains the digits 1 to 9 exactly once each. There are 2,492 nine-digit polydivisible numbers, but the only one that satisfies the additional condition is

381 654 729[6]

Other problems involving polydivisible numbers include:

• Finding polydivisible numbers with additional restrictions on the digits - for example, the longest polydivisible number that only uses even digits is

480 006 882 084 660 840 40

• Finding palindromic polydivisible numbers - for example, the longest palindromic polydivisible number is

300 006 000 03

• A common, trivial extension of the aforementioned example is to arrange the digits 0 to 9 to make a 10 digit number in the same way, the result is 3816547290. This is a pandigital polydivisible number.

References

1. De, Moloy, MATH’S BELIEVE IT OR NOT (PDF)
2. Parker, Matt (2014), "Can you digit?", Things to Make and Do in the Fourth Dimension, Particular Books, pp. 7–8 – via Google Books
3. Wells, David (1986), The Penguin Dictionary of Curious and Interesting Numbers, Penguin Books, p. 197 – via Google Books
4. Lines, Malcolm (1986), "How Do These Series End?", A Number for your Thoughts, Taylor and Francis Group, p. 90
5. (sequence A143671 in the OEIS)
6. Lanier, Susie, Nine Digit Number

External links

• YouTube - a pandigital number that is also polydivisible