Deficient number

In number theory, a deficient number or defective number is a number n for which the sum of divisors σ(n)<2n, or, equivalently, the sum of proper divisors (or aliquot sum) s(n)<n. The value 2n − σ(n) (or n − s(n)) is called the number's deficiency.

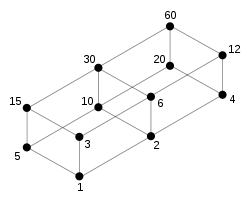
Demonstration, with Cuisenaire rods, of the deficiency of the number 8

Examples

The first few deficient numbers are:

1, 2, 3, 4, 5, 7, 8, 9, 10, 11, 13, 14, 15, 16, 17, 19, 21, 22, 23, 25, 26, 27, 29, 31, 32, 33, 34, 35, 37, 38, 39, 41, 43, 44, 45, 46, 47, 49, 50, ... (sequence A005100 in the OEIS)

As an example, consider the number 21. Its proper divisors are 1, 3 and 7, and their sum is 11. Because 11 is less than 21, the number 21 is deficient. Its deficiency is 2 × 21 − 32 = 10.

Properties
  • Since the aliquot sums of prime numbers equal 1, all prime numbers are deficient.
  • An infinite number of both even and odd deficient numbers exist.
  • All odd numbers with one or two distinct prime factors are deficient.
  • All proper divisors of deficient or perfect numbers are deficient.
  • There exists at least one deficient number in the interval for all sufficiently large n.[1]
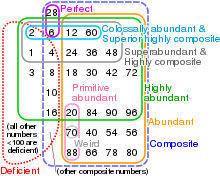
Euler diagram of abundant, primitive abundant, highly abundant, superabundant, colossally abundant, highly composite, superior highly composite, weird and perfect numbers under 100 in relation to deficient and composite numbers

Closely related to deficient numbers are perfect numbers with σ(n) = 2n, and abundant numbers with σ(n) > 2n. The natural numbers were first classified as either deficient, perfect or abundant by Nicomachus in his Introductio Arithmetica (circa 100 CE).

gollark: Have you SEEN printers, Moose.monster.23?
gollark: I mean, they're evil, yes, but handwriting things is very slow and bad.
gollark: Wait, why did you not just use a printer?
gollark: You forgot strange kek, charm kek, up kek and down kek!
gollark: What if we make it so that proposals are *automatically* passed when the rules state they should be, and directly patch the code of the bot?

See also

References
  1. Sándor et al (2006) p.108
  • Sándor, József; Mitrinović, Dragoslav S.; Crstici, Borislav, eds. (2006). Handbook of number theory I. Dordrecht: Springer-Verlag. ISBN 1-4020-4215-9. Zbl 1151.11300.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.