Motzkin number
In mathematics, the nth Motzkin number is the number of different ways of drawing non-intersecting chords between n points on a circle (not necessarily touching every point by a chord). The Motzkin numbers are named after Theodore Motzkin and have diverse applications in geometry, combinatorics and number theory.
The Motzkin numbers for form the sequence:
Examples
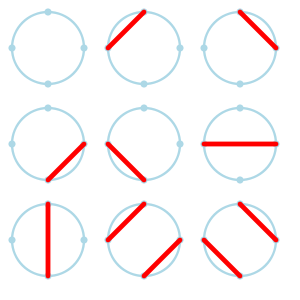
The following figure shows the 9 ways to draw non-intersecting chords between 4 points on a circle (M4 = 9):
The following figure shows the 21 ways to draw non-intersecting chords between 5 points on a circle (M5 = 21):
Properties
The Motzkin numbers satisfy the recurrence relations
The Motzkin numbers can be expressed in terms of binomial coefficients and Catalan numbers:
The generating series of the Motzkin numbers satisfies
- .
A Motzkin prime is a Motzkin number that is prime. As of October 2013, four such primes are known:
Combinatorial interpretations
The Motzkin number for n is also the number of positive integer sequences of length n − 1 in which the opening and ending elements are either 1 or 2, and the difference between any two consecutive elements is −1, 0 or 1. Equivalently, the Motzkin number for n is the number of positive integer sequences of length n + 1 in which the opening and ending elements are 1, and the difference between any two consecutive elements is −1, 0 or 1.
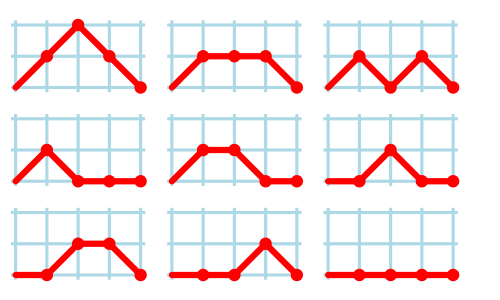
Also, the Motzkin number for n gives the number of routes on the upper right quadrant of a grid from coordinate (0, 0) to coordinate (n, 0) in n steps if one is allowed to move only to the right (up, down or straight) at each step but forbidden from dipping below the y = 0 axis.
For example, the following figure shows the 9 valid Motzkin paths from (0, 0) to (4, 0):
There are at least fourteen different manifestations of Motzkin numbers in different branches of mathematics, as enumerated by Donaghey & Shapiro (1977) in their survey of Motzkin numbers. Guibert, Pergola & Pinzani (2001) showed that vexillary involutions are enumerated by Motzkin numbers.
References
- Bernhart, Frank R. (1999), "Catalan, Motzkin, and Riordan numbers", Discrete Mathematics, 204 (1–3): 73–112, doi:10.1016/S0012-365X(99)00054-0
- Donaghey, R.; Shapiro, L. W. (1977), "Motzkin numbers", Journal of Combinatorial Theory, Series A, 23 (3): 291–301, doi:10.1016/0097-3165(77)90020-6, MR 0505544
- Guibert, O.; Pergola, E.; Pinzani, R. (2001), "Vexillary involutions are enumerated by Motzkin numbers", Annals of Combinatorics, 5 (2): 153–174, doi:10.1007/PL00001297, ISSN 0218-0006, MR 1904383
- Motzkin, T. S. (1948), "Relations between hypersurface cross ratios, and a combinatorial formula for partitions of a polygon, for permanent preponderance, and for non-associative products", Bulletin of the American Mathematical Society, 54 (4): 352–360, doi:10.1090/S0002-9904-1948-09002-4