Gömböc

The gömböc (Hungarian: [ˈɡømbøt͡s]) is a convex three-dimensional homogeneous body that when resting on a flat surface has just one stable and one unstable point of equilibrium. Its existence was conjectured by the Russian mathematician Vladimir Arnold in 1995 and proven in 2006 by the Hungarian scientists Gábor Domokos and Péter Várkonyi. The gömböc shape is not unique; it has countless varieties, most of which are very close to a sphere and all with a very strict shape tolerance (about one part in a thousand).

A mono-monostatic gömböc (defined in §History) returning to its stable equilibrium position
The mono-monostatic gömböc (defined in §History) in the stable equilibrium position
4.5 m (15 ft) gömböc statue in the Corvin Quarter in Budapest 2017

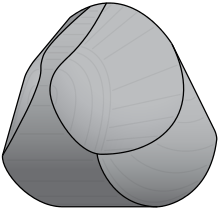
The most famous solution, capitalized as Gömböc to distinguish it from the generic gömböc, has a sharpened top, as shown in the photo. Its shape helped to explain the body structure of some tortoises in relation to their ability to return to equilibrium position after being placed upside down.[1][2][3][4] Copies of the gömböc have been donated to institutions and museums, and the largest one was presented at the World Expo 2010 in Shanghai in China.[5][6] In December 2017, a 4.5 m (15 ft) gömböc statue was installed in the Corvin Quarter (Corvin-negyed) in Budapest.[7]

Name

If analyzed quantitatively in terms of flatness and thickness, the discovered mono-monostatic body (defined in §History) is the most sphere-like, apart from the sphere itself. Because of this, it was named gömböc, a diminutive form of gömb ("sphere" in Hungarian). The word gömböc referred originally to a sausage-like food: seasoned pork filled in pig-stomach, similar to haggis. There is a Hungarian folk tale about an anthropomorphic gömböc that swallows several people whole.[8]

History
When a roly-poly toy is pushed, the height of the center of mass rises from the green line to the orange line, and the center of mass is no longer over the point of contact with the ground.

In geometry, a body with a single stable resting position is called monostatic, and the term mono-monostatic has been coined to describe a body which additionally has only one unstable point of balance. (The previously known monostatic polyhedron does not qualify, as it has three unstable equilibria.) A sphere weighted so that its center of mass is shifted from the geometrical center is a mono-monostatic body. A more common example is the Comeback Kid, Weeble or roly-poly toy (see left figure). Not only does it have a low center of mass, but it also has a specific shape. At equilibrium, the center of mass and the contact point are on the line perpendicular to the ground. When the toy is pushed, its center of mass rises and also shifts away from that line. This produces a righting moment which returns the toy to the equilibrium position.

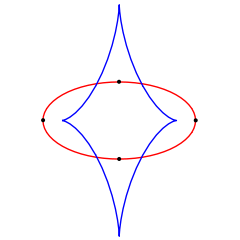
The above examples of mono-monostatic objects are necessarily inhomogeneous, that is, the density of their material varies across their body. The question of whether it is possible to construct a three-dimensional body which is mono-monostatic but also homogeneous and convex was raised by Russian mathematician Vladimir Arnold in 1995. The requirement of being convex is essential as it is trivial to construct a mono-monostatic non-convex body (an example would be a ball with a cavity inside it). Convex means that a straight line between any two points on a body lies inside the body, or, in other words, that the surface has no sunken regions but instead bulges outward (or is at least flat) at every point. It was already well known, from a geometrical and topological generalization of the classical four-vertex theorem, that a plane curve has at least four extrema of curvature, specifically, at least two local maxima and at least two local minima (see right figure), meaning that a (convex) mono-monostatic object does not exist in two dimensions. Whereas a common anticipation was that a three-dimensional body should also have at least four extrema, Arnold conjectured that this number could be smaller.[9]

Mathematical solution
An ellipse (red) and its evolute (blue), showing the four vertices of the curve. Each vertex corresponds to a cusp on the evolute.
The characteristic shape of the gömböc

The problem was solved in 2006 by Gábor Domokos and Péter Várkonyi. Domokos is an engineer and is the head of Mechanics, Materials and Structures at Budapest University of Technology and Economics. Since 2004, he has been the youngest member of the Hungarian Academy of Sciences. Várkonyi was trained as an architect; he was a student of Domokos and a silver medalist at the International Physics Olympiad in 1997. After staying as a postdoctoral researcher at Princeton University in 2006–2007, he assumed an assistant professor position at Budapest University of Technology and Economics.[9][10] Domokos had previously been working on mono-monostatic bodies. In 1995 he met Arnold at a major mathematics conference in Hamburg, where Arnold presented a plenary talk illustrating that most geometrical problems have four solutions or extremal points. In a personal discussion, however, Arnold questioned whether four is a requirement for mono-monostatic bodies and encouraged Domokos to seek examples with fewer equilibria.[11]

The rigorous proof of the solution can be found in references of their work.[9] The summary of the results is that the three-dimensional homogeneous convex (mono-monostatic) body, which has one stable and one unstable equilibrium point, does exist and is not unique. Such bodies are hard to visualize, describe or identify. Their form is dissimilar to any typical representative of any other equilibrium geometrical class. They should have minimal "flatness", and, to avoid having two unstable equilibria, must also have minimal "thinness". They are the only non-degenerate objects having simultaneously minimal flatness and thinness. The shape of those bodies is very sensitive to small variation, outside which it is no longer mono-monostatic. For example, the first solution of Domokos and Várkonyi closely resembled a sphere, with a shape deviation of only 10−5. It was dismissed, as it was extremely hard to test experimentally.[12] Their published solution was less sensitive; yet it has a shape tolerance of 10−3, that is 0.1 mm for a 10 cm size.[13]

Domokos and his wife developed a classification system for shapes based on their points of equilibrium by analyzing pebbles and noting their equilibrium points.[14] In one experiment, they tried 2,000 pebbles collected on the beaches of the Greek island of Rhodes and found not a single mono-monostatic body among them, illustrating the difficulty of finding or constructing such a body.[9][12]

The solution of Domokos and Várkonyi has curved edges and resembles a sphere with a squashed top. In the top figure, it rests in its stable equilibrium. Its unstable equilibrium position is obtained by rotating the figure 180° about a horizontal axis. Theoretically, it will rest there, but the smallest perturbation will bring it back to the stable point. The mathematical gömböc has sphere-like properties. In particular, its flatness and thinness are minimal, and this is the only type of nondegenerate object with this property.[9] Domokos and Várkonyi are interested to find a polyhedral solution with the surface consisting of a minimal number of flat planes. Therefore, they offer a prize to anyone who finds such solution, which amounts to $10,000 divided by the number of planes in the solution. Obviously, one can approximate a curvilinear gömböc with a finite number of discrete surfaces; however, their estimate is that it would take thousands of planes to achieve that. They hope, by offering this prize, to stimulate finding a radically different solution from their own.[4]

Relation to animals
The shape of the Indian star tortoise resembles a gömböc. This tortoise rolls easily without relying much on its limbs.

The balancing properties of the gömböc are associated with the "righting response" ⁠— the ability to turn back when placed upside down⁠ ⁠— of shelled animals such as tortoises and beetles. This may happen in a fight or predator attack and is crucial for their survival. The presence of only one stable and unstable point in a gömböc means that it would return to one equilibrium position no matter how it is pushed or turned around. Whereas relatively flat animals (such as beetles) heavily rely on momentum and thrust developed by moving their limbs and wings, the limbs of many dome-shaped tortoises are too short to be of use in righting themselves.

Domokos and Várkonyi spent a year measuring tortoises in the Budapest Zoo, Hungarian Museum of Natural History and various pet shops in Budapest, digitizing and analyzing their shells, and attempting to "explain" their body shapes and functions from their geometry work. Their first biology paper was rejected five times, but finally accepted by the biology journal Proceedings of the Royal Society. It was then immediately popularized in several science news reports, including those of the most prestigious science journals Nature[3] and Science.[4][15] The reported model can be summarized as flat shells in tortoises are advantageous for swimming and digging. However, the sharp shell edges hinder the rolling. Those tortoises usually have long legs and neck and actively use them to push the ground, in order to return to the normal position if placed upside down. On the contrary, "rounder" tortoises easily roll on their own; those have shorter limbs and use them little when recovering lost balance. (Some limb movement would always be needed because of imperfect shell shape, ground conditions, etc.) Round shells also resist better the crushing jaws of a predator and are better for thermal regulation.[1][2][3][4]

The Argentine snake-necked turtle is an example of a flat turtle, which relies on its long neck and legs to turn over when placed upside down.

The explanation of tortoise body shape, using the gömböc theory, has already been accepted by some biologists. For example, Robert McNeill Alexander, one of the pioneers of modern biomechanics, used it in his plenary lecture on optimization in evolution in 2008.[16]

Relation to rocks, pebbles and Plato's cube

The gömböc has motivated research about the evolution of natural shapes: while gömböc-shaped pebbles are rare, the connection between geometric shape and the number of static balance points appears to be a key to understand natural shape evolution:[17] both experimental and numerical evidence indicates that the number N of static equilibrium points of sedimentary particles is being reduced in natural abrasion. This observation helped to identify the geometric partial differential equations governing this process and these models provided key evidence not only on the provenance of Martian pebbles,[18] but also on the shape of the interstellar asteroid ʻOumuamua.[19]

Although both chipping by collisions and frictional abrasion gradually eliminates balance points, still, shapes stop short of becoming a Gömböc; the latter, having N=2 balance points, appears as an unattainable end point of this natural process. The likewise invisible starting point appears to be the cube with N=26 balance points, confirming a postulate by Plato who identified the four classical elements and the cosmos with the five Platonic solids, in particular, he identified the element Earth with the cube. While this claim has been viewed for a long time only as a metaphor, recent research [20] proved that it is qualitatively correct: the most generic fragmentation patterns in nature produce fragments which can be approximated by polyhedra and the respective statistical averages for the numbers of faces, vertices, and edges are 6, 8, and 12, respectively, agreeing with the corresponding values of the cube. This is well reflected in the allegory of the cave, where Plato explains that the immediately visible physical world (in the current example, the shape of individual natural fragments) may only be a distorted shadow of the true essence of the phenomenon, an idea (in the current example, the cube).

Engineering applications

Due to their vicinity to the sphere, all mono-monostatic shapes have very small tolerance for imperfections and even for the physical gömböc design this tolerance is daunting (<0.01%). Nevertheless, if we drop the requirement of homogeneity, the gömböc design serves as a good starting geometry if we want to find the optimal shape for self-righting objects carrying bottom weights. This inspired engineers[21] designing gömböc-like cages for drones exposed to mid-air collisions. A team from MIT and Harvard proposed[22] a Gömböc-inspired capsule that releases insulin in the stomach and could replace injections for patients with type-1 diabetes. The key element of the new capsule is its ability to find a unique position in the stomach, and this ability is based on its bottom weight and its overall geometry, optimized for self-righting. According to the article, after studying the papers on the gömböc[9] and the geometry of turtles,[1] the authors ran an optimization, which produced a mono-monostatic capsule with a contour almost identical to the frontal view of the gömböc.

Production

The strict shape tolerance of gömböcs hindered production. The first prototype of a gömböc was manufactured in summer 2006 using three-dimensional rapid prototyping technology. Its accuracy, however, was below requirements, and the gömböc would often get stuck in an intermediate position rather than returning to the stable equilibrium. The technology was improved by using numerical control milling to increase the spatial accuracy to the required level and to use various construction materials. In particular, transparent (especially lightly colored) solids are visually appealing, as they demonstrate the homogeneous composition. Current materials for gömböcs include various metals and alloys, plastics such as Plexiglass. Beyond computer-controlled milling, a special hybrid technology (using milling and molding) has been developed to produce functional but light and more affordable gömböc models.[23] The balancing properties of a gömböc are affected by mechanical defects and dust both on its body and on the surface on which it rests. If damaged, the process of restoring the original shape is more complex than producing a new one.[24] Although in theory the balancing properties should not depend on the material and object size, in practice, both larger and heavier gömböcs have better chances to return to equilibrium in case of defects.[25]

Individual gömböc models

In 2007, a series of individual gömböc models has been launched. These models carry a unique number N in the range 1 ≤ N ≤ Y where Y denotes the current year. Each number is produced only once, however, the order of production is not according to N, rather, at request. Initially these models were produced by rapid prototyping, with the serial number appearing inside, printed with a different material having the same density. Now all individual models are made by Numerical control (CNC) machining and the production process of each individual gömböc model includes the manufacturing of individual tools which are subsequently discarded. The first individually numbered Gömböc model (Gömböc 001) was presented by Domokos and Várkonyi as a gift to Vladimir Arnold on occasion of his 70th birthday.[26] and Professor Arnold later donated this piece to the Steklov Institute of Mathematics where it is on exhibit. While the majority of the existing numbered pieces are owned by private individuals, many pieces are public at renowned institutions worldwide.

There are two types of gömböc models which do not carry a serial number. Eleven pieces were manufactured for the World Expo 2010, and the logo of the Hungarian Pavilion was engraved into these pieces. The other non-numbered type of individual gömböc models are the insignia of the Stephen Smale Prize in Mathematics, awarded by the Foundations of Computational Mathematics every third year.

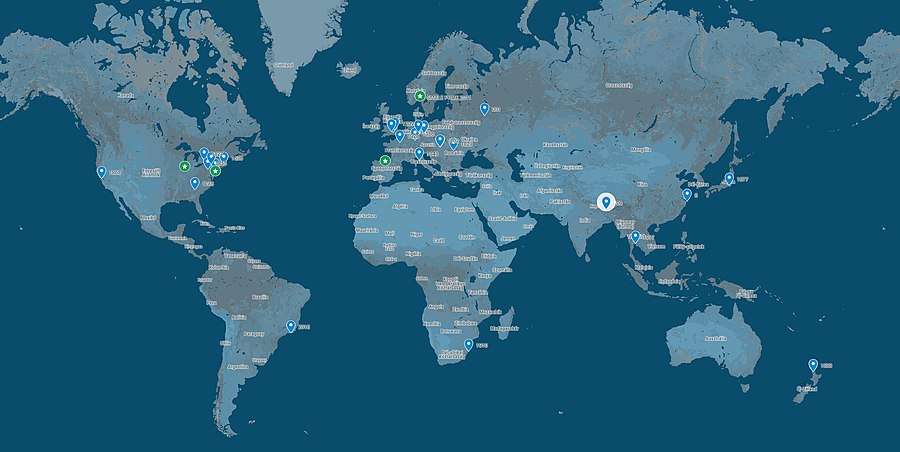
For more information on individual Gömböc pieces see the table below, click on the interactive version of the accompanying map or see the online booklet.[27]

This is a map showing individual gömböc models around the world. By clicking this link you can view the interactive version of this map.
Serial numberInstitutionLocationNumber's explanationDate of exhibitTechnologyMaterialHeight (mm)Link to more detailOther comments
1Steklov Institute of Mathematics Moscow, RussiaFirst-ever numbered gömböcAug 2007Rapid prototypingPlastic85Picture of exhibitGift of Vladimir Arnold
8Hungarian Pavilion Dinghai, ChinaThe number 8 is considered as a lucky number in Chinese numerologyDec 2017assembled from CNC-made partsPlexiglass500Picture of exhibit View of pavilionFirst on exhibit at the World Expo 2010
13Windsor Castle Windsor, Berkshire, United KingdomFeb 2017CNC99.99% certified silver90Picture of exhibitSponsored by Ottó Albrecht
108Residence of the Shamarpa Kalimpong, IndiaThe number of volumes of the Kangyur, containing the teachings of BuddhaFeb 2008CNCAlMgSi alloy90Pictures of the event of donation Gift of the Kamala Buddhist Community
400New College, Oxford Oxford, United KingdomAnniversary of the foundation of the chair for the Savilian Professor of GeometryNov 2019CNCBronze90Picture of exhibitSponsored by Ottó Albrecht
1209University of Cambridge Cambridge, United KingdomYear of foundationJan 2009CNCAlMgSi alloy90News on the Whipple Museum's websiteGift of the inventors
1343University of Pisa Pisa, ItalyYear of foundationApr 2019CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1348Windsor Castle Windsor, Berkshire, United KingdomYear of foundation of the Order of the GarterFeb 2017CNCClear plexiglass180Picture of ceremonySponsored by Ottó Albrecht
1386University of Heidelberg Heidelberg, GermanyYear of foundationJul 2019CNCClear plexiglass180Picture of exhibitSponsored by Ottó Albrecht
1409Leipzig University Leipzig, GermanyYear of foundationDec 2014CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1546Trinity College, Cambridge Cambridge, United KingdomYear of foundationDec 2008CNCAlMgSi alloy90Picture of exhibitGift of Domokos
1636Harvard University Boston, Massachusetts, United StatesYear of foundationJun 2019CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Model Collection
1737University of Göttingen Göttingen, GermanyYear of foundationOct 2012CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Model Collection
1746Princeton University Princeton, New Jersey, United StatesYear of foundationJul 2016CNCClear plexiglass180Picture of exhibitSponsored by Ottó Albrecht
1785University of Georgia Athens, Georgia, United StatesYear of foundationJan 2017CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1802Hungarian National Museum Budapest, HungaryYear of foundationMar 2012CNCClear plexiglass195Picture of exhibitSponsored by Thomas Cholnoky
1821E.ON Climate and Renewables London, United KingdomYear of invention of the electric motor by Michael FaradayMay 2012CNCAlMgSi alloy90Picture of ceremonyEnvironmental Safety Award
1823Bolyai Museum, Teleki Library Târgu Mureș, RomaniaYear of the Temesvár Letter by János Bolyai when he announced his discovery of non-Euclidean geometryOct 2012CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1825Hungarian Academy of Sciences Budapest, HungaryYear of foundationOct 2009CNCAlMgSi alloy180Picture of exhibitOn exhibit in the Academy's main building
1827University of Toronto Toronto, Ontario, CanadaYear of foundationJun 2019CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Collection. Sponsored by Ottó Albrecht
1828Technical University of Dresden Dresden, Saxony, GermanyYear of foundationJun 2020CNCAlMgSi alloy90Picture of exhibitPart of the Digital Archive of Mathematical Models (DAMM) . Sponsored by Ottó Albrecht
1837National and Kapodistrian University of Athens Athens, GreeceYear of foundationDec 2019CNCAlMgSi alloy90Picture of exhibitGift of the Hungarian Embassy
1855Pennsylvania State University College Park, Pennsylvania, United StatesYear of foundationSep 2015CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1865Cornell University Ithaca, New York, United StatesYear of foundationSep 2018CNCAlMgSi alloy90Picture of exhibitGift of Domokos
1868University of California, Berkeley Berkeley, California, United StatesYear of foundationNov 2018CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1877University of Tokyo Tokyo, JapanYear of foundationAug 2018CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Model Collection. Sponsored by Ottó Albrecht
1883University of Auckland Auckland, New ZealandYear of foundationFeb 2017CNCTitanium90Picture of exhibit
1893Sobolev Institute of Mathematics Novosibirsk, RussiaYear of foundation of the city of NovosibirskDec 2019CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1896Hungarian Patent Office Budapest, HungaryYear of foundationNov 2007Rapid prototypingPlastic85Picture of exhibit
1910University of KwaZulu-Natal Durban, South AfricaYear of foundationOct 2015CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht, presented by Hungarian ambassador András Király.
1911University of Regina Regina, Saskatchewan, CanadaYear of foundationMar 2020CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht
1917Chulalongkorn University Bangkok, ThailandYear of foundationMar 2018CNCAlMgSi alloy90Picture of exhibitGift of the Hungarian Embassy
1924Hungarian National Bank Budapest, HungaryYear of foundationAug 2008CNCAlMgSi alloy180Picture of exhibit
1928Institut Henri Poincaré Paris, FranceYear of foundationApr 2011CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Model Collection
1978University of Tromsø - The Arctic University of Norway Tromsø, NorwayYear of foundation of the Department of MathematicsAug 2020CNCAlMgSi alloy90Picture of exhibitPart of the Mathematical Model Collection. Sponsored by Ottó Albrecht.
1996University of Buenos Aires Buenos Aires, ArgentinaYear of naming the Physics Department after Juan José GiambiagiMar 2020CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht, presented by Hungarian ambassador Csaba Gelényi.
2013University of Oxford Oxford, United KingdomYear of opening of the Andrew Wiles Mathematical BuildingFeb 2014CNCStainless steel180Picture of exhibitSponsored by Tim Wong and Ottó Albrecht
2016University of Auckland Auckland, New ZealandYear of opening of the Science CenterFeb 2017CNCClear Plexiglass180Picture of exhibit
2018Instituto Nacional de Matemática Pura e Aplicada Rio de Janeiro, BrazilYear of the International Congress of Mathematicians held in Rio de JaneiroOct 2018CNCAlMgSi alloy90Picture of exhibitSponsored by Ottó Albrecht

Art

The gömböc has inspired a number of artists.

The award-winning short movie Gömböc (2010), directed by Ulrike Vahl, is a character sketch about four misfits who fight with everyday setbacks and barriers and who have one thing in common: if they fall down, then they rise again.[28]

The short film "The Beauty of Thinking" (2012), directed by Márton Szirmai, was a finalist at the GE Focus Forward festival. It tells the story of the discovery of the gömböc.[29][30]

The characteristic shape of the gömböc is curiously reflected in the critically acclaimed novel Climbing Days (2016) by Dan Richards as he describes scenery: "All over Montserrat the landscape reared as gömböc domes and pillars."[31]

A recent solo exhibition of conceptual artist Ryan Gander evolved around the theme of self-righting and featured seven large gömböc shapes gradually covered by black volcanic sand.[32]

The gömböc has also appeared around the globe in art galleries as a recurrent motive in the paintings of Vivien Zhang.[33]

Media

The invention of the gömböc has been in the focus of public and media attention, repeating the success of another Hungarian Ernő Rubik when he designed his cube-shaped puzzle in 1974.[34] For their discovery, Domokos and Várkonyi were decorated with the Knight's Cross of the Republic of Hungary.[35] The New York Times Magazine selected the gömböc as one of the 70 most interesting ideas of the year 2007.[36][37]

The Stamp News website[38] shows the new stamps issued on 30 April 2010, by Hungary, which illustrate a gömböc in different positions. The stamp booklets are arranged in such a manner that the gömböc appears to come to life when the booklet is flipped. The stamps were issued in association with the gömböc on display at the World Expo 2010 (1 May to 31 October). This was also covered by the Linn's Stamp News magazine.[39]

In the internet series Video Game High School, an anthropomorphized gömböc is the antagonist of a children's game being made by the character Ki Swan in the Season 1 episode "Any Game In The House".

The role playing game webcomic Darths and Droids featured (but did not picture) a gömböc as a one-sided die in September 2018.

gollark: Although of course few "immutable" things can stand up to `memmove(id(7), id(8), sys.getsizeof(7))`.
gollark: Uncool.
gollark: How immutable is it? Can you mutate items in it, thus creating apiohazardous conditions?
gollark: I can only be amazed by things with an amazingness quotient above or equal to 0.33338.
gollark: Depends what.

See also

References
  1. Domokos, G.; Varkonyi, P.L. (2008). "Geometry and self-righting of turtles" (free download pdf). Proc. R. Soc. B. 275 (1630): 11–17. doi:10.1098/rspb.2007.1188. PMC 2562404. PMID 17939984.
  2. Summers, Adam (March 2009). "The Living Gömböc. Some tortoise shells evolved the ideal shape for staying upright". Natural History. 118 (2): 22–23.
  3. Ball, Philip (16 October 2007). "How tortoises turn right-side up". Nature News. doi:10.1038/news.2007.170.
  4. Rehmeyer, Julie (5 April 2007). "Can't Knock It Down". Science News.
  5. Hungary Pavilion features Gomboc, expo.shanghaidaily.com (12 July 2010)
  6. New geometric shape "Gomboc" featured at Shanghai Expo, English.news.cn, 19 August 2010
  7. "Világritkaság szobor Budapesten - fotók" (in Hungarian). Retrieved 2 January 2018.
  8. A kis gömböc Archived 20 July 2009 at the Wayback Machine, a folk tale in Hungarian. sk-szeged.hu
  9. Varkonyi, P.L., Domokos, G. (2006). "Mono-monostatic bodies: the answer to Arnold's question" (PDF). The Mathematical Intelligencer. 28 (4): 34–38. doi:10.1007/bf02984701.CS1 maint: multiple names: authors list (link)
  10. Inventors. gomboc-shop.com.
  11. Domokos, Gábor (2008). "My Lunch with Arnol'd" (PDF). The Mathematical Intelligencer. 28 (4): 31. doi:10.1007/BF02984700.
  12. Freiberger, Marianne (May 2009). "The Story of the Gömböc". Plus magazine.
  13. "The first gömböc". gomboc.eu. Archived from the original on 12 November 2017. Retrieved 8 October 2009.
  14. Varkonyi, P.L.; Domokos, G. (2006). "Static Equilibria of Rigid Bodies: Dice, Pebbles, and the Poincare-Hopf Theorem". Journal of Nonlinear Science. 16 (3): 255. doi:10.1007/s00332-005-0691-8.
  15. "Gömböc – Finding Consilience". quickswood.com. 14 February 2008. Archived from the original on 20 February 2015. Retrieved 8 October 2009.
  16. Professor Alexander on the Turtles and the Gömböc. Tetrapod Zoology (24 May 2008).
  17. Domokos, G. Natural numbers, natural shapes. Axiomathes (2018). doi:10.1007/s10516-018-9411-5
  18. Szabó, T., Domokos, G., Grotzinger, J. P. and Jerolmack, D. J. Reconstructing the transport history of pebbles on Mars. Nature Communications Vol. 6, Article number: 8366 (2015).
  19. Domokos, G., Sipos A. Á., Szabó, G. M. and Várkonyi, P. L.: Explaining the Elongated Shape of 'Oumuamua by the Eikonal Abrasion Model. Research Notes of the AAS, Volume 1, No. 1, p. 50 (Dec 2017).
  20. Domokos, G., Jerolmack, D. J., Kun, F. and Török, J. Plato's cube and the natural geometry of fragmentation. Proceedings of the National Academy of Sciences (2020).
  21. Mulgaonkar, Y. et al. Design and fabrication of safe, light-weight flying robots. Proc. ASME Computers and Information in Engineering Conference IDETC/CIE 2015 2–5 August 2015, Massachusetts, US. Paper DETC2015-47864.
  22. Abramson, A. et al. An ingestible self-orienting system for oral delivery of macromolecules. Science, 363(6427) p. 611–615 (2019). doi:10.1126/science.aau2277.
  23. gomboc-online.com.
  24. Usage of a gömböc. gomboc-shop.com.
  25. Does the behavior of a gömböc depend on the size or the material?. gomboc-shop.com.
  26. Knight's Cross for the Gömböc, Gömböc for Arnold Archived 15 September 2009 at the Wayback Machine. Moscow, 20 August 2007. Gomboc.eu.
  27. Individual Gömböc Pieces
  28. Gömböc movie by Ulrike Vahl
  29. The beauty of Thinking by Márton Szirmai on IMDB
  30. The beauty of Thinking by Márton Szirmai on Youtube
  31. Richards, D.: Climbing Days. Faber & Faber, London, 2016.
  32. Gander, R.: The self-righting of all things. Exhibition at Lisson Gallery, London
  33. Vivien Zhang at the Contemporary Art Society
  34. "Boffins develop a 'new shape' called Gomboc". Melbourne: Theage.com.au. 13 February 2007.
  35. A gömböc for the Whipple. News, University of Cambridge (27 April 2009)
  36. Thompson, Clive (9 December 2007) Self-Righting Object, The Archived 15 September 2009 at the Wayback Machine. New York Times Magazine.
  37. Per-Lee, Myra (9 December 2007) Whose Bright Idea Was That? The New York Times Magazine Ideas of 2007. Inventorspot.com.
  38. Better City – Better Life: Shanghai World Expo 2010 Archived 16 August 2017 at the Wayback Machine. Stampnews.com (22 November 2010). Retrieved on 20 October 2016.
  39. McCarty, Denise (28 June 2010) "World of New Issues: Expo stamps picture Hungary's gömböc, Iceland's ice cube". Linn's Stamp News p. 14
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.