Archytas
Archytas (/ˈɑːrkɪtəs/; Greek: Ἀρχύτας; 428–347 BC) was an Ancient Greek philosopher, mathematician, astronomer, statesman, and strategist. He was a scientist of the Pythagorean school and famous for being the reputed founder of mathematical mechanics, as well as a good friend of Plato.
Archytas | |
|---|---|
 Bust from the Villa of the Papyri in Herculaneum, once identified as Archytas, now thought to be Pythagoras[1] | |
| Born | 435 - 410 BC |
| Died | 347 BC (aged 80–81) |
| Era | Pre-Socratic philosophy |
| Region | Western philosophy |
| School | Pythagoreanism |
Notable ideas | Archytas curve |
Influences
| |
Influenced
| |
Life and work
Archytas was born in Tarentum, Magna Graecia and was the son of Mnesagoras or Histiaeus. For a while, he was taught by Philolaus, and was a teacher of mathematics to Eudoxus of Cnidus. Archytas and Eudoxus' student was Menaechmus. As a Pythagorean, Archytas believed that only arithmetic, not geometry, could provide a basis for satisfactory proofs.[2]
Archytas is believed to be the founder of mathematical mechanics.[3] As only described in the writings of Aulus Gellius five centuries after him, he was reputed to have designed and built the first artificial, self-propelled flying device, a bird-shaped model propelled by a jet of what was probably steam, said to have actually flown some 200 meters.[4][5] This machine, which its inventor called The pigeon, may have been suspended on a wire or pivot for its flight.[6][7] Archytas also wrote some lost works, as he was included by Vitruvius in the list of the twelve authors of works of mechanics.[8] Thomas Nelson Winter presents evidence that the pseudo-Aristotelian Mechanical Problems was actually authored by Archytas and misattributed.[9]
Archytas named the harmonic mean, important much later in projective geometry and number theory, though he did not invent it.[10] According to Eutocius, Archytas solved the problem of doubling the cube in his manner (though he believed "that only arithmetic, not geometry", could provide a basis for satisfactory proofs) with a geometric construction.[11] Hippocrates of Chios before, reduced this problem to finding mean proportionals. Archytas' theory of proportions is treated in book VIII of Euclid's Elements, where is the construction for two proportional means, equivalent to the extraction of the cube root. According to Diogenes Laërtius, this demonstration, which uses lines generated by moving figures to construct the two proportionals between magnitudes, was the first in which geometry was studied with concepts of mechanics.[12] The Archytas curve, which he used in his solution of the doubling the cube problem, is named after him.
Politically and militarily, Archytas appears to have been the dominant figure in Tarentum in his generation, somewhat comparable to Pericles in Athens a half-century earlier. The Tarentines elected him strategos, 'general', seven years in a row – a step that required them to violate their own rule against successive appointments. He was allegedly undefeated as a general, in Tarentine campaigns against their southern Italian neighbors. The Seventh Letter of Plato asserts that Archytas attempted to rescue Plato during his difficulties with Dionysius II of Syracuse. In his public career, Archytas had a reputation for virtue as well as efficacy. Some scholars have argued that Archytas may have served as one model for Plato's philosopher king, and that he influenced Plato's political philosophy as expressed in The Republic and other works (i.e., how does a society obtain good rulers like Archytas, instead of bad ones like Dionysius II?).
Archytas may have drowned in a shipwreck in the shore of Mattinata, where his body lay unburied on the shore until a sailor humanely cast a handful of sand on it. Otherwise, he would have had to wander on this side of the Styx for a hundred years, such the virtue of a little dust, munera pulveris, as Horace calls it in Ode 1.28 on which this information on his death is based. The poem, however, is difficult to interpret and it is not certain that the shipwrecked and Archytas are in fact the same person.
The crater Archytas on the Moon is named in his honour.
Archytas curve
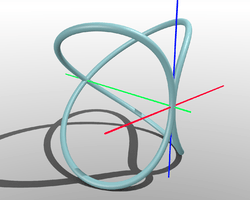
The Archytas curve is created by placing a semicircle (with a diameter of d) on the diameter of one of the two circles of a cylinder (which also has a diameter of d) such that the plane of the semicircle is at right angles to the plane of the circle and then rotating the semicircle about one of its ends in the plane of the cylinder's diameter. This rotation will cut out a portion of the cylinder forming the Archytas curve.[13]
Another way of thinking of this construction is that the Archytas curve is basically the result of cutting out a torus formed by rotating a hemisphere of diameter d out of a cylinder also of diameter d. A cone can go through the same procedures also producing the Archytas curve. Archytas used his curve to determine the construction of a cube with a volume of one third of that of a given cube.
The Delian Problem

One of Archytas' most notable accomplishments comes in the form of a mathematical solution to The Delian Problem, more informally known as doubling the cube. The problem is as follows: given a cube that a side is known, construct a cube with double the original volume. The proof of his model comes from Eudemus, who in the late 4th century wrote a history of geometry, including solutions to this problem from multiple mathematicians and philosophers before him- namely Eudoxus and Menaechmus. Although Eudemus' work did not survive to current day, a transmission of his geometric solution does survive in the form of Eutocius' commentary on Archimedes' De Sphaera et Cylindro. Archytas' solution begins with the concept of mean proportionality and the construction of four similar triangles. Each triangle's hypotenuse and long leg are proportionally similar as the triangle increase in size, which is essentially today's version of similarity of triangles. Archytas then applied the mean proportionals for a given length of a cube. If the volume of the original cube is written as V1 = x3, where x represents the length of a side, we let k1 and k2 represent the proportionality constants, and the cube is then doubled so that a side length is now 2x, a mean proportional between the two can be written as . With the proportionals finished, Archytas completed the solution to his similar triangles as follows: If you cube the proportion of the original length of the side and solve using the mean proportional set, the solution comes to After using light algebra, where the k1 variable represents the edge of the newly doubled cube.
Harmonic Theory
By the time of his analysis, it was known from the Pythagorean diatonic scale that whole numbers alone accounted for musical intervals on a scale. Archytas's work on musical scales included a thorough proof that no mean proportional numbers, like the ones used in his solving of the double cube problem, exist between basic music intervals (the difference in pitch between two sounds). This is to say that the basic interval, does not include any mean proportional number, and cannot then be divided in half. The octave can be doubled without violating this rule, as multiplying a whole number by 2 will always result in a whole number, and can therefore be equated by two mean proportional ratios.
Cosmology
Due to the severe scarcity of resources for Archytas' direct work, it is difficult to pinpoint his exact thoughts on the universe. Through Eudemus and later Simplicius' commentary, however, his thought experiment in regards to the size of the universe remain intact to current day. The experiment is credited as being an influential spark through the early ages, even though Plato nor Aristotle bought the argument. In his experiment for others to participate and decide for themselves, Archytas tells of a scenario in which he is at the effective edge of the fixed stars. He says that if he outreaches his arm, or his stick (staff), that his hand will push the limit of what the edge is. He is then free to move into the newly created space and outstretch his staff once more, thus increasing the limit of space. With his argument, he attested that space, the region of the fixed stars, is infinite.[14] This thought persisted even through modern day, although it is important to note that his model has a defined edge, whereas some current models do not account for a defined edge of space.
Notes
- Archita; Pitagora, Sito ufficiale del Museo Archeologico Nazionale di Napoli, retrieved 25 September 2012
- Morris Kline, Mathematical Thought from Ancient to Modern Times Oxford University Press, 1972 p. 49
- Laërtius 1925, § 83: Vitae philosophorum
- Aulus Gellius, "Attic Nights", Book X, 12.9 at LacusCurtius
- ARCHYTAS OF TARENTUM, Technology Museum of Thessaloniki, Macedonia, Greece Archived December 26, 2008, at the Wayback Machine
- Modern rocketry
- "Automata history". Archived from the original on 2002-12-05. Retrieved 2018-11-28.
- Vitruvius, De architectura, vii.14.
- Thomas Nelson Winter, "The Mechanical Problems in the Corpus of Aristotle," DigitalCommons@University of Nebraska - Lincoln, 2007.
- J. J. O'Connor and E. F. Robertson. Archytas of Tarentum. The MacTutor History of Mathematics archive. Visited 11 August 2011.
- Eutocius, commentary on Archimedes' On the sphere and cylinder.
- Plato blamed Archytas for his contamination of geometry with mechanics (Plutarch, Symposiacs, Book VIII, Question 2): And therefore Plato himself dislikes Eudoxus, Archytas, and Menaechmus for endeavoring to bring down the doubling the cube to mechanical operations; for by this means all that was good in geometry would be lost and corrupted, it falling back again to sensible things, and not rising upward and considering immaterial and immortal images, in which God being versed is always God.
- "Archived copy". Archived from the original on 2008-07-18. Retrieved 2015-03-29.CS1 maint: archived copy as title (link)
- Heath, Thomas Little, Sir (1921). A history of Greek mathematics. New York: Dover Publications. pp. 214. ISBN 0486240738. OCLC 7703465.
References

Further reading
- von Fritz, Kurt (1970). "Archytas of Tarentum". Dictionary of Scientific Biography. 1. New York: Charles Scribner's Sons. pp. 231–233. ISBN 0-684-10114-9. on line
- Huffman, Carl A. Archytas of Tarentum, Cambridge University Press, 2005, ISBN 0-521-83746-4
External links
| Wikiquote has quotations related to: Archytas |
| Wikisource has original works written by or about: Archytas |
| Wikimedia Commons has media related to Archytas. |
- Huffman, Carl. "Archytas". In Zalta, Edward N. (ed.). Stanford Encyclopedia of Philosophy.
- O'Connor, John J.; Robertson, Edmund F., "Archytas", MacTutor History of Mathematics archive, University of St Andrews.
- Pseudo-Aristotle, Mechanica – Greek text and English translation
- Complete fragments (Greek–Spanish bilingual edition)
- Fragments and Life of Archytas
- FARAH CALDERÓN, Walter: Entre la mentira y la verdad pitagórica: el caso de Arquitas de Tarento.