Aristarchus of Samos

Aristarchus of Samos (/ˌærəˈstɑːrkəs/; Greek: Ἀρίσταρχος ὁ Σάμιος, Aristarkhos ho Samios; c. 310 – c. 230 BC) was an ancient Greek astronomer and mathematician who presented the first known heliocentric model that placed the Sun at the center of the known universe with the Earth revolving around it. He was influenced by Philolaus of Croton, but Aristarchus identified the "central fire" with the Sun, and he put the other planets in their correct order of distance around the Sun.[2] Like Anaxagoras before him, he suspected that the stars were just other bodies like the Sun, albeit farther away from Earth. His astronomical ideas were often rejected in favor of the geocentric theories of Aristotle and Ptolemy. Nicolaus Copernicus attributed the heliocentric theory to Aristarchus.[3]

Aristarchus of Samos
Statue of Aristarchus of Samos at the Aristotle University of Thessaloniki
Bornc. 310 BC
Samos
Diedc. 230 BC (age c. 80)
Alexandria[1]
NationalityGreek
Occupation

Heliocentrism
See also: Heliocentrism

The original text has been lost, but a reference in Archimedes' book The Sand Reckoner (Archimedis Syracusani Arenarius & Dimensio Circuli) describes a work in which he advanced the heliocentric model as an alternative hypothesis to geocentrism:

You are now aware ['you' being King Gelon] that the "universe" is the name given by most astronomers to the sphere the centre of which is the centre of the earth, while its radius is equal to the straight line between the centre of the sun and the centre of the earth. This is the common account (τά γραφόμενα) as you have heard from astronomers. But Aristarchus has brought out a book consisting of certain hypotheses, wherein it appears, as a consequence of the assumptions made, that the universe is many times greater than the "universe" just mentioned. His hypotheses are that the fixed stars and the sun remain unmoved, that the earth revolves about the sun on the circumference of a circle, the sun lying in the middle of the orbit, and that the sphere of the fixed stars, situated about the same centre as the sun, is so great that the circle in which he supposes the earth to revolve bears such a proportion to the distance of the fixed stars as the centre of the sphere bears to its surface.[4]

Aristarchus suspected the stars were other suns[5] that are very far away, and that in consequence there was no observable parallax, that is, a movement of the stars relative to each other as the Earth moves around the Sun. Since stellar parallax is only detectable with telescopes, his accurate speculation was unprovable at the time.

It is a common misconception that the heliocentric view was held as sacrilegious by the contemporaries of Aristarchus.[6] Lucio Russo traces this to Gilles Ménage's printing of a passage from Plutarch's On the Apparent Face in the Orb of the Moon, in which Aristarchus jokes with Cleanthes, who is head of the Stoics, a sun worshipper, and opposed to heliocentrism.[6] In the manuscript of Plutarch's text, Aristarchus says Cleanthes should be charged with impiety.[6] Ménage's version, published shortly after the trials of Galileo and Giordano Bruno, transposes an accusative and nominative so that it is Aristarchus who is purported to be impious.[6] The resulting misconception of an isolated and persecuted Aristarchus is still transmitted today.[6][7]

According to Plutarch, while Aristarchus postulated heliocentrism only as a hypothesis, Seleucus of Seleucia, a Hellenistic astronomer who lived a century after Aristarchus, maintained it as a definite opinion and gave a demonstration of it[8] but no full record has been found. In his Naturalis Historia, Pliny the Elder later wondered whether errors in the predictions about the heavens could be attributed to a displacement of the Earth from its central position.[9] Pliny[10] and Seneca[11] referred to the retrograde motion of some planets as an apparent (and not real) phenomenon, which is an implication of heliocentrism rather than geocentrism. Still, no stellar parallax was observed, and Plato, Aristotle, and Ptolemy preferred the geocentric model, which was held as true throughout the Middle Ages.

The heliocentric theory was revived by Copernicus,[12] after which Johannes Kepler described planetary motions with greater accuracy with his three laws. Isaac Newton later gave a theoretical explanation based on laws of gravitational attraction and dynamics.

After realizing that the sun was much larger than the earth and the other planets, Aristarchus concluded that planets revolved around the sun. But this brilliant insight, it turned out, "was too much for the philosophers of the time to swallow and astronomy had to wait 2000 years more to find the right path."[13]

Distance to the Sun (lunar dichotomy)
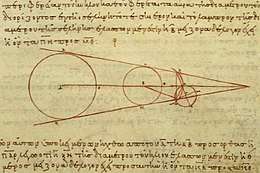
Aristarchus's 3rd-century BC calculations on the relative sizes of (from left) the Sun, Earth and Moon, from a 10th-century AD Greek copy

The only known surviving work usually attributed to Aristarchus, On the Sizes and Distances of the Sun and Moon, is based on a geocentric world view. It has historically been read as stating that the angle subtended by the Sun's diameter is two degrees, but Archimedes states in The Sand Reckoner that Aristarchus had a value of ½ degree, which is much closer to the actual average value of 32' or 0.53 degrees. The discrepancy may come from a misinterpretation of what unit of measure was meant by a certain Greek term in the text of Aristarchus.[14]

Aristarchus claimed that at half moon (first or last quarter moon), the angle between the Sun and Moon was 87°.[15] He might have proposed 87° as a lower bound, since gauging the lunar terminator's deviation from linearity to one degree of accuracy is beyond the unaided human ocular limit (with that limit being about three degrees of accuracy). Aristarchus is known to have also studied light and vision.[16]

Using correct geometry, but the insufficiently accurate 87° datum, Aristarchus concluded that the Sun was between 18 and 20 times farther away than the Moon.[17] (The true value of this angle is close to 89° 50', and the Sun's distance is actually about 400 times that of the Moon.) The implicit false solar parallax of slightly under three degrees was used by astronomers up to and including Tycho Brahe, c. AD 1600. Aristarchus pointed out that the Moon and Sun have nearly equal apparent angular sizes, and therefore their diameters must be in proportion to their distances from Earth; thus, the diameter of the Sun was calculated to be between 18 and 20 times the diameter of the Moon.[18]

gollark: can I use your account too?
gollark: What we really need are holowindows.
gollark: Keanu: the concretegen works now.
gollark: @massimoGG#0000 tablets don't take screens.
gollark: umwn

See also

Notes
  1. "Aristarchus of Samos: Mathematician and astronomer". World History. 8 September 2015. Archived from the original on 7 May 2018. Retrieved 29 November 2018.
  2. Draper, John William (2007) [1874]. "History of the Conflict Between Religion and Science". In Joshi, S. T. (ed.). The Agnostic Reader. Prometheus. pp. 172–173. ISBN 978-1-59102-533-7.
  3. George Kish (1978). A Source Book in Geography. Harvard University Press. p. 51. ISBN 978-0-674-82270-2.
  4. Heath, Thomas (1913), p. 302. The italics and parenthetical comments are as they appear in Heath's original.
  5. Louis Strous. "Who discovered that the Sun was a star?". solar-center.stanford.edu. Retrieved 2014-07-13.
  6. Russo, Lucio (2013-12-01). The Forgotten Revolution: How Science Was Born in 300 BC and Why it Had to Be Reborn. Translated by Levy, Silvio. Springer Science & Business Media. p. 82, fn.106. ISBN 9783642189043. Retrieved 13 June 2017.; Russo, Lucio; Medaglia, Silvio M. (1996). "Sulla presunta accusa di empietà ad Aristarco di Samo". Quaderni Urbinati di Cultura Classica (in Italian). Fabrizio Serra Editore. New Series, Vol. 53 (2): 113–121. doi:10.2307/20547344. JSTOR 20547344.
  7. Plutarch. "De facie quae in orbe lunae apparet, Section 6". Perseus Digital Library. Tufts University. Retrieved 13 June 2017.
  8. Plutarch, Platonicae quaestiones, VIII, i
  9. Neugebauer, O. (1975). A History of Ancient Mathematical Astronomy. Studies in the History of Mathematics and Physical Sciences. 1. Springer-Verlag. pp. 697–698.
  10. Naturalis historia, II, 70
  11. Naturales quaestiones, VII, xxv, 6–7
  12. Joseph A. Angelo (14 May 2014). Encyclopedia of Space and Astronomy. Infobase Publishing. p. 153. ISBN 978-1-4381-1018-9.
  13. Asimov, Isaac (1985). The Greeks: a great adventure. Boston: Houghton Mifflin.
  14. http://www.dioi.org/vols/we0.pdf
  15. Greek Mathematical Works, Loeb Classical Library, Harvard University, 1939–1941, edited by Ivor Thomas, volume 2 (1941), pp. 6–7
  16. Heath, 1913, pp. 299–300; Thomas, 1942, pp. 2–3.
  17. A video on reconstruction of Aristarchus' method, in Turkish without subtitles.
  18. Kragh, Helge (2007). Conceptions of cosmos: from myths to the accelerating universe: a history of cosmology. Oxford University Press. p. 26. ISBN 978-0-19-920916-3.

References

Further reading
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.