Hippocrates of Chios

Hippocrates of Chios (Greek: Ἱπποκράτης ὁ Χῖος; c. 470 – c. 410 BC) was an ancient Greek mathematician, geometer, and astronomer.

This article is about the mathematician. For the Ancient Greek doctor, see Hippocrates.
The Lune of Hippocrates. Partial solution of the "Squaring the circle" task, suggested by Hippocrates. The area of the shaded figure is equal to the area of the triangle ABC. This is not a complete solution of the task (the complete solution is proven to be impossible with compass and straightedge).

He was born on the isle of Chios, where he was originally a merchant. After some misadventures (he was robbed by either pirates or fraudulent customs officials) he went to Athens, possibly for litigation, where he became a leading mathematician.

On Chios, Hippocrates may have been a pupil of the mathematician and astronomer Oenopides of Chios. In his mathematical work there probably was some Pythagorean influence too, perhaps via contacts between Chios and the neighboring island of Samos, a center of Pythagorean thinking: Hippocrates has been described as a 'para-Pythagorean', a philosophical 'fellow traveler'. "Reduction" arguments such as reductio ad absurdum argument (or proof by contradiction) have been traced to him, as has the use of power to denote the square of a line.[1]

Mathematics

The major accomplishment of Hippocrates is that he was the first to write a systematically organized geometry textbook, called Elements (Στοιχεῖα, Stoicheia), that is, basic theorems, or building blocks of mathematical theory. From then on, mathematicians from all over the ancient world could, at least in principle, build on a common framework of basic concepts, methods, and theorems, which stimulated the scientific progress of mathematics.

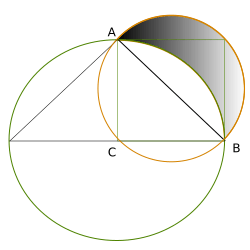
Only a single, famous fragment of Hippocrates' Elements is existent, embedded in the work of Simplicius. In this fragment the area is calculated of some so-called Hippocratic lunes — see Lune of Hippocrates. This was part of a research program to achieve the "quadrature of the circle", that is, to calculate the area of the circle, or, equivalently, to construct a square with the same area as a circle. The strategy, apparently, was to divide a circle into a number of crescent-shaped parts. If it were possible to calculate the area of each of those parts, then the area of the circle as a whole would be known too. Only much later was it proven (by Ferdinand von Lindemann, in 1882) that this approach had no chance of success, because the factor pi (π) is transcendental. The number π is the ratio of the circumference to the diameter of a circle, and also the ratio of the area to the square of the radius.

In the century after Hippocrates, at least four other mathematicians wrote their own Elements, steadily improving terminology and logical structure. In this way, Hippocrates' pioneering work laid the foundation for Euclid's Elements (c. 325 BC), which was to remain the standard geometry textbook for many centuries. Hippocrates is believed to have originated the use of letters to refer to the geometric points and figures in a proposition, e.g., "triangle ABC" for a triangle with vertices at points A, B, and C.

Two other contributions by Hippocrates in the field of mathematics are noteworthy. He found a way to tackle the problem of 'duplication of the cube', that is, the problem of how to construct a cube root. Like the quadrature of the circle, this was another of the so-called three great mathematical problems of antiquity. Hippocrates also invented the technique of 'reduction', that is, to transform specific mathematical problems into a more general problem that is easier to solve. The solution to the more general problem then automatically gives a solution to the original problem.

Astronomy

In the field of astronomy, Hippocrates tried to explain the phenomena of comets and the Milky Way. His ideas have not been handed down very clearly, but he probably thought both were optical illusions, the result of refraction of solar light by moisture that was exhaled by, respectively, a putative planet near the Sun, and the stars. The fact that Hippocrates thought that light rays originated in our eyes instead of in the object that is seen, adds to the unfamiliar character of his ideas.

Notes
  1. W. W. Rouse Ball, A Short Account of the History of Mathematics (1888) p. 36.
gollark: There are quite a lot of laws *in general*, enough that you can't practically know what they all are.
gollark: It's an "autonomous commune" in... Seattle or something.
gollark: It's apparently big enough that you would need something like 20 high-end compute GPUs, so... quite a lot of raspberry pis.
gollark: The trouble with this is that scaling it up like this requires ridiculous amounts of computing resources, and now it's so big that individuals probably can't even tractably run it.
gollark: It can add somewhat larger numbers!

References
  • Ivor Bulmer-Thomas, 'Hippocrates of Chios', in: Dictionary of Scientific Biography, Charles Coulston Gillispie, ed. (18 Volumes, New York 1970–1990) pp. 410–418.
  • [Axel Anthon] Björnbo, 'Hippokrates', in: Paulys Realencyclopädie der Classischen Altertumswissenschaft, G. Wissowa, ed. (51 Volumes; 1894–1980) Vol. 8 (1913) col. 1780–1801.
  • O'Connor, John J.; Robertson, Edmund F., "Hippocrates of Chios", MacTutor History of Mathematics archive, University of St Andrews.
  • The Quadrature of the Circle and Hippocrates' Lunes at Convergence
  • Mesolabe Compass and Square Roots - Numberphile video explaining Hippocrates' mesolabe compass
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.