600-cell
In geometry, the 600-cell is the convex regular 4-polytope (four-dimensional analogue of a Platonic solid) with Schläfli symbol {3,3,5}. It is also called a C600, hexacosichoron[1] and hexacosihedroid.[2]
| 600-cell | |
|---|---|
 Schlegel diagram, vertex-centered (vertices and edges) | |
| Type | Convex regular 4-polytope |
| Schläfli symbol | {3,3,5} |
| Coxeter diagram | |
| Cells | 600 (3.3.3) |
| Faces | 1200 {3} |
| Edges | 720 |
| Vertices | 120 |
| Vertex figure |  icosahedron |
| Petrie polygon | 30-gon |
| Coxeter group | H4, [3,3,5], order 14400 |
| Dual | 120-cell |
| Properties | convex, isogonal, isotoxal, isohedral |
| Uniform index | 35 |
The 600-cell is regarded as the 4-dimensional analog of the icosahedron, since it has five tetrahedra meeting at every edge, just as the icosahedron has five triangles meeting at every vertex. It is also called a tetraplex (abbreviated from "tetrahedral complex") and polytetrahedron, being bounded by tetrahedral cells.
Geometry
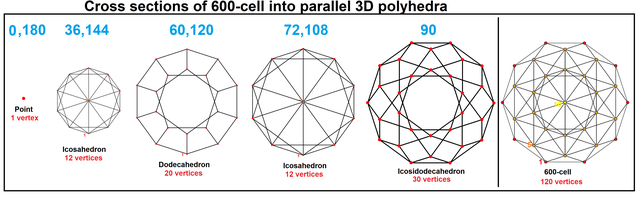
Its boundary is composed of 600 tetrahedral cells with 20 meeting at each vertex. Together they form 1200 triangular faces, 720 edges, and 120 vertices. The edges form 72 flat regular decagons. Each vertex of the 600-cell is a vertex of six such decagons.
The mutual distances of the vertices, measured in degrees of arc on the circumscribed hypersphere, only have the values 36° = π/5, 60° = π/3, 72° = 2π/5, 90° = π/2, 108° = 3π/5, 120° = 2π/3, 144° = 4π/5, and 180° = π. Departing from an arbitrary vertex V one has at 36° and 144° the 12 vertices of an icosahedron, at 60° and 120° the 20 vertices of a dodecahedron, at 72° and 108° again the 12 vertices of an icosahedron, at 90° the 30 vertices of an icosidodecahedron, and finally at 180° the antipodal vertex of V.[3] These can be seen in the H3 Coxeter plane projections with overlapping vertices colored. Just like the icosidodecahedron can be partitioned into 6 central decagons (60 edge = 6×10), the 600-cell can be partitioned into 72 decagons (720 edges = 72 × 10).
Its vertex figure is an icosahedron, and its dual polytope is the 120-cell, with which it can form a compound. It has a dihedral angle of π/3 + arccos(−1/4) ≈ 164.4775°.[4]
Each cell touches, in some manner, 56 other cells. One cell contacts each of the four faces; two cells contact each of the six edges, but not a face; and ten cells contact each of the four vertices, but not a face or edge.
As a configuration
This configuration matrix represents the 600-cell. The rows and columns correspond to vertices, edges, faces, and cells. The diagonal numbers say how many of each element occur in the whole 600-cell. The nondiagonal numbers say how many of the column's element occur in or at the row's element.[5][6]
Here is the configuration expanded with k-face elements and k-figures. The diagonal element counts are the ratio of the full Coxeter group order, 14400, divided by the order of the subgroup with mirror removal.
| H4 | k-face | fk | f0 | f1 | f2 | f3 | k-fig | Notes | |
|---|---|---|---|---|---|---|---|---|---|
| H3 | ( ) | f0 | 120 | 12 | 30 | 20 | {3,5} | H4/H3 = 14400/120 = 120 | |
| A1H2 | { } | f1 | 2 | 720 | 5 | 5 | {5} | H4/H2A1 = 14400/10/2 = 720 | |
| A2A1 | {3} | f2 | 3 | 3 | 1200 | 2 | { } | H4/A2A1 = 14400/6/2 = 1200 | |
| A3 | {3,3} | f3 | 4 | 6 | 4 | 600 | ( ) | H4/A3 = 14400/24 = 600 |
Coordinates
The vertices of a 600-cell centered at the origin of 4-space, with edges of length 1/φ (where φ = 1 + √5/2 is the golden ratio), can be given as follows: 16 vertices of the form:[7]
- (±1/2, ±1/2, ±1/2, ±1/2),
and 8 vertices obtained from
- (0, 0, 0, ±1)
by permuting coordinates. The remaining 96 vertices are obtained by taking even permutations of
- 1/2(±φ, ±1, ±1/φ, 0).
Note that the first 16 vertices are the vertices of a tesseract, the second eight are the vertices of a 16-cell, and that all 24 vertices together are vertices of a 24-cell. The final 96 vertices are the vertices of a snub 24-cell, which can be found by partitioning each of the 96 edges of another 24-cell (dual to the first) in the golden ratio in a consistent manner.
When interpreted as quaternions, the 120 vertices of the 600-cell form a group under quaternionic multiplication. This group is often called the binary icosahedral group and denoted by 2I as it is the double cover of the ordinary icosahedral group I. It occurs twice in the rotational symmetry group RSG of the 600-cell as an invariant subgroup, namely as the subgroup 2IL of quaternion left-multiplications and as the subgroup 2IR of quaternion right-multiplications. Each rotational symmetry of the 600-cell is generated by specific elements of 2IL and 2IR; the pair of opposite elements generate the same element of RSG. The centre of RSG consists of the non-rotation Id and the central inversion −Id. We have the isomorphism RSG ≅ (2IL × 2IR) / {Id, -Id}. The order of RSG equals 120 × 120/2 = 7200.
The binary icosahedral group is isomorphic to SL(2,5).
The full symmetry group of the 600-cell is the Weyl group of H4. This is a group of order 14400. It consists of 7200 rotations and 7200 rotation-reflections. The rotations form an invariant subgroup of the full symmetry group. The rotational symmetry group was described by S.L. van Oss (1899); see References.
Visualization
The symmetries of the 3-D surface of the 600-cell are somewhat difficult to visualize due to both the large number of tetrahedral cells, and the fact that the tetrahedron has no opposing faces or vertices. One can start by realizing the 600-cell is the dual of the 120-cell. One may also notice that the 600-cell also contains the vertices of a dodecahedron, which with some effort can be seen in most of the below perspective projections.
A three-dimensional model of the 600-cell, in the collection of the Institut Henri Poincaré, was photographed in 1934–1935 by Man Ray, and formed part of two of his later "Shakesperean Equation" paintings.[8]
Union of two tori
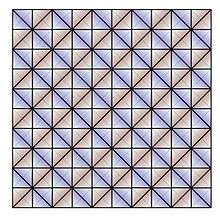
The 120-cell can be decomposed into two disjoint tori. Since it is the dual of the 600-cell, this same dual tori structure exists in the 600-cell, although it is somewhat more complex. The 10-cell geodesic path in the 120-cell corresponds to a 10-vertex decagon path in the 600-cell. Start by assembling five tetrahedra around a common edge. This structure looks somewhat like an angular "flying saucer". Stack ten of these, vertex to vertex, "pancake" style. Fill in the annular ring between each "saucer" with 10 tetrahedra forming an icosahedron. You can view this as five, vertex stacked, icosahedral pyramids, with the five extra annular ring gaps also filled in. The surface is the same as that of ten stacked pentagonal antiprisms. You now have a torus consisting of 150 cells, ten edges long, with 100 exposed triangular faces, 150 exposed edges, and 50 exposed vertices. Stack another tetrahedron on each exposed face. This will give you a somewhat bumpy torus of 250 cells with 50 raised vertices, 50 valley vertices, and 100 valley edges. The valleys are 10 edge long closed paths and correspond to other instances of the 10-vertex decagon path mentioned above. These paths spiral around the center core path, but mathematically they are all equivalent. Build a second identical torus of 250 cells that interlinks with the first. This accounts for 500 cells. These two tori mate together with the valley vertices touching the raised vertices, leaving 100 tetrahedral voids that are filled with the remaining 100 tetrahedra that mate at the valley edges. This latter set of 100 tetrahedra are on the exact boundary of the duocylinder and form a clifford torus. They can be "unrolled" into a square 10x10 array. Incidentally this structure forms one tetrahedral layer in the tetrahedral-octahedral honeycomb.
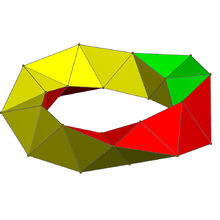 A single 30-tetrahedron ring Boerdijk–Coxeter helix within the 600-cell, seen stereographic projection |
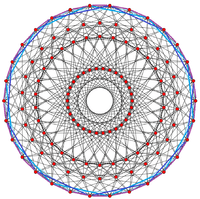 A 30-tetrahedron ring can be seen along the perimeter of this 30-gonal orthogonal projection |
There are exactly 50 "egg crate" recesses and peaks on both sides that mate with the 250 cell tori. In this case into each recess, instead of an octahedron as in the honeycomb, fits a triangular bipyramid composed of two tetrahedra.
The 600-cell can be further partitioned into 20 disjoint intertwining rings of 30 cells and ten edges long each, forming a discrete Hopf fibration. These chains of 30 tetrahedra each form a Boerdijk–Coxeter helix. Five such helices nest and spiral around each of the 10-vertex decagon paths, forming the initial 150 cell torus mentioned above.
This decomposition of the 600-cell has symmetry [[10,2+,10]], order 400, the same symmetry as the grand antiprism. The grand antiprism is just the 600-cell with the two above 150-cell tori removed, leaving only the single middle layer of tetrahedra, similar to the belt of an icosahedron with the 5 top and 5 bottom triangles removed (pentagonal antiprism).
Images
2D projections
The H3 decagonal projection shows the plane of the van Oss polygon.
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
3D projections
| Vertex-first projection | |
|---|---|
 |
This image shows a vertex-first perspective projection of the 600-cell into 3D. The 600-cell is scaled to a vertex-center radius of 1, and the 4D viewpoint is placed 5 units away. Then the following enhancements are applied:
|
| Cell-first projection. | |
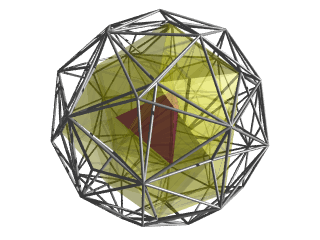 |
This image shows the 600-cell in cell-first perspective projection into 3D. Again, the 600-cell to a vertex-center radius of 1 and the 4D viewpoint is placed 5 units away. The following enhancements are then applied:
This particular viewpoint shows a nice outline of 5 tetrahedra sharing an edge, towards the front of the 3D image. |
| Simple Rotation | |
 |
A 3D projection of a 600-cell performing a simple rotation. |
| Concentric Hulls | |
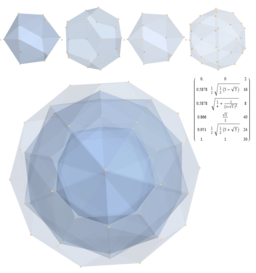 |
The 600-cell is projected to 3D using an orthonormal basis. The vertices are sorted and tallied by their 3D norm. Generating the increasingly transparent hull of each set of tallied norms shows pairs of: 1) points at the origin |
Stereographic
| Stereographic projection (on 3-sphere) | |
|---|---|
 |
Cell-Centered. The 720 edges of the 600-cell can be seen here as 72 circles, each divided into 10 arc-edges at the intersections. Each vertex has 6 circles intersecting. |
Diminished 600-cells
The snub 24-cell may be obtained from the 600-cell by removing the vertices of an inscribed 24-cell and taking the convex hull of the remaining vertices. This process is a diminishing of the 600-cell.
The grand antiprism may be obtained by another diminishing of the 600-cell: removing 20 vertices that lie on two mutually orthogonal rings and taking the convex hull of the remaining vertices.
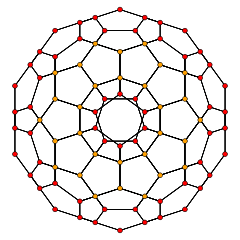
A bi-24-diminished 600-cell, with all tridiminished icosahedron cells has 48 vertices removed, leaving 72 of 120 vertices of the 600-cell. The dual of a bi-24-diminished 600-cell, is a tri-24-diminished 600-cell, with 48 vertices and 72 hexahedron cells.
There are a total of 314,248,344 diminishings of the cell by non-adjacent vertices. All of these consist of regular tetrahedral and icosahedral cells.[9]
| Diminished 600-cells | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Name | Tri-24-diminished 600-cell | Bi-24-diminished 600-cell | Snub 24-cell (24-diminished 600-cell) |
Grand antiprism (20-diminished 600-cell) |
600-cell | ||||||
| Vertices | 48 | 72 | 96 | 100 | 120 | ||||||
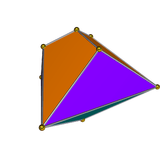
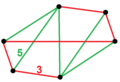
| Vertex figure (Symmetry) |
 dual of tridiminished icosahedron ([3], order 6) |
 tetragonal antiwedge ([2]+, order 2) |
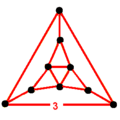 tridiminished icosahedron ([3], order 6) |
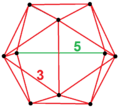 bidiminished icosahedron ([2], order 4) |
 Icosahedron ([5,3], order 120) | ||||||
| Symmetry | Order 144 (48×3 or 72×2) | [3+,4,3] Order 576 (96×6) |
[[10,2+,10]] Order 400 (100×4) |
[5,3,3] Order 14400 (120×120) | |||||||
| Net |  |
 |
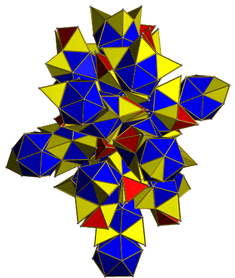 |
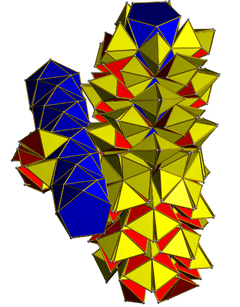 |
 | ||||||
| Ortho H4 plane |
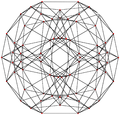 |
 |
 |
 | |||||||
| Ortho F4 plane |
 |
 |
 |
 | |||||||
Related complex polygons
The regular complex polytopes 3{5}3, ![]()
![]()
![]()
![]()
![]()
![]()
| Regular complex polytope in orthogonal projection of H4 Coxeter plane | ||
|---|---|---|
 {3,3,5} Order 14400 |
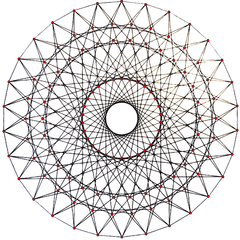 3{5}3 Order 360 |
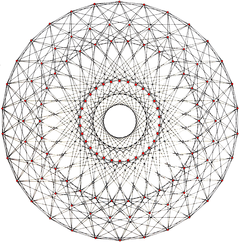 5{3}5 Order 600 |
Related polytopes and honeycombs
The 600-cell is one of 15 regular and uniform polytopes with the same symmetry [3,3,5]:
| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
 |
 |
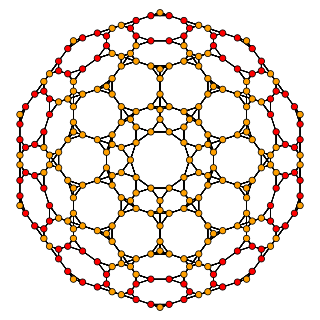 |
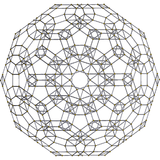 |
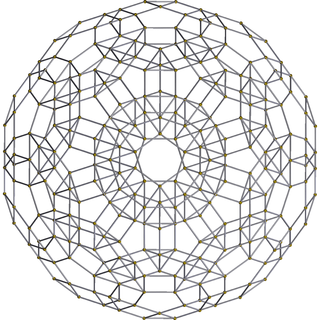 |
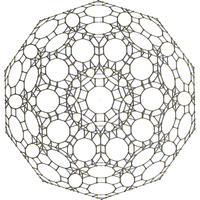 |
 |
 | ||||
 |
 |
 |
 |
 |
 |
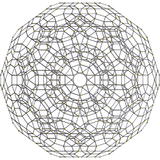 | |||||
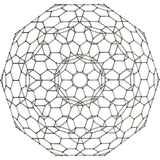
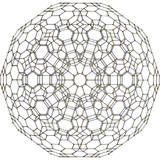
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
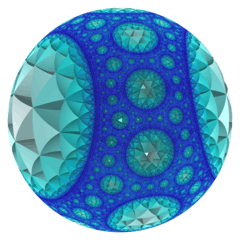
It is similar to three regular 4-polytopes: the 5-cell {3,3,3}, 16-cell {3,3,4} of Euclidean 4-space, and the order-6 tetrahedral honeycomb {3,3,6} of hyperbolic space. All of these have a tetrahedral cells.
| {3,3,p} polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||||||
| Form | Finite | Paracompact | Noncompact | ||||||||
| Name | {3,3,3} |
{3,3,4} |
{3,3,5} |
{3,3,6} |
{3,3,7} |
{3,3,8} |
... {3,3,∞} | ||||
| Image |  |
 |
 |
 |
 |
 |
 | ||||
| Vertex figure |
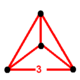 {3,3} |
 {3,4} |
 {3,5} |
 {3,6} |
 {3,7} |
 {3,8} |
 {3,∞} | ||||
This 4-polytope is a part of a sequence of 4-polytope and honeycombs with icosahedron vertex figures:
| {p,3,5} polytopes | |||||||
|---|---|---|---|---|---|---|---|
| Space | S3 | H3 | |||||
| Form | Finite | Compact | Paracompact | Noncompact | |||
| Name | {3,3,5} |
{4,3,5} |
{5,3,5} |
{6,3,5} |
{7,3,5} |
{8,3,5} |
... {∞,3,5} |
| Image |  |
 |
 |
 |
 |
 |
 |
| Cells | {3,3} |
{4,3} |
{5,3} |
{6,3} |
{7,3} |
{8,3} |
{∞,3} |
See also
- Uniform 4-polytope family with [5,3,3] symmetry
- Regular 4-polytope
- 120-cell, the dual 4-polytope to the 600-cell
Notes
- N.W. Johnson: Geometries and Transformations, (2018) ISBN 978-1-107-10340-5 Chapter 11: Finite Symmetry Groups, 11.5 Spherical Coxeter groups, p.249
- Matila Ghyka, The Geometry of Art and Life (1977), p.68
- S.L. van Oss (1899); F. Buekenhout and M. Parker (1998)
- Coxeter, Regular polygons, 3rd edition, Dover Publications, p.293, ≈164°29′
- Coxeter, Regular Polytopes, sec 1.8 Configurations
- Coxeter, Complex Regular Polytopes, p.117
- Weisstein, Eric W. "600-cell". MathWorld.
- Grossman, Wendy A.; Sebline, Edouard, eds. (2015), Man Ray Human Equations: A journey from mathematics to Shakespeare, Hatje Cantz. See in particular mathematical object mo-6.2, p. 58; Antony and Cleopatra, SE-6, p. 59; mathematical object mo-9, p. 64; Merchant of Venice, SE-9, p. 65, and "The Hexacosichoron", Philip Ordning, p. 96.
- Sikiric, Mathieu; Myrvold, Wendy (2007). "The special cuts of 600-cell". Beiträge zur Algebra und Geometrie. 49 (1).
- Coxeter, H. S. M., Regular Complex Polytopes, second edition, Cambridge University Press, (1991). pp.48-49
References
- H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
- Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation
- Oss, Salomon Levi van: Das regelmässige 600-Zell und seine selbstdeckenden Bewegungen. Verhandelingen der Koninklijke (Nederlandse) Akademie van Wetenschappen, Sectie 1 Deel 7 Nummer 1 (Afdeeling Natuurkunde). Amsterdam: 1899. Online at URL , reachable from the home page of the KNAW Digital Library at URL . REMARK: Van Oss does not mention the arc distances between vertices of the 600-cell.
- F. Buekenhout, M. Parker: The number of nets of the regular convex polytopes in dimension <= 4. Discrete Mathematics, Volume 186, Issues 1-3, 15 May 1998, Pages 69-94. REMARK: The authors do mention the arc distances between vertices of the 600-cell.
External links
- Weisstein, Eric W. "600-Cell". MathWorld.
- Olshevsky, George. "Hexacosichoron". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Klitzing, Richard. "4D uniform polytopes (polychora) x3o3o5o - ex".
- Der 600-Zeller (600-cell) Marco Möller's Regular polytopes in R4 (German)
- The 600-Cell Vertex centered expansion of the 600-cell
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||