6-simplex
In geometry, a 6-simplex is a self-dual regular 6-polytope. It has 7 vertices, 21 edges, 35 triangle faces, 35 tetrahedral cells, 21 5-cell 4-faces, and 7 5-simplex 5-faces. Its dihedral angle is cos−1(1/6), or approximately 80.41°.
| 6-simplex | |
|---|---|
| Type | uniform polypeton |
| Schläfli symbol | {35} |
| Coxeter diagrams | |
| Elements |
f5 = 7, f4 = 21, C = 35, F = 35, E = 21, V = 7 |
| Coxeter group | A6, [35], order 5040 |
| Bowers name and (acronym) | Heptapeton (hop) |
| Vertex figure | 5-simplex |
| Circumradius | 0.645497 |
| Properties | convex, isogonal self-dual |
Alternate names
It can also be called a heptapeton, or hepta-6-tope, as a 7-facetted polytope in 6-dimensions. The name heptapeton is derived from hepta for seven facets in Greek and -peta for having five-dimensional facets, and -on. Jonathan Bowers gives a heptapeton the acronym hop.[1]
As a configuration
This configuration matrix represents the 6-simplex. The rows and columns correspond to vertices, edges, faces, cells, 4-faces and 5-faces. The diagonal numbers say how many of each element occur in the whole 6-simplex. The nondiagonal numbers say how many of the column's element occur in or at the row's element. This self-dual simplex's matrix is identical to its 180 degree rotation.[2][3]
Coordinates
The Cartesian coordinates for an origin-centered regular heptapeton having edge length 2 are:
The vertices of the 6-simplex can be more simply positioned in 7-space as permutations of:
- (0,0,0,0,0,0,1)
This construction is based on facets of the 7-orthoplex.
Images
| Ak Coxeter plane | A6 | A5 | A4 |
|---|---|---|---|
| Graph |  |
 |
 |
| Dihedral symmetry | [7] | [6] | [5] |
| Ak Coxeter plane | A3 | A2 | |
| Graph |  |
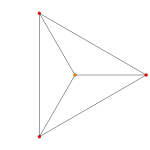 | |
| Dihedral symmetry | [4] | [3] |
Related uniform 6-polytopes
The regular 6-simplex is one of 35 uniform 6-polytopes based on the [3,3,3,3,3] Coxeter group, all shown here in A6 Coxeter plane orthographic projections.
| A6 polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
 t0 |
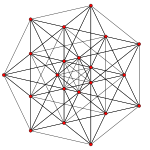 t1 |
 t2 |
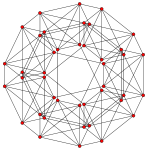 t0,1 |
 t0,2 |
 t1,2 |
 t0,3 |
 t1,3 |
 t2,3 | |||
 t0,4 |
 t1,4 |
 t0,5 |
 t0,1,2 |
 t0,1,3 |
 t0,2,3 |
 t1,2,3 |
 t0,1,4 |
 t0,2,4 | |||
 t1,2,4 |
 t0,3,4 |
 t0,1,5 |
 t0,2,5 |
 t0,1,2,3 |
 t0,1,2,4 |
 t0,1,3,4 |
 t0,2,3,4 |
 t1,2,3,4 | |||
 t0,1,2,5 |
 t0,1,3,5 |
 t0,2,3,5 |
 t0,1,4,5 |
 t0,1,2,3,4 |
 t0,1,2,3,5 |
 t0,1,2,4,5 |
 t0,1,2,3,4,5 | ||||
Notes
- Klitzing, Richard. "6D uniform polytopes (polypeta) x3o3o3o3o3o — hop".
- Coxeter 1973, §1.8 Configurations
- Coxeter, H.S.M. (1991). Regular Complex Polytopes (2nd ed.). Cambridge University Press. p. 117. ISBN 9780521394901.
References
- Coxeter, H.S.M.:
- — (1973). "Table I (iii): Regular Polytopes, three regular polytopes in n-dimensions (n≥5)". Regular Polytopes (3rd ed.). Dover. p. 296. ISBN 0-486-61480-8.
- Sherk, F. Arthur; McMullen, Peter; Thompson, Anthony C.; Weiss, Asia Ivic, eds. (1995). Kaleidoscopes: Selected Writings of H.S.M. Coxeter. Wiley. ISBN 978-0-471-01003-6.
- (Paper 22) — (1940). "Regular and Semi Regular Polytopes I". Math. Zeit. 46: 380–407. doi:10.1007/BF01181449.
- (Paper 23) — (1985). "Regular and Semi-Regular Polytopes II". Math. Zeit. 188: 559–591. doi:10.1007/BF01161657.
- (Paper 24) — (1988). "Regular and Semi-Regular Polytopes III". Math. Zeit. 200: 3–45. doi:10.1007/BF01161745.
- Conway, John H.; Burgiel, Heidi; Goodman-Strass, Chaim (2008). "26. Hemicubes: 1n1". The Symmetries of Things. p. 409. ISBN 978-1-56881-220-5.
- Johnson, Norman (1991). "Uniform Polytopes" (Manuscript). Cite journal requires
|journal=(help)- Johnson, N.W. (1966). The Theory of Uniform Polytopes and Honeycombs (PhD). University of Toronto. OCLC 258527038.
External links
- Olshevsky, George. "Simplex". Glossary for Hyperspace. Archived from the original on 4 February 2007.
- Polytopes of Various Dimensions
- Multi-dimensional Glossary
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||