Icosahedral 120-cell

In geometry, the icosahedral 120-cell, polyicosahedron, faceted 600-cell or icosaplex is a regular star 4-polytope with Schläfli symbol {3,5,5/2}. It is one of 10 regular Schläfli-Hess polytopes.

Icosahedral 120-cell

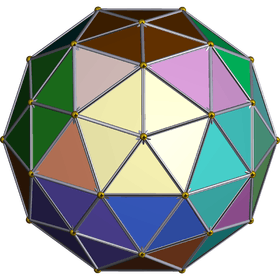Orthogonal projection
TypeSchläfli-Hess polytope
Cells120 {3,5}
Faces1200 {3}
Edges720
Vertices120
Vertex figure{5,5/2}
Schläfli symbol{3,5,5/2}
Symmetry groupH4, [3,3,5]
Coxeter-Dynkin diagram
DualSmall stellated 120-cell
PropertiesRegular

It is constructed by 5 icosahedra around each edge in a pentagrammic figure. The vertex figure is a great dodecahedron.

It has the same edge arrangement as the 600-cell, grand 120-cell and great 120-cell, and shares its vertices with all other Schläfli–Hess 4-polytopes except the great grand stellated 120-cell (another stellation of the 120-cell).

Orthographic projections by Coxeter planes
H4 - F4

[30]
[20]
[12]
H3 A2 / B3 / D4 A3 / B2

[10]
[6]
[4]

As a faceted 600-cell, replacing the simplicial cells of the 600-cell with icosahedral pentagonal polytope cells, it could be seen as a four-dimensional analogue of the great dodecahedron, which replaces the triangular faces of the icosahedron with pentagonal faces. Indeed, the icosahedral 120-cell is dual to the small stellated 120-cell, which could be taken as a 4D analogue of the small stellated dodecahedron, dual of the great dodecahedron. With its dual, it can form the compound of icosahedral 120-cell and small stellated 120-cell.

gollark: Technically, it doesn't.
gollark: But you could just have Discord open instead.
gollark: "hmm yes I will just check my email to see who has pinged me on discord" - silly people
gollark: What WERE they THINKING this WOULD be USEFUL for?
gollark: Why did discord EMAIL me with my mentions?

See also
  • List of regular polytopes
  • Convex regular 4-polytope
  • Kepler-Poinsot solids - regular star polyhedron
  • Star polygon - regular star polygons

References
  • Edmund Hess, (1883) Einleitung in die Lehre von der Kugelteilung mit besonderer Berücksichtigung ihrer Anwendung auf die Theorie der Gleichflächigen und der gleicheckigen Polyeder .
  • H. S. M. Coxeter, Regular Polytopes, 3rd. ed., Dover Publications, 1973. ISBN 0-486-61480-8.
  • John H. Conway, Heidi Burgiel, Chaim Goodman-Strass, The Symmetries of Things 2008, ISBN 978-1-56881-220-5 (Chapter 26, Regular Star-polytopes, pp. 404–408)
  • Klitzing, Richard. "4D uniform polytopes (polychora) x3o5o5/2o - fix".
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.