Rectified 600-cell
In geometry, the rectified 600-cell or rectified hexacosichoron is a convex uniform 4-polytope composed of 600 regular octahedra and 120 icosahedra cells. Each edge has two octahedra and one icosahedron. Each vertex has five octahedra and two icosahedra. In total it has 3600 triangle faces, 3600 edges, and 720 vertices.
| Rectified 600-cell | |
|---|---|
 Schlegel diagram, shown as Birectified 120-cell, with 119 icosahedral cells colored | |
| Type | Uniform 4-polytope |
| Uniform index | 34 |
| Schläfli symbol | t1{3,3,5} or r{3,3,5} |
| Coxeter-Dynkin diagram | |
| Cells | 600 (3.3.3.3) 120 {3,5} |
| Faces | 1200+2400 {3} |
| Edges | 3600 |
| Vertices | 720 |
| Vertex figure | 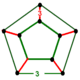 pentagonal prism |
| Symmetry group | H4, [3,3,5], order 14400 |
| Properties | convex, vertex-transitive, edge-transitive |
Containing the cell realms of both the regular 120-cell and the regular 600-cell, it can be considered analogous to the polyhedron icosidodecahedron, which is a rectified icosahedron and rectified dodecahedron.
The vertex figure of the rectified 600-cell is a uniform pentagonal prism.
Semiregular polytope
It is one of three semiregular 4-polytopes made of two or more cells which are Platonic solids, discovered by Thorold Gosset in his 1900 paper. He called it a octicosahedric for being made of octahedron and icosahedron cells.
E. L. Elte identified it in 1912 as a semiregular polytope, labeling it as tC600.
Alternate names
- octicosahedric (Thorold Gosset)
- Icosahedral hexacosihecatonicosachoron
- Rectified 600-cell (Norman W. Johnson)
- Rectified hexacosichoron
- Rectified polytetrahedron
- Rox (Jonathan Bowers)
Images
| H4 | - | F4 |
|---|---|---|
 [30] |
 [20] |
 [12] |
| H3 | A2 / B3 / D4 | A3 / B2 |
 [10] |
 [6] |
 [4] |
| Stereographic projection | Net |
|---|---|
 |
 |
Related polytopes
Diminished rectified 600-cell
| 120-diminished rectified 600-cell | |
|---|---|
| Type | 4-polytope |
| Cells | 840 cells: 600 square pyramid 120 pentagonal prism 120 pentagonal antiprism |
| Faces | 2640: 1800 {3} 600 {4} 240 {5} |
| Edges | 2400 |
| Vertices | 600 |
| Vertex figure | 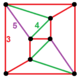 Bi-diminished pentagonal prism (1) 3.3.3.3 + (4) 3.3.4 (2) 4.4.5 (2) 3.3.3.5 |
| Symmetry group | 1/12[3,3,5], order 1200 |
| Properties | convex |
A related vertex-transitive polytope can be constructed with equal edge lengths removes 120 vertices from the rectified 600-cell, but isn't uniform because it contains square pyramid cells,[1] discovered by George Olshevsky, calling it a swirlprismatodiminished rectified hexacosichoron, with 840 cells (600 square pyramids, 120 pentagonal prisms, and 120 pentagonal antiprisms), 2640 faces (1800 triangles, 600 square, and 240 pentagons), 2400 edges, and 600 vertices. It has a chiral bi-diminished pentagonal prism vertex figure.
Each removed vertex creates a pentagonal prism cell, and diminishes two neighboring icosahedra into pentagonal antiprisms, and each octahedron into a square pyramid.[2]
This polytope can be partitioned into 12 rings of alternating 10 pentagonal prisms and 10 antiprisms, and 30 rings of square pyramids.
| Schlegel diagram | Orthogonal projection |
|---|---|
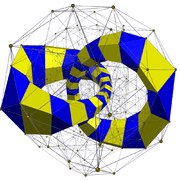 Two orthogonal rings shown |
 2 rings of 30 red square pyramids, one ring along perimeter, and one centered. |

Net
H4 family
| H4 family polytopes | |||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| 120-cell | rectified 120-cell |
truncated 120-cell |
cantellated 120-cell |
runcinated 120-cell |
cantitruncated 120-cell |
runcitruncated 120-cell |
omnitruncated 120-cell | ||||
| {5,3,3} | r{5,3,3} | t{5,3,3} | rr{5,3,3} | t0,3{5,3,3} | tr{5,3,3} | t0,1,3{5,3,3} | t0,1,2,3{5,3,3} | ||||
 |
 |
 |
 |
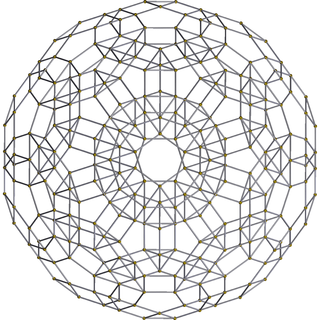 |
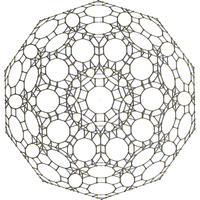 |
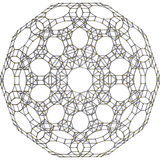 |
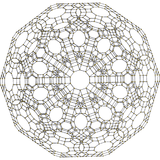 | ||||
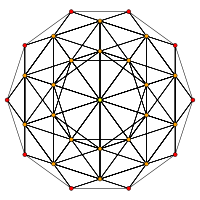 |
 |
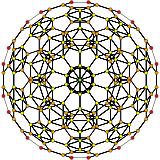 |
 |
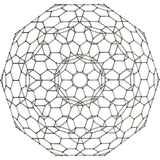 |
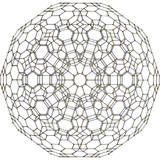 |
 | |||||
| 600-cell | rectified 600-cell |
truncated 600-cell |
cantellated 600-cell |
bitruncated 600-cell |
cantitruncated 600-cell |
runcitruncated 600-cell |
omnitruncated 600-cell | ||||
| {3,3,5} | r{3,3,5} | t{3,3,5} | rr{3,3,5} | 2t{3,3,5} | tr{3,3,5} | t0,1,3{3,3,5} | t0,1,2,3{3,3,5} | ||||
Pentagonal prism vertex figures
| Space | S3 | H3 | ||||
|---|---|---|---|---|---|---|
| Form | Finite | Compact | Paracompact | Noncompact | ||
| Name | r{3,3,5} |
r{4,3,5} |
r{5,3,5} |
r{6,3,5} |
r{7,3,5} |
... r{∞,3,5} |
| Image |  |
 |
 |
 |
||
| Cells {3,5} |
r{3,3} |
r{4,3} |
r{5,3} |
r{6,3} |
r{7,3} |
r{∞,3} |
References
- Category S4: Scaliform Swirlprisms spidrox
- Klitzing, Richard. "4D convex scaliform polychora swirlprismatodiminished rectified hexacosachoron".
- Kaleidoscopes: Selected Writings of H. S. M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
- (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
- (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
- (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
- J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
- N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
- Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation
External links
- Convex uniform polychora based on the hecatonicosachoron (120-cell) and hexacosichoron (600-cell) - Model 34, George Olshevsky.
- Klitzing, Richard. "4D uniform polytopes (polychora) o3x3o5o - rox".
- Archimedisches Polychor Nr. 45 (rectified 600-cell) Marco Möller's Archimedean polytopes in R4 (German)
- H4 uniform polytopes with coordinates: r{3,3,5}
Fundamental convex regular and uniform polytopes in dimensions 2–10 | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Family | An | Bn | I2(p) / Dn | E6 / E7 / E8 / F4 / G2 | Hn | |||||||
| Regular polygon | Triangle | Square | p-gon | Hexagon | Pentagon | |||||||
| Uniform polyhedron | Tetrahedron | Octahedron • Cube | Demicube | Dodecahedron • Icosahedron | ||||||||
| Uniform 4-polytope | 5-cell | 16-cell • Tesseract | Demitesseract | 24-cell | 120-cell • 600-cell | |||||||
| Uniform 5-polytope | 5-simplex | 5-orthoplex • 5-cube | 5-demicube | |||||||||
| Uniform 6-polytope | 6-simplex | 6-orthoplex • 6-cube | 6-demicube | 122 • 221 | ||||||||
| Uniform 7-polytope | 7-simplex | 7-orthoplex • 7-cube | 7-demicube | 132 • 231 • 321 | ||||||||
| Uniform 8-polytope | 8-simplex | 8-orthoplex • 8-cube | 8-demicube | 142 • 241 • 421 | ||||||||
| Uniform 9-polytope | 9-simplex | 9-orthoplex • 9-cube | 9-demicube | |||||||||
| Uniform 10-polytope | 10-simplex | 10-orthoplex • 10-cube | 10-demicube | |||||||||
| Uniform n-polytope | n-simplex | n-orthoplex • n-cube | n-demicube | 1k2 • 2k1 • k21 | n-pentagonal polytope | |||||||
| Topics: Polytope families • Regular polytope • List of regular polytopes and compounds | ||||||||||||