Standard Model

The Standard Model of particle physics is the theory describing three of the four known fundamental forces (the electromagnetic, weak, and strong interactions, and not including the gravitational force) in the universe, as well as classifying all known elementary particles. It was developed in stages throughout the latter half of the 20th century, through the work of many scientists around the world,[1] with the current formulation being finalized in the mid-1970s upon experimental confirmation of the existence of quarks. Since then, confirmation of the top quark (1995), the tau neutrino (2000), and the Higgs boson (2012) have added further credence to the Standard Model. In addition, the Standard Model has predicted various properties of weak neutral currents and the W and Z bosons with great accuracy.

This article is about a non-mathematical general overview of the Standard Model of particle physics. For a mathematical description, see Standard Model (mathematical formulation). For other uses, see Standard model (disambiguation).

Although the Standard Model is believed to be theoretically self-consistent[2] and has demonstrated huge successes in providing experimental predictions, it leaves some phenomena unexplained and falls short of being a complete theory of fundamental interactions. It does not fully explain baryon asymmetry, incorporate the full theory of gravitation[3] as described by general relativity, or account for the accelerating expansion of the Universe as possibly described by dark energy. The model does not contain any viable dark matter particle that possesses all of the required properties deduced from observational cosmology. It also does not incorporate neutrino oscillations and their non-zero masses.

The development of the Standard Model was driven by theoretical and experimental particle physicists alike. For theorists, the Standard Model is a paradigm of a quantum field theory, which exhibits a wide range of phenomena including spontaneous symmetry breaking, anomalies and non-perturbative behavior. It is used as a basis for building more exotic models that incorporate hypothetical particles, extra dimensions, and elaborate symmetries (such as supersymmetry) in an attempt to explain experimental results at variance with the Standard Model, such as the existence of dark matter and neutrino oscillations.

Historical background

See also: History of quantum field theory and History of subatomic physics

In 1954, Chen Ning Yang and Robert Mills extended the concept of gauge theory for abelian groups, e.g. quantum electrodynamics, to nonabelian groups to provide an explanation for strong interactions.[4] In 1961, Sheldon Glashow combined the electromagnetic and weak interactions.[5] In 1967 Steven Weinberg[6] and Abdus Salam[7] incorporated the Higgs mechanism[8][9][10] into Glashow's electroweak interaction, giving it its modern form.

The Higgs mechanism is believed to give rise to the masses of all the elementary particles in the Standard Model. This includes the masses of the W and Z bosons, and the masses of the fermions, i.e. the quarks and leptons.

After the neutral weak currents caused by Z boson exchange were discovered at CERN in 1973,[11][12][13][14] the electroweak theory became widely accepted and Glashow, Salam, and Weinberg shared the 1979 Nobel Prize in Physics for discovering it. The W^± and Z⁰ bosons were discovered experimentally in 1983; and the ratio of their masses was found to be as the Standard Model predicted.[15]

The theory of the strong interaction (i.e. quantum chromodynamics, QCD), to which many contributed, acquired its modern form in 1973–74 when asymptotic freedom was proposed[16][17] (a development which made QCD the main focus of theoretical research)[18] and experiments confirmed that the hadrons were composed of fractionally charged quarks.[19][20]

The term "Standard Model" was first coined by Abraham Pais and Sam Treiman in 1975, with reference to the electroweak theory with four quarks.[21]

Overview

At present, matter and energy are best understood in terms of the kinematics and interactions of elementary particles. To date, physics has reduced the laws governing the behavior and interaction of all known forms of matter and energy to a small set of fundamental laws and theories. A major goal of physics is to find the "common ground" that would unite all of these theories into one integrated theory of everything, of which all the other known laws would be special cases, and from which the behavior of all matter and energy could be derived (at least in principle).[22]

Particle content

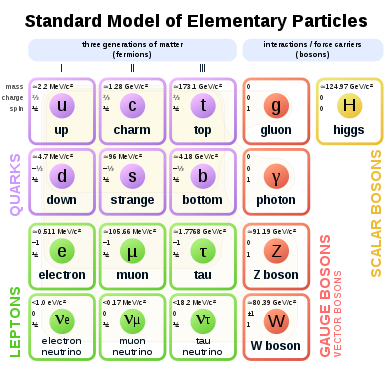
The Standard Model includes members of several classes of elementary particles, which in turn can be distinguished by other characteristics, such as color charge.

All particles can be summarized as follows:

Elementary particles

Elementary fermionsHalf-integer spinObey the Fermi–Dirac statistics

Elementary bosonsInteger spinObey the Bose–Einstein statistics

Quarks and antiquarksSpin = 1/2Have color chargeParticipate in strong interactions

Leptons and antileptonsSpin = 1/2No color chargeElectroweak interactions

Gauge bosonsSpin = 1Force carriers

Scalar bosonsSpin = 0

Three Generations Up (u),     Down (d) Charm (c),     Strange (s) Top (t),     Bottom (b)

Three Generations Electron ( e^− ),^[†]     Electron neutrino ( ν e) Muon ( μ^− ),     Muon neutrino ( ν μ) Tau ( τ^− ),     Tau neutrino ( ν τ)

Four kinds (four fundamental interactions) Photon ( γ , electromagnetic interaction) W and Z bosons ( W^+ , W^− , Z , weak interaction) Eight types of gluons ( g , strong interaction)

Unique Higgs boson ( H^0 )

Notes:
[†] An anti-electron (
e⁺
) is conventionally called a “positron”.

Fermions

Summary of interactions between particles described by the Standard Model

The Standard Model includes 12 elementary particles of spin ​¹⁄₂, known as fermions. According to the spin–statistics theorem, fermions respect the Pauli exclusion principle. Each fermion has a corresponding antiparticle.

Extended breakdown of particle interactions in the Standard Model if the hypothetical graviton were to be included.

Fermions are classified according to how they interact (or equivalently, by what charges they carry). There are six quarks (up, down, charm, strange, top, bottom), and six leptons (electron, electron neutrino, muon, muon neutrino, tau, tau neutrino). Each class is divided into pairs of particles that exhibit a similar physical behavior called a generation (see the table).

The defining property of quarks is that they carry color charge, and hence interact via the strong interaction. The phenomenon of color confinement results in quarks being very strongly bound to one another, forming color-neutral composite particles called hadrons that contain either a quark and an antiquark (mesons) or three quarks (baryons). The lightest baryons are the proton and the neutron. Quarks also carry electric charge and weak isospin. Hence they interact with other fermions via electromagnetism and the weak interaction. The remaining six fermions do not carry color charge and are called leptons. The three neutrinos do not carry electric charge either, so their motion is directly influenced only by the weak nuclear force, which makes them notoriously difficult to detect. By contrast, by virtue of carrying an electric charge, the electron, muon, and tau all interact electromagnetically.

Each member of a generation has greater mass than the corresponding particles of lower generations. The first-generation charged particles do not decay, hence all ordinary (baryonic) matter is made of such particles. Specifically, all atoms consist of electrons orbiting around atomic nuclei, ultimately constituted of up and down quarks. On the other hand, second- and third-generation charged particles decay with very short half-lives and are observed only in very high-energy environments. Neutrinos of all generations also do not decay and pervade the universe, but rarely interact with baryonic matter.

Gauge bosons

The above interactions form the basis of the standard model. Feynman diagrams in the standard model are built from these vertices. Modifications involving Higgs boson interactions and neutrino oscillations are omitted. The charge of the W bosons is dictated by the fermions they interact with; the conjugate of each listed vertex (i.e. reversing the direction of arrows) is also allowed.

In the Standard Model, gauge bosons are defined as force carriers that mediate the strong, weak, and electromagnetic fundamental interactions.

Interactions in physics are the ways that particles influence other particles. At a macroscopic level, electromagnetism allows particles to interact with one another via electric and magnetic fields, and gravitation allows particles with mass to attract one another in accordance with Einstein's theory of general relativity. The Standard Model explains such forces as resulting from matter particles exchanging other particles, generally referred to as force mediating particles. When a force-mediating particle is exchanged, the effect at a macroscopic level is equivalent to a force influencing both of them, and the particle is therefore said to have mediated (i.e., been the agent of) that force. The Feynman diagram calculations, which are a graphical representation of the perturbation theory approximation, invoke "force mediating particles", and when applied to analyze high-energy scattering experiments are in reasonable agreement with the data. However, perturbation theory (and with it the concept of a "force-mediating particle") fails in other situations. These include low-energy quantum chromodynamics, bound states, and solitons.

The gauge bosons of the Standard Model all have spin (as do matter particles). The value of the spin is 1, making them bosons. As a result, they do not follow the Pauli exclusion principle that constrains fermions: thus bosons (e.g. photons) do not have a theoretical limit on their spatial density (number per volume). The types of gauge bosons are described below.

• Photons mediate the electromagnetic force between electrically charged particles. The photon is massless and is well-described by the theory of quantum electrodynamics.
• The
  W⁺
  ,
  W⁻
  , and
  Z
  gauge bosons mediate the weak interactions between particles of different flavors (all quarks and leptons). They are massive, with the
  Z
  being more massive than the
  W^±
  . The weak interactions involving the
  W^±
  act only on left-handed particles and right-handed antiparticles. The
  W^±
  carries an electric charge of +1 and −1 and couples to the electromagnetic interaction. The electrically neutral
  Z
  boson interacts with both left-handed particles and antiparticles. These three gauge bosons along with the photons are grouped together, as collectively mediating the electroweak interaction.
• The eight gluons mediate the strong interactions between color charged particles (the quarks). Gluons are massless. The eightfold multiplicity of gluons is labeled by a combination of color and anticolor charge (e.g. red–antigreen).[note 1] Because gluons have an effective color charge, they can also interact among themselves. Gluons and their interactions are described by the theory of quantum chromodynamics.

The interactions between all the particles described by the Standard Model are summarized by the diagrams on the right of this section.

Higgs boson

Main article: Higgs boson

The Higgs particle is a massive scalar elementary particle theorized by Peter Higgs in 1964, when he showed that Goldstone's 1962 theorem (generic continuous symmetry, which is spontaneously broken) provides a third polarisation of a massive vector field. Hence, Goldstone's original scalar doublet, the massive spin-zero particle, was proposed as the Higgs boson, and is a key building block in the Standard Model.[8][9][10][23] It has no intrinsic spin, and for that reason is classified as a boson (like the gauge bosons, which have integer spin).

The Higgs boson plays a unique role in the Standard Model, by explaining why the other elementary particles, except the photon and gluon, are massive. In particular, the Higgs boson explains why the photon has no mass, while the W and Z bosons are very heavy. Elementary-particle masses, and the differences between electromagnetism (mediated by the photon) and the weak force (mediated by the W and Z bosons), are critical to many aspects of the structure of microscopic (and hence macroscopic) matter. In electroweak theory, the Higgs boson generates the masses of the leptons (electron, muon, and tau) and quarks. As the Higgs boson is massive, it must interact with itself.

Because the Higgs boson is a very massive particle and also decays almost immediately when created, only a very high-energy particle accelerator can observe and record it. Experiments to confirm and determine the nature of the Higgs boson using the Large Hadron Collider (LHC) at CERN began in early 2010 and were performed at Fermilab's Tevatron until its closure in late 2011. Mathematical consistency of the Standard Model requires that any mechanism capable of generating the masses of elementary particles becomes visible at energies above 1.4 TeV;[24] therefore, the LHC (designed to collide two 7 TeV proton beams) was built to answer the question of whether the Higgs boson actually exists.[25]

On 4 July 2012, two of the experiments at the LHC (ATLAS and CMS) both reported independently that they found a new particle with a mass of about 125 GeV/c² (about 133 proton masses, on the order of 10×10⁻²⁵ kg), which is "consistent with the Higgs boson".[26][27][28][29][30][31] On 13 March 2013, it was confirmed to be the searched-for Higgs boson.[32][33]

Theoretical aspects

Construction of the Standard Model Lagrangian

Parameters of the Standard Model
Symbol	Description	Renormalization scheme (point)	Value
me	Electron mass		511 keV
mμ	Muon mass		105.7 MeV
mτ	Tau mass		1.78 GeV
mu	Up quark mass	μMS = 2 GeV	1.9 MeV
md	Down quark mass	μMS = 2 GeV	4.4 MeV
ms	Strange quark mass	μMS = 2 GeV	87 MeV
mc	Charm quark mass	μMS = mc	1.32 GeV
mb	Bottom quark mass	μMS = mb	4.24 GeV
mt	Top quark mass	On shell scheme	173.5 GeV
θ12	CKM 12-mixing angle		13.1°
θ23	CKM 23-mixing angle		2.4°
θ13	CKM 13-mixing angle		0.2°
δ	CKM CP violation Phase		0.995
g1 or g'	U(1) gauge coupling	μMS = mZ	0.357
g2 or g	SU(2) gauge coupling	μMS = mZ	0.652
g3 or gs	SU(3) gauge coupling	μMS = mZ	1.221
θQCD	QCD vacuum angle		~0
v	Higgs vacuum expectation value		246 GeV
mH	Higgs mass		125.09±0.24 GeV

Technically, quantum field theory provides the mathematical framework for the Standard Model, in which a Lagrangian controls the dynamics and kinematics of the theory. Each kind of particle is described in terms of a dynamical field that pervades space-time. The construction of the Standard Model proceeds following the modern method of constructing most field theories: by first postulating a set of symmetries of the system, and then by writing down the most general renormalizable Lagrangian from its particle (field) content that observes these symmetries.

The global Poincaré symmetry is postulated for all relativistic quantum field theories. It consists of the familiar translational symmetry, rotational symmetry and the inertial reference frame invariance central to the theory of special relativity. The local SU(3)×SU(2)×U(1) gauge symmetry is an internal symmetry that essentially defines the Standard Model. Roughly, the three factors of the gauge symmetry give rise to the three fundamental interactions. The fields fall into different representations of the various symmetry groups of the Standard Model (see table). Upon writing the most general Lagrangian, one finds that the dynamics depends on 19 parameters, whose numerical values are established by experiment. The parameters are summarized in the table (made visible by clicking "show") above (note: the Higgs mass is at 125 GeV, the Higgs self-coupling strength λ ~ ​¹⁄₈).

Quantum chromodynamics sector

Main article: Quantum chromodynamics

The quantum chromodynamics (QCD) sector defines the interactions between quarks and gluons, which is a Yang–Mills gauge theory with SU(3) symmetry, generated by T^a. Since leptons do not interact with gluons, they are not affected by this sector. The Dirac Lagrangian of the quarks coupled to the gluon fields is given by

${\displaystyle {\mathcal {L}}_{\text{QCD}}=\sum _{\psi }{\overline {\psi }}_{i}\left(i\gamma ^{\mu }(\partial _{\mu }\delta _{ij}-ig_{s}G_{\mu }^{a}T_{ij}^{a})\right)\psi _{j}-{\frac {1}{4}}G_{\mu \nu }^{a}G_{a}^{\mu \nu },}$

where

ψ
_i is the Dirac spinor of the quark field, where i = {r, g, b} represents color,

γ^μ are the Dirac matrices,

G^a
_μ is the 8-component (${\displaystyle a=1,2,\dots ,8}$) SU(3) gauge field,

T^a
_ij are the 3 × 3 Gell-Mann matrices, generators of the SU(3) color group,

G^a
_μν represents the gluon field strength tensor,

g_s is the strong coupling constant.

Electroweak sector

Main article: Electroweak interaction

The electroweak sector is a Yang–Mills gauge theory with the symmetry group U(1) × SU(2)_L,

${\displaystyle {\mathcal {L}}_{\text{EW}}=\sum _{\psi }{\bar {\psi }}\gamma ^{\mu }\left(i\partial _{\mu }-g'{\tfrac {1}{2}}Y_{\text{W}}B_{\mu }-g{\tfrac {1}{2}}{\vec {\tau }}_{\text{L}}{\vec {W}}_{\mu }\right)\psi -{\tfrac {1}{4}}W_{a}^{\mu \nu }W_{\mu \nu }^{a}-{\tfrac {1}{4}}B^{\mu \nu }B_{\mu \nu },}$

where

B_μ is the U(1) gauge field,

Y_W is the weak hypercharge – the generator of the U(1) group,

W→_μ is the 3-component SU(2) gauge field,

τ_L→ are the Pauli matrices – infinitesimal generators of the SU(2) group – with subscript L to indicate that they only act on left-chiral fermions,

g' and g are the U(1) and SU(2) coupling constants respectively,

${\displaystyle W^{a\mu \nu }}$ (${\displaystyle a=1,2,3}$) and ${\displaystyle B^{\mu \nu }}$ are the field strength tensors for the weak isospin and weak hypercharge fields.

Notice that the addition of fermion mass terms into the electroweak lagrangian is forbidden, since terms of the form ${\displaystyle m{\overline {\psi }}\psi }$ do not respect U(1) × SU(2)_L gauge invariance. Neither is it possible to add explicit mass terms for the U(1) and SU(2) gauge fields. The Higgs mechanism is responsible for the generation of the gauge boson masses, and the fermion masses result from Yukawa-type interactions with the Higgs field.

Higgs sector

Main article: Higgs mechanism

In the Standard Model, the Higgs field is a complex scalar of the group SU(2)_L:

${\displaystyle \varphi ={\frac {1}{\sqrt {2}}}\left({\begin{array}{c}\varphi ^{+}\\\varphi ^{0}\end{array}}\right),}$

where the superscripts + and 0 indicate the electric charge (Q) of the components. The weak hypercharge (Y_W) of both components is 1.

Before symmetry breaking, the Higgs Lagrangian is

${\displaystyle {\mathcal {L}}_{\text{H}}=\varphi ^{\dagger }\left(\partial ^{\mu }-{\frac {i}{2}}\left(g'Y_{\text{W}}B^{\mu }+g{\vec {\tau }}{\vec {W}}^{\mu }\right)\right)\left(\partial _{\mu }+{\frac {i}{2}}\left(g'Y_{\text{W}}B_{\mu }+g{\vec {\tau }}{\vec {W}}_{\mu }\right)\right)\varphi -{\frac {\lambda ^{2}}{4}}\left(\varphi ^{\dagger }\varphi -v^{2}\right)^{2},}$

which up to a divergence term, (i.e. after partial integration) can also be written as

${\displaystyle {\mathcal {L}}_{\text{H}}=\left|\left(\partial _{\mu }+{\frac {i}{2}}\left(g'Y_{\text{W}}B_{\mu }+g{\vec {\tau }}{\vec {W}}_{\mu }\right)\right)\varphi \right|^{2}-{\frac {\lambda ^{2}}{4}}\left(\varphi ^{\dagger }\varphi -v^{2}\right)^{2}.}$

Yukawa sector

The Yukawa interaction terms are

${\displaystyle {\mathcal {L}}_{\text{Yukawa}}={\overline {U}}_{L}G_{u}U_{R}\varphi ^{0}-{\overline {D}}_{L}G_{u}U_{R}\varphi ^{-}+{\overline {U}}_{L}G_{d}D_{R}\varphi ^{+}+{\overline {D}}_{L}G_{d}D_{R}\varphi ^{0}+hc,}$

where G_u,d are 3 × 3 matrices of Yukawa couplings, with the ij term giving the coupling of the generations i and j.

Fundamental interactions

Main article: Fundamental interaction

The Standard Model describes three of the four fundamental interactions in nature; only gravity remains unexplained. In the Standard Model, an interaction is described as an exchange of bosons between the objects affected, such as a photon for the electromagnetic force and a gluon for the strong interaction. Those particles are called force carriers or messenger particles.[34]

The four fundamental interactions of nature[35]

Property/Interaction	Gravitation	Electroweak		Strong
		Weak	Electromagnetic	Fundamental	Residual
Mediating particles	Not yet observed (Graviton hypothesised)	W^+, W^− and Z^0	γ (photon)	Gluons	π, ρ and ω mesons
Affected particles	All particles	Left-handed fermions	Electrically charged	Quarks, gluons	Hadrons
Acts on	Mass, energy	Flavor	Electric charge	Color charge
Bound states formed	Planets, stars, galaxies, galaxy groups	n/a	Atoms, molecules	Hadrons	Atomic nuclei
Strength at the scale of quarks (relative to electromagnetism)	10^−41 (predicted)	10^−4	1	60	Not applicable to quarks
Strength at the scale of protons/neutrons (relative to electromagnetism)	10^−36 (predicted)	10^−7	1	Not applicable to hadrons	20

Tests and predictions

The Standard Model (SM) predicted the existence of the W and Z bosons, gluon, and the top and charm quarks and predicted many of their properties before these particles were observed. The predictions were experimentally confirmed with good precision.[36]

The SM also predicted the existence of the Higgs boson, found in 2012 at the Large Hadron Collider, as the last particle of the SM.[37]

Challenges

See also: Physics beyond the Standard Model

Unsolved problem in physics: What gives rise to the Standard Model of particle physics? Why do particle masses and coupling constants have the values that we measure? Why are there three generations of particles? Why is there more matter than antimatter in the universe? Where does Dark Matter fit into the model? Does it even consist of one or more new particles? (more unsolved problems in physics)

Self-consistency of the Standard Model (currently formulated as a non-abelian gauge theory quantized through path-integrals) has not been mathematically proven. While regularized versions useful for approximate computations (for example lattice gauge theory) exist, it is not known whether they converge (in the sense of S-matrix elements) in the limit that the regulator is removed. A key question related to the consistency is the Yang–Mills existence and mass gap problem.

Experiments indicate that neutrinos have mass, which the classic Standard Model did not allow.[38] To accommodate this finding, the classic Standard Model can be modified to include neutrino mass.

If one insists on using only Standard Model particles, this can be achieved by adding a non-renormalizable interaction of leptons with the Higgs boson.[39] On a fundamental level, such an interaction emerges in the seesaw mechanism where heavy right-handed neutrinos are added to the theory. This is natural in the left-right symmetric extension of the Standard Model[40][41] and in certain grand unified theories.[42] As long as new physics appears below or around 10¹⁴ GeV, the neutrino masses can be of the right order of magnitude.

Theoretical and experimental research has attempted to extend the Standard Model into a Unified field theory or a Theory of everything, a complete theory explaining all physical phenomena including constants. Inadequacies of the Standard Model that motivate such research include:

• The model does not explain gravitation, although physical confirmation of a theoretical particle known as a graviton would account for it to a degree. Though it addresses strong and electroweak interactions, the Standard Model does not consistently explain the canonical theory of gravitation, general relativity, in terms of quantum field theory. The reason for this is, among other things, that quantum field theories of gravity generally break down before reaching the Planck scale. As a consequence, we have no reliable theory for the very early universe.
• Some physicists consider it to be ad hoc and inelegant, requiring 19 numerical constants whose values are unrelated and arbitrary.[43] Although the Standard Model, as it now stands, can explain why neutrinos have masses, the specifics of neutrino mass are still unclear. It is believed that explaining neutrino mass will require an additional 7 or 8 constants, which are also arbitrary parameters.[44]
• The Higgs mechanism gives rise to the hierarchy problem if some new physics (coupled to the Higgs) is present at high energy scales. In these cases, in order for the weak scale to be much smaller than the Planck scale, severe fine tuning of the parameters is required; there are, however, other scenarios that include quantum gravity in which such fine tuning can be avoided.[45] There are also issues of quantum triviality, which suggests that it may not be possible to create a consistent quantum field theory involving elementary scalar particles.[46]
• The model is inconsistent with the emerging Lambda-CDM model of cosmology. Contentions include the absence of an explanation in the Standard Model of particle physics for the observed amount of cold dark matter (CDM) and its contributions to dark energy, which are many orders of magnitude too large. It is also difficult to accommodate the observed predominance of matter over antimatter (matter/antimatter asymmetry). The isotropy and homogeneity of the visible universe over large distances seems to require a mechanism like cosmic inflation, which would also constitute an extension of the Standard Model.

Currently, no proposed Theory of Everything has been widely accepted or verified.

See also

• Yang–Mills theory
• Fundamental interaction:
  • Quantum electrodynamics
  • Strong interaction: Color charge, Quantum chromodynamics, Quark model
  • Weak interaction: Electroweak interaction, Fermi's interaction, Weak hypercharge, Weak isospin
• Gauge theory: Introduction to gauge theory
• Generation
• Higgs mechanism: Higgs boson, Alternatives to the Standard Higgs Model
• Lagrangian
• Open questions: CP violation, Neutrino masses, QCD matter, Quantum triviality
• Quantum field theory
• Standard Model: Mathematical formulation of, Physics beyond the Standard Model
• Electron electric dipole moment

Notes

1. Technically, there are nine such color–anticolor combinations. However, one of these is a color-symmetric combination that can be constructed out of a linear superposition, reducing the count to eight.

References

1. R. Oerter (2006). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics (Kindle ed.). Penguin Group. p. 2. ISBN 978-0-13-236678-6.
2. In fact, there are mathematical issues regarding quantum field theories still under debate (see e.g. Landau pole), but the predictions extracted from the Standard Model by current methods applicable to current experiments are all self-consistent. For a further discussion see e.g. Chapter 25 of R. Mann (2010). An Introduction to Particle Physics and the Standard Model. CRC Press. ISBN 978-1-4200-8298-2.
3. Sean Carroll, Ph.D., Caltech, 2007, The Teaching Company, Dark Matter, Dark Energy: The Dark Side of the Universe, Guidebook Part 2 page 59, Accessed Oct. 7, 2013, "...Standard Model of Particle Physics: The modern theory of elementary particles and their interactions ... It does not, strictly speaking, include gravity, although it's often convenient to include gravitons among the known particles of nature..."
4. Yang, C. N.; Mills, R. (1954). "Conservation of Isotopic Spin and Isotopic Gauge Invariance". Physical Review. 96 (1): 191–195. Bibcode:1954PhRv...96..191Y. doi:10.1103/PhysRev.96.191.
5. S.L. Glashow (1961). "Partial-symmetries of weak interactions". Nuclear Physics. 22 (4): 579–588. Bibcode:1961NucPh..22..579G. doi:10.1016/0029-5582(61)90469-2.
6. S. Weinberg (1967). "A Model of Leptons". Physical Review Letters. 19 (21): 1264–1266. Bibcode:1967PhRvL..19.1264W. doi:10.1103/PhysRevLett.19.1264.
7. A. Salam (1968). N. Svartholm (ed.). Elementary Particle Physics: Relativistic Groups and Analyticity. Eighth Nobel Symposium. Stockholm: Almquvist and Wiksell. p. 367.
8. F. Englert; R. Brout (1964). "Broken Symmetry and the Mass of Gauge Vector Mesons". Physical Review Letters. 13 (9): 321–323. Bibcode:1964PhRvL..13..321E. doi:10.1103/PhysRevLett.13.321.
9. P.W. Higgs (1964). "Broken Symmetries and the Masses of Gauge Bosons". Physical Review Letters. 13 (16): 508–509. Bibcode:1964PhRvL..13..508H. doi:10.1103/PhysRevLett.13.508.
10. G.S. Guralnik; C.R. Hagen; T.W.B. Kibble (1964). "Global Conservation Laws and Massless Particles". Physical Review Letters. 13 (20): 585–587. Bibcode:1964PhRvL..13..585G. doi:10.1103/PhysRevLett.13.585.
11. F.J. Hasert; et al. (1973). "Search for elastic muon-neutrino electron scattering". Physics Letters B. 46 (1): 121. Bibcode:1973PhLB...46..121H. doi:10.1016/0370-2693(73)90494-2.
12. F.J. Hasert; et al. (1973). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Physics Letters B. 46 (1): 138. Bibcode:1973PhLB...46..138H. doi:10.1016/0370-2693(73)90499-1.
13. F.J. Hasert; et al. (1974). "Observation of neutrino-like interactions without muon or electron in the Gargamelle neutrino experiment". Nuclear Physics B. 73 (1): 1. Bibcode:1974NuPhB..73....1H. doi:10.1016/0550-3213(74)90038-8.
14. D. Haidt (4 October 2004). "The discovery of the weak neutral currents". CERN Courier. Retrieved 8 May 2008.
15. Gaillard, Mary K.; Grannis, Paul D.; Sciulli, Frank J. (January 1999). "The Standard Model of Particle Physics". Reviews of Modern Physics. 71 (2): S96–S111. arXiv:hep-ph/9812285. Bibcode:1999RvMPS..71...96G. doi:10.1103/RevModPhys.71.S96.
16. D.J. Gross; F. Wilczek (1973). "Ultraviolet behavior of non-abelian gauge theories". Physical Review Letters. 30 (26): 1343–1346. Bibcode:1973PhRvL..30.1343G. doi:10.1103/PhysRevLett.30.1343.
17. H.D. Politzer (1973). "Reliable perturbative results for strong interactions" (PDF). Physical Review Letters. 30 (26): 1346–1349. Bibcode:1973PhRvL..30.1346P. doi:10.1103/PhysRevLett.30.1346.
18. Dean Rickles (2014). A Brief History of String Theory: From Dual Models to M-Theory. Springer, p. 11 n. 22.
19. Aubert, J.; et al. (1974). "Experimental Observation of a Heavy Particle J". Physical Review Letters. 33 (23): 1404–1406. Bibcode:1974PhRvL..33.1404A. doi:10.1103/PhysRevLett.33.1404.
20. Augustin, J.; et al. (1974). "Discovery of a Narrow Resonance in e⁺e⁻ Annihilation". Physical Review Letters. 33 (23): 1406–1408. Bibcode:1974PhRvL..33.1406A. doi:10.1103/PhysRevLett.33.1406.
21. Cao, Tian Yu. Conceptual developments of 20th century field theories. Cambridge University Press, 1998, p. 320.
22. "Details can be worked out if the situation is simple enough for us to make an approximation, which is almost never, but often we can understand more or less what is happening." from The Feynman Lectures on Physics, Vol 1. pp. 2–7
23. G.S. Guralnik (2009). "The History of the Guralnik, Hagen and Kibble development of the Theory of Spontaneous Symmetry Breaking and Gauge Particles". International Journal of Modern Physics A. 24 (14): 2601–2627. arXiv:0907.3466. Bibcode:2009IJMPA..24.2601G. doi:10.1142/S0217751X09045431.
24. B.W. Lee; C. Quigg; H.B. Thacker (1977). "Weak interactions at very high energies: The role of the Higgs-boson mass". Physical Review D. 16 (5): 1519–1531. Bibcode:1977PhRvD..16.1519L. doi:10.1103/PhysRevD.16.1519.
25. "Huge $10 billion collider resumes hunt for 'God particle'". CNN. 11 November 2009. Retrieved 4 May 2010.
26. M. Strassler (10 July 2012). "Higgs Discovery: Is it a Higgs?". Retrieved 6 August 2013.
27. "CERN experiments observe particle consistent with long-sought Higgs boson". CERN. 4 July 2012. Retrieved 12 November 2016.
28. "Observation of a New Particle with a Mass of 125 GeV". CERN. 4 July 2012. Retrieved 5 July 2012.
29. "ATLAS Experiment". ATLAS. 4 July 2012. Retrieved 13 June 2017.
30. "Confirmed: CERN discovers new particle likely to be the Higgs boson". YouTube. Russia Today. 4 July 2012. Retrieved 6 August 2013.
31. D. Overbye (4 July 2012). "A New Particle Could Be Physics' Holy Grail". The New York Times. Retrieved 4 July 2012.
32. "New results indicate that particle discovered at CERN is a Higgs boson". CERN. 14 March 2013. Retrieved 14 June 2020.
33. "LHC experiments delve deeper into precision". CERN. 11 July 2017. Retrieved 23 July 2017.
34. http://home.web.cern.ch/about/physics/standard-model Official CERN website
35. "Standard Model of Particles and Interactions". jhu.edu. Johns Hopkins University. Archived from the original on 4 March 2016. Retrieved 18 August 2016. .gif
36. Woithe, Julia; Wiener, Gerfried; Van der Veken, Frederik (2017). "Let's have a coffee with the Standard Model of particle physics!". Phys. Educ. 52 (3): 034001. Bibcode:2017PhyEd..52c4001W. doi:10.1088/1361-6552/aa5b25.
37. Altarelli, Guido (2014). "The Higgs and the Excessive Success of the Standard Model". arXiv:1407.2122 [hep-ph].
38. "Particle chameleon caught in the act of changing". CERN. 31 May 2010. Retrieved 12 November 2016.
39. S. Weinberg (1979). "Baryon and Lepton Nonconserving Processes". Physical Review Letters. 43 (21): 1566–1570. Bibcode:1979PhRvL..43.1566W. doi:10.1103/PhysRevLett.43.1566.
40. P. Minkowski (1977). "μ → e γ at a Rate of One Out of 10⁹ Muon Decays?". Physics Letters B. 67 (4): 421–428. Bibcode:1977PhLB...67..421M. doi:10.1016/0370-2693(77)90435-X.
41. R.N. Mohapatra; G. Senjanovic (1980). "Neutrino Mass and Spontaneous Parity Nonconservation". Physical Review Letters. 44 (14): 912–915. Bibcode:1980PhRvL..44..912M. doi:10.1103/PhysRevLett.44.912.
42. M. Gell-Mann, P. Ramond & R. Slansky (1979). F. van Nieuwenhuizen & D.Z. Freedman (eds.). Supergravity. North Holland. pp. 315–321. ISBN 978-0-444-85438-4.
43. A. Blumhofer; M. Hutter (1997). "Family Structure from Periodic Solutions of an Improved Gap Equation". Nuclear Physics. B484 (1): 80–96. arXiv:hep-ph/9605393. Bibcode:1997NuPhB.484...80B. doi:10.1016/S0550-3213(96)00644-X.
44. Strumia, Alessandro (2006). "Neutrino masses and mixings and...". arXiv:hep-ph/0606054.
45. Salvio, Alberto; Strumia, Alessandro (2018). "Agravity". Journal of High Energy Physics. 2014 (6): 080. arXiv:1403.4226. Bibcode:2014JHEP...06..080S. doi:10.1007/JHEP06(2014)080. PMC 6560704. PMID 31258400.
46. D.J.E. Callaway (1988). "Triviality Pursuit: Can Elementary Scalar Particles Exist?". Physics Reports. 167 (5): 241–320. Bibcode:1988PhR...167..241C. doi:10.1016/0370-1573(88)90008-7.

Further reading

• R. Oerter (2006). The Theory of Almost Everything: The Standard Model, the Unsung Triumph of Modern Physics. Plume.
• B.A. Schumm (2004). Deep Down Things: The Breathtaking Beauty of Particle Physics. Johns Hopkins University Press. ISBN 978-0-8018-7971-5.
• "The Standard Model of Particle Physics Interactive Graphic".

Introductory textbooks

• I. Aitchison; A. Hey (2003). Gauge Theories in Particle Physics: A Practical Introduction. Institute of Physics. ISBN 978-0-585-44550-2.
• W. Greiner; B. Müller (2000). Gauge Theory of Weak Interactions. Springer. ISBN 978-3-540-67672-0.
• G.D. Coughlan; J.E. Dodd; B.M. Gripaios (2006). The Ideas of Particle Physics: An Introduction for Scientists. Cambridge University Press.
• D.J. Griffiths (1987). Introduction to Elementary Particles. John Wiley & Sons. ISBN 978-0-471-60386-3.
• G.L. Kane (1987). Modern Elementary Particle Physics. Perseus Books. ISBN 978-0-201-11749-3.

Advanced textbooks

• T.P. Cheng; L.F. Li (2006). Gauge theory of elementary particle physics. Oxford University Press. ISBN 978-0-19-851961-4. Highlights the gauge theory aspects of the Standard Model.
• J.F. Donoghue; E. Golowich; B.R. Holstein (1994). Dynamics of the Standard Model. Cambridge University Press. ISBN 978-0-521-47652-2. Highlights dynamical and phenomenological aspects of the Standard Model.
• L. O'Raifeartaigh (1988). Group structure of gauge theories. Cambridge University Press. ISBN 978-0-521-34785-3.
• Nagashima, Yorikiyo (2013). Elementary Particle Physics: Foundations of the Standard Model, Volume 2. Wiley. ISBN 978-3-527-64890-0. 920 pages.
• Schwartz, Matthew D. (2014). Quantum Field Theory and the Standard Model. Cambridge University. ISBN 978-1-107-03473-0. 952 pages.
• Langacker, Paul (2009). The Standard Model and Beyond. CRC Press. ISBN 978-1-4200-7907-4. 670 pages. Highlights group-theoretical aspects of the Standard Model.

Journal articles

• E.S. Abers; B.W. Lee (1973). "Gauge theories". Physics Reports. 9 (1): 1–141. Bibcode:1973PhR.....9....1A. doi:10.1016/0370-1573(73)90027-6.
• M. Baak; et al. (2012). "The Electroweak Fit of the Standard Model after the Discovery of a New Boson at the LHC". The European Physical Journal C. 72 (11): 2205. arXiv:1209.2716. Bibcode:2012EPJC...72.2205B. doi:10.1140/epjc/s10052-012-2205-9.
• Y. Hayato; et al. (1999). "Search for Proton Decay through p → νK⁺ in a Large Water Cherenkov Detector". Physical Review Letters. 83 (8): 1529–1533. arXiv:hep-ex/9904020. Bibcode:1999PhRvL..83.1529H. doi:10.1103/PhysRevLett.83.1529.
• S.F. Novaes (2000). "Standard Model: An Introduction". arXiv:hep-ph/0001283.
• D.P. Roy (1999). "Basic Constituents of Matter and their Interactions – A Progress Report". arXiv:hep-ph/9912523.
• F. Wilczek (2004). "The Universe Is A Strange Place". Nuclear Physics B: Proceedings Supplements. 134: 3. arXiv:astro-ph/0401347. Bibcode:2004NuPhS.134....3W. doi:10.1016/j.nuclphysbps.2004.08.001.

External links

• "The Standard Model explained in Detail by CERN's John Ellis" omega tau podcast.
• "The Standard Model" on the CERN web site explains how the basic building blocks of matter interact, governed by four fundamental forces.
• Particle Physics: Standard Model, Leonard Susskind lectures (2010).
• "Standard Model" on YouTube