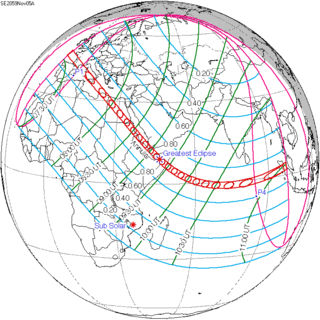
Solar eclipse of November 5, 2059

An annular solar eclipse will occur on Wednesday, November 5, 2059. A solar eclipse occurs when the Moon passes between Earth and the Sun, thereby totally or partly obscuring the image of the Sun for a viewer on Earth. An annular solar eclipse occurs when the Moon's apparent diameter is smaller than the Sun's, blocking most of the Sun's light and causing the Sun to look like an annulus (ring). An annular eclipse appears as a partial eclipse over a region of the Earth thousands of kilometres wide. The Sun will be 94% covered in a moderate annular eclipse, lasting 7 minutes exactly and covering a broad path up to 238 km wide.

Solar eclipse of November 5, 2059
Map
Type of eclipse
Nature	Annular
Gamma	0.4454
Magnitude	0.9417
Maximum eclipse
Duration	420 sec (7 m 0 s)
Coordinates	8.7°N 47.1°E / 8.7; 47.1
Max. width of band	238 km (148 mi)
Times (UTC)
Greatest eclipse	9:18:15
References
Saros	134 (46 of 71)
Catalog # (SE5000)	9641

Related eclipses

Solar eclipses 2059–2061

This eclipse is a member of a semester series. An eclipse in a semester series of solar eclipses repeats approximately every 177 days and 4 hours (a semester) at alternating nodes of the Moon's orbit.[1]

Solar eclipses 2059–2061
119	May 22, 2058 Partial	124	November 16, 2058 Partial
129	May 11, 2059 Total	134	November 5, 2059 Annular
139	April 30, 2060 Total	144	October 24, 2060 Annular
149	April 20, 2061 Total	154	October 13, 2061 Annular

Saros 134

It is a part of Saros cycle 134, repeating every 18 years, 11 days, containing 71 events. The series started with partial solar eclipse on June 22, 1248. It contains total eclipses from October 9, 1428 through December 24, 1554 and hybrid eclipses from January 3, 1573 through June 27, 1843, and annular eclipses from July 8, 1861 through May 21, 2384. The series ends at member 71 as a partial eclipse on August 6, 2510. The longest duration of totality was 1 minutes, 30 seconds on October 9, 1428. All eclipses in this series occurs at the Moon’s descending node.[2]

Series members 32–48 occur between 1801 and 2100:
32	33	34
June 6, 1807	June 16, 1825	June 27, 1843
35	36	37
July 8, 1861	July 19, 1879	July 29, 1897
38	39	40
August 10, 1915	August 21, 1933	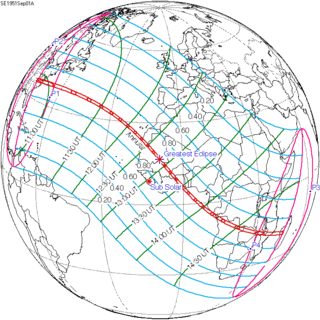September 1, 1951
41	42	43
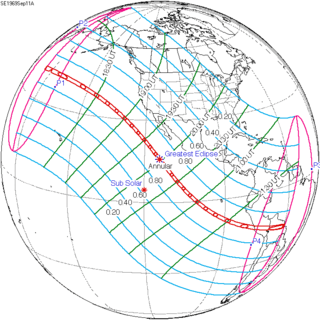September 11, 1969	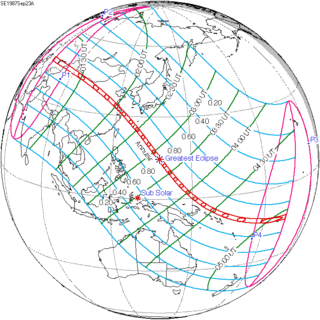September 23, 1987	October 3, 2005
44	45	46
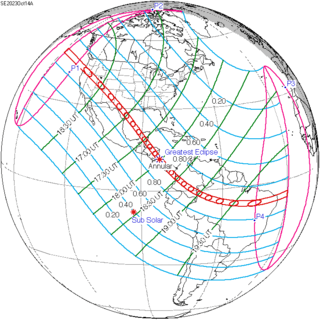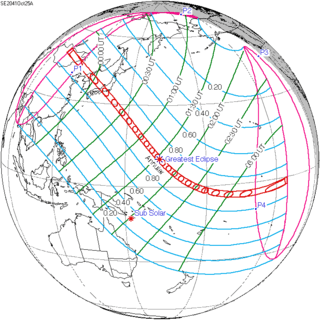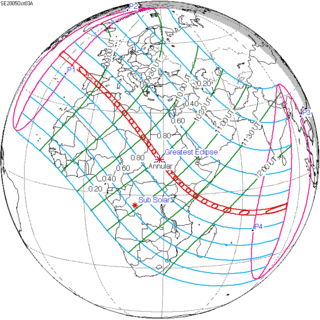
October 14, 2023	October 25, 2041	November 5, 2059
47	48
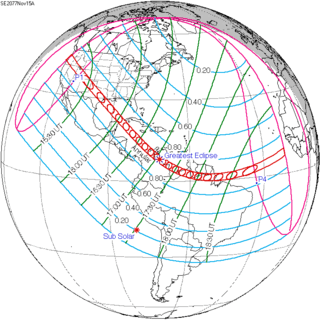November 15, 2077	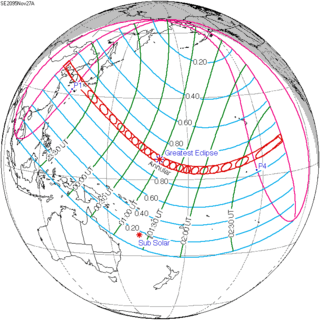November 27, 2095

Metonic cycle

The metonic series repeats eclipses every 19 years (6939.69 days), lasting about 5 cycles. Eclipses occur in nearly the same calendar date. In addition, the octon subseries repeats 1/5 of that or every 3.8 years (1387.94 days).

21 eclipse events between June 12, 2029 and June 12, 2105
June 11–12	March 30–31	January 16	November 4–5	August 23–24
118	120	122	124	126
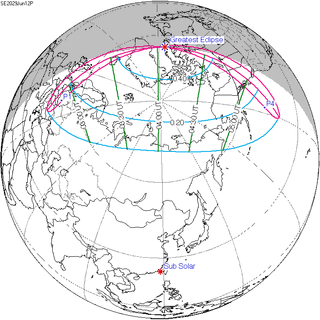June 12, 2029	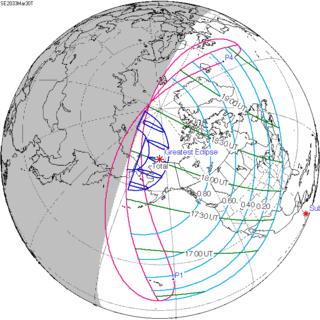March 30, 2033	January 16, 2037	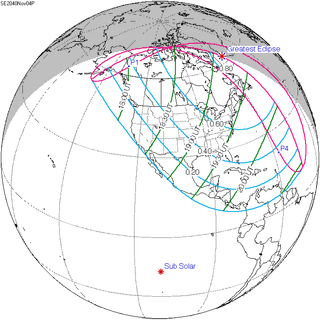November 4, 2040	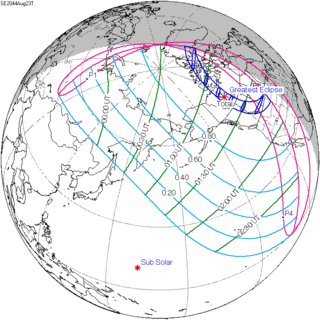August 23, 2044
128	130	132	134	136
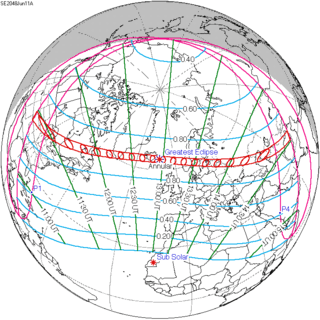June 11, 2048	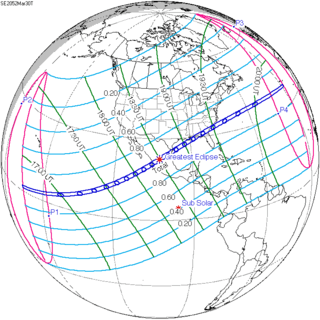March 30, 2052	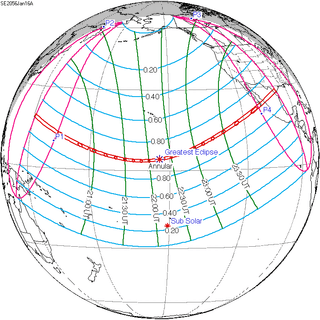January 16, 2056	November 5, 2059	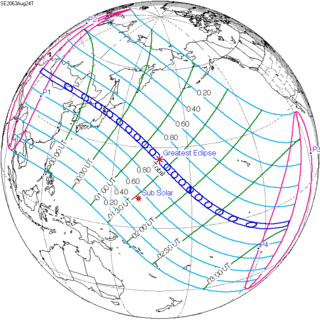August 24, 2063
138	140	142	144	146
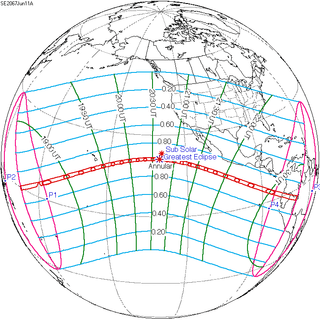June 11, 2067	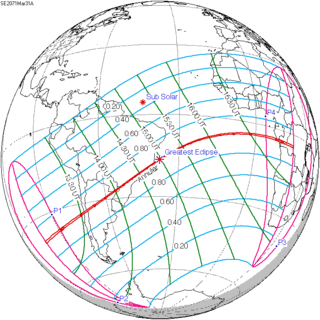March 31, 2071	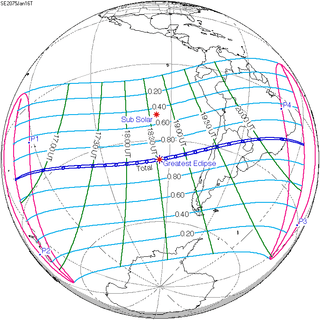January 16, 2075	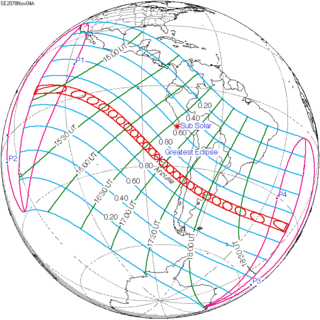November 4, 2078	August 24, 2082
148	150	152	154
June 11, 2086	March 31, 2090	January 16, 2094	November 4, 2097

References

1. van Gent, R.H. "Solar- and Lunar-Eclipse Predictions from Antiquity to the Present". A Catalogue of Eclipse Cycles. Utrecht University. Retrieved 6 October 2018.
2. http://eclipse.gsfc.nasa.gov/SEsaros/SEsaros134.html

External links

• http://eclipse.gsfc.nasa.gov/SEplot/SEplot2051/SE2059Nov05A.GIF