List of Wenninger polyhedron models

This is an indexed list of the uniform and stellated polyhedra from the book Polyhedron Models, by Magnus Wenninger.

The book was written as a guide book to building polyhedra as physical models. It includes templates of face elements for construction and helpful hints in building, and also brief descriptions on the theory behind these shapes. It contains the 75 nonprismatic uniform polyhedra, as well as 44 stellated forms of the convex regular and quasiregular polyhedra.

Models listed here can be cited as "Wenninger Model Number N", or W_N for brevity.

The polyhedra are grouped in 5 tables: Regular (1–5), Semiregular (6–18), regular star polyhedra (20–22,41), Stellations and compounds (19–66), and uniform star polyhedra (67–119). The four regular star polyhedra are listed twice because they belong to both the uniform polyhedra and stellation groupings.

Platonic solids (regular) W1 to W5

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol	Vertex figure and Schläfli symbol	Symmetry group	U#	K#	V	E	F	Faces by type
1	Tetrahedron		Tetrahedron		3|2 3	{3,3}	Td	U01	K06	4	6	4	4{3}
2	Octahedron		Hexahedron		4|2 3	{3,4}	Oh	U05	K10	6	12	8	8{3}
3	Hexahedron (Cube)		Octahedron		3|2 4	{4,3}	Oh	U06	K11	8	12	6	6{4}
4	Icosahedron		Dodecahedron		5|2 3	{3,5}	Ih	U22	K27	12	30	20	20{3}
5	Dodecahedron		Icosahedron		3|2 5	{5,3}	Ih	U23	K28	20	30	12	12{5}

Archimedean solids (Semiregular) W6 to W18

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol	Vertex figure	Symmetry group	U#	K#	V	E	F	Faces by type
6	Truncated tetrahedron		triakis tetrahedron		2 3|3	3.6.6	Td	U02	K07	12	18	8	4{3} + 4{6}
7	Truncated octahedron		tetrakis hexahedron		2 4|3	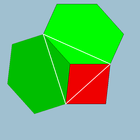4.6.6	Oh	U08	K13	24	36	24	6{4} + 8{6}
8	Truncated hexahedron		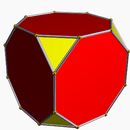triakis octahedron		2 3|4	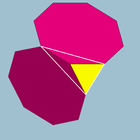3.8.8	Oh	U09	K14	24	36	14	8{3} + 6{8}
9	Truncated icosahedron		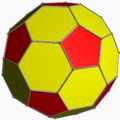pentakis dodecahedron		2 5|3	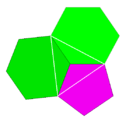5.6.6	Ih	U25	K30	60	90	32	12{5} + 20{6}
10	Truncated dodecahedron		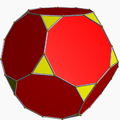triakis icosahedron		2 3|5	3.10.10	Ih	U26	K31	60	90	32	20{3} + 12{10}
11	Cuboctahedron		rhombic dodecahedron		2|3 4	3.4.3.4	Oh	U07	K12	12	24	14	8{3} + 6{4}
12	Icosidodecahedron		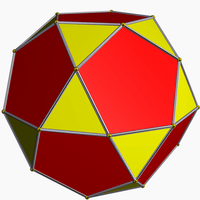rhombic triacontahedron		2|3 5	3.5.3.5	Ih	U24	K29	30	60	32	20{3} + 12{5}
13	Small rhombicuboctahedron		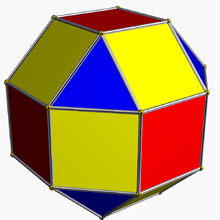deltoidal icositetrahedron		3 4|2	3.4.4.4	Oh	U10	K15	24	48	26	8{3}+(6+12){4}
14	Small rhombicosidodecahedron		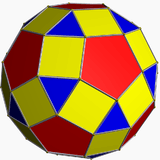deltoidal hexecontahedron		3 5|2	3.4.5.4	Ih	U27	K32	60	120	62	20{3} + 30{4} + 12{5}
15	Truncated cuboctahedron (Great rhombicuboctahedron)		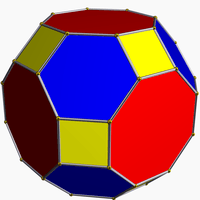disdyakis dodecahedron		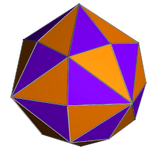2 3 4|	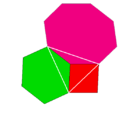4.6.8	Oh	U11	K16	48	72	26	12{4} + 8{6} + 6{8}
16	Truncated icosidodecahedron (Great rhombicosidodecahedron)		disdyakis triacontahedron		2 3 5|	4.6.10	Ih	U28	K33	120	180	62	30{4} + 20{6} + 12{10}
17	Snub cube		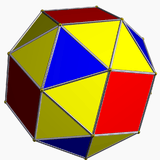pentagonal icositetrahedron		|2 3 4	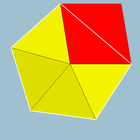3.3.3.3.4	O	U12	K17	24	60	38	(8 + 24){3} + 6{4}
18	Snub dodecahedron		pentagonal hexecontahedron		|2 3 5	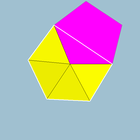3.3.3.3.5	I	U29	K34	60	150	92	(20 + 60){3} + 12{5}

Kepler–Poinsot polyhedra (Regular star polyhedra) W20, W21, W22 and W41

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol	Vertex figure and Schläfli symbol	Symmetry group	U#	K#	V	E	F	Faces by type
20	Small stellated dodecahedron		Great dodecahedron		5|2^5/2	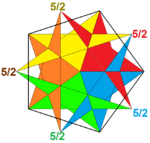{^5/2,5}	Ih	U34	K39	12	30	12	12{^5/2}
21	Great dodecahedron		Small stellated dodecahedron		^5/2|2 5	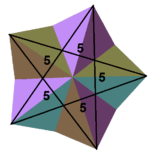{5,^5/2}	Ih	U35	K40	12	30	12	12{5}
22	Great stellated dodecahedron		Great icosahedron		3|2^5/2	{^5/2,3}	Ih	U52	K57	20	30	12	12{^5/2}
41	Great icosahedron (16th stellation of icosahedron)		Great stellated dodecahedron		^5/2|2 3	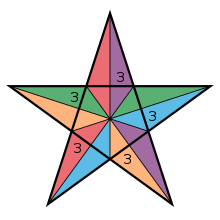{3,^5/2}	Ih	U53	K58	12	30	20	20{3}

Stellations: models W19 to W66

Stellations of octahedron

Index	Name	Symmetry group	Picture	Facets
2	Octahedron (regular)	Oh
19	Stellated octahedron (Compound of two tetrahedra)	Oh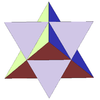

Stellations of dodecahedron

Index	Name	Symmetry group	Picture	Facets
5	Dodecahedron (regular)	Ih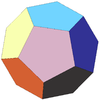
20	Small stellated dodecahedron (regular) (First stellation of dodecahedron)	Ih
21	Great dodecahedron (regular) (Second stellation of dodecahedron)	Ih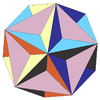
22	Great stellated dodecahedron (regular) (Third stellation of dodecahedron)	Ih

Stellations of icosahedron

Index	Name	Symmetry group	Picture	Facets
4	Icosahedron (regular)	Ih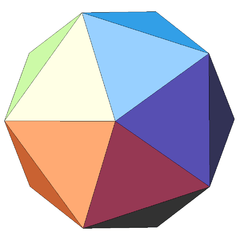
23	Compound of five octahedra (First compound stellation of icosahedron)	Ih
24	Compound of five tetrahedra (Second compound stellation of icosahedron)	I
25	Compound of ten tetrahedra (Third compound stellation of icosahedron)	Ih
26	Small triambic icosahedron (First stellation of icosahedron) (Triakis icosahedron)	Ih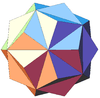
27	Second stellation of icosahedron	Ih
28	Excavated dodecahedron (Third stellation of icosahedron)	Ih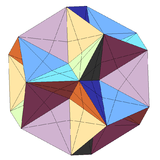
29	Fourth stellation of icosahedron	Ih
30	Fifth stellation of icosahedron	Ih
31	Sixth stellation of icosahedron	Ih
32	Seventh stellation of icosahedron	Ih
33	Eighth stellation of icosahedron	Ih
34	Ninth stellation of icosahedron Great triambic icosahedron	Ih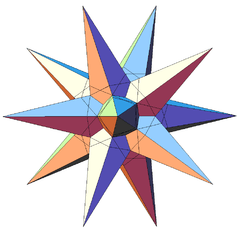
35	Tenth stellation of icosahedron	I
36	Eleventh stellation of icosahedron	I
37	Twelfth stellation of icosahedron	Ih
38	Thirteenth stellation of icosahedron	I
39	Fourteenth stellation of icosahedron	I
40	Fifteenth stellation of icosahedron	I
41	Great icosahedron (regular) (Sixteenth stellation of icosahedron)	Ih
42	Final stellation of the icosahedron	Ih

Stellations of cuboctahedron

Index	Name	Symmetry group	Picture	Facets (octahedral planes)	Facets (cube planes)
11	Cuboctahedron (regular)	Oh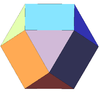
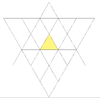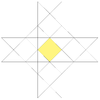43	Compound of cube and octahedron (First stellation of cuboctahedron)	Oh
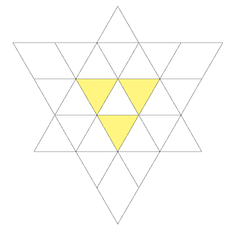44	Second stellation of cuboctahedron	Oh
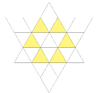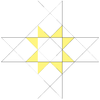45	Third stellation of cuboctahedron	Oh
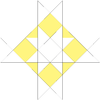46	Fourth stellation of cuboctahedron	Oh

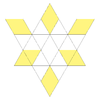Stellations of icosidodecahedron

Index	Name	Symmetry group	Picture	Facets (icosahedral planes)	Facets (dodecahedral planes)
12	Icosidodecahedron (regular)	Ih
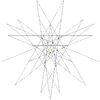47	(First stellation of icosidodecahedron) Compound of dodecahedron and icosahedron	Ih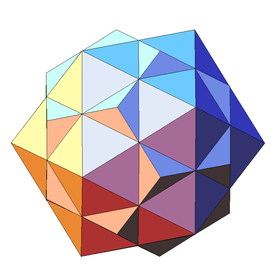
48	Second stellation of icosidodecahedron	Ih
49	Third stellation of icosidodecahedron	Ih
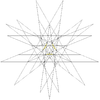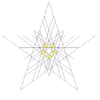50	Fourth stellation of icosidodecahedron (Compound of small stellated dodecahedron and triakis icosahedron)	Ih
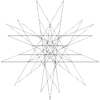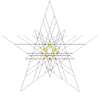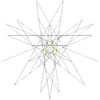
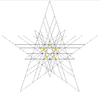
51	Fifth stellation of icosidodecahedron (Compound of small stellated dodecahedron and five octahedra)	Ih
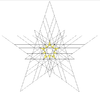
52	Sixth stellation of icosidodecahedron	Ih
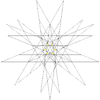53	Seventh stellation of icosidodecahedron	Ih
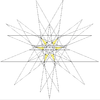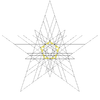54	Eighth stellation of icosidodecahedron (Compound of five tetrahedra and great dodecahedron)	I
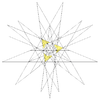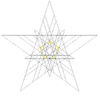55	Ninth stellation of icosidodecahedron	Ih
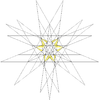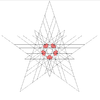56	Tenth stellation of icosidodecahedron	Ih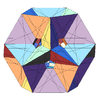
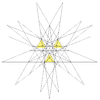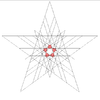57	Eleventh stellation of icosidodecahedron	Ih
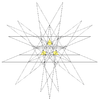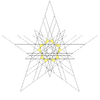58	Twelfth stellation of icosidodecahedron	Ih
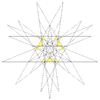59	Thirteenth stellation of icosidodecahedron	Ih
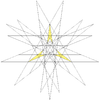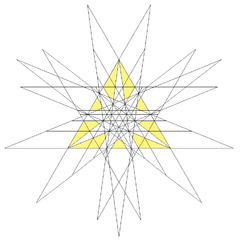
60	Fourteenth stellation of icosidodecahedron	Ih
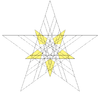
61	Compound of great stellated dodecahedron and great icosahedron	Ih
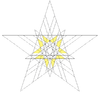
62	Fifteenth stellation of icosidodecahedron	Ih
63	Sixteenth stellation of icosidodecahedron	Ih
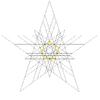64	Seventeenth stellation of icosidodecahedron	Ih
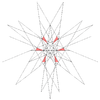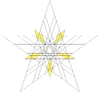65	Eighteenth stellation of icosidodecahedron	Ih
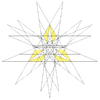66	Nineteenth stellation of icosidodecahedron	Ih

Uniform nonconvex solids W67 to W119

Index	Name	Picture	Dual name	Dual picture	Wythoff symbol	Vertex figure	Symmetry group	U#	K#	V	E	F	Faces by type
67	Tetrahemihexahedron		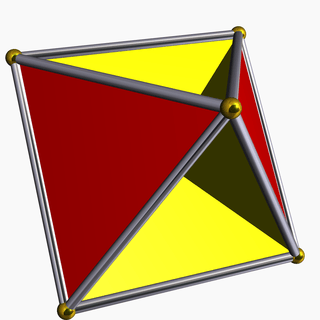Tetrahemihexacron		^3/23|2	4.^3/2.4.3	Td	U04	K09	6	12	7	4{3}+3{4}
68	Octahemioctahedron		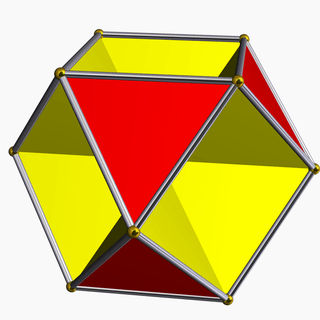Octahemioctacron		^3/23|3	6.^3/2.6.3	Oh	U03	K08	12	24	12	8{3}+4{6}
69	Small cubicuboctahedron		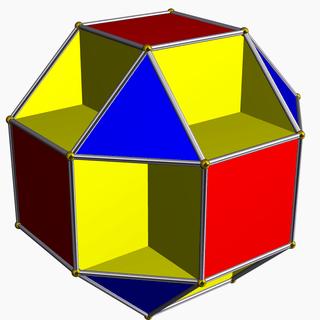Small hexacronic icositetrahedron		^3/24|4	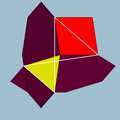8.^3/2.8.4	Oh	U13	K18	24	48	20	8{3}+6{4}+6{8}
70	Small ditrigonal icosidodecahedron		Small triambic icosahedron		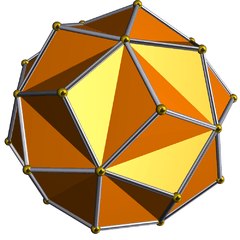3|^5/23	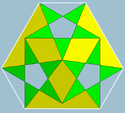(^5/2.3)^3	Ih	U30	K35	20	60	32	20{3}+12{^5/2}
71	Small icosicosidodecahedron		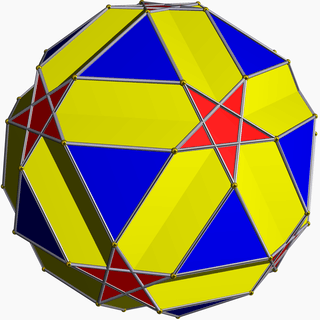Small icosacronic hexecontahedron		^5/23|3	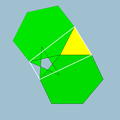6.^5/2.6.3	Ih	U31	K36	60	120	52	20{3}+12{^5/2}+20{6}
72	Small dodecicosidodecahedron		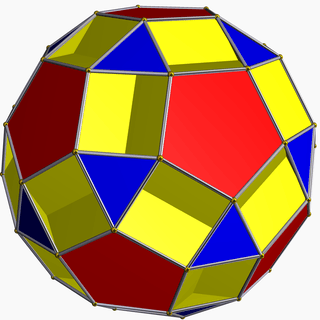Small dodecacronic hexecontahedron		^3/25|5	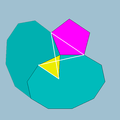10.^3/2.10.5	Ih	U33	K38	60	120	44	20{3}+12{5}+12{10}
73	Dodecadodecahedron		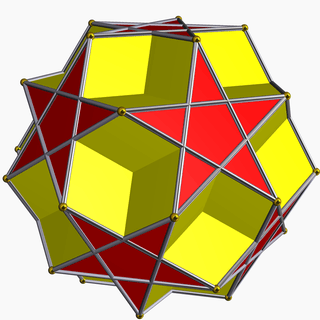Medial rhombic triacontahedron		2|^5/25	(^5/2.5)^2	Ih	U36	K41	30	60	24	12{5}+12{^5/2}
74	Small rhombidodecahedron		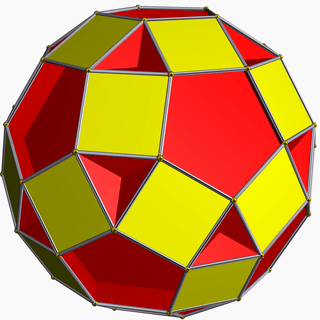Small rhombidodecacron		2^5/25|	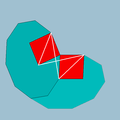10.4.^10/9.^4/3	Ih	U39	K44	60	120	42	30{4}+12{10}
75	Truncated great dodecahedron		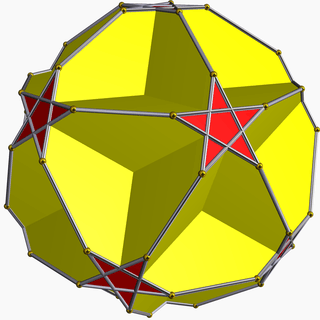Small stellapentakis dodecahedron		2^5/2|5	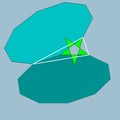10.10.^5/2	Ih	U37	K42	60	90	24	12{^5/2}+12{10}
76	Rhombidodecadodecahedron		Medial deltoidal hexecontahedron		^5/25|2	4.^5/2.4.5	Ih	U38	K43	60	120	54	30{4}+12{5}+12{^5/2}
77	Great cubicuboctahedron		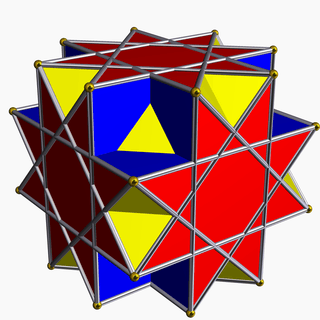Great hexacronic icositetrahedron		3 4|^4/3	^8/3.3.^8/3.4	Oh	U14	K19	24	48	20	8{3}+6{4}+6{^8/3}
78	Cubohemioctahedron		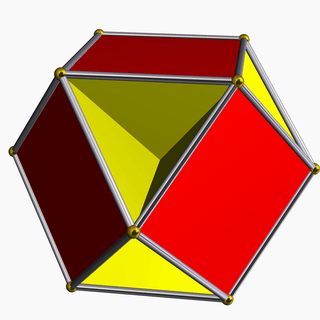Hexahemioctacron		^4/34|3	6.^4/3.6.4	Oh	U15	K20	12	24	10	6{4}+4{6}
79	Cubitruncated cuboctahedron (Cuboctatruncated cuboctahedron)		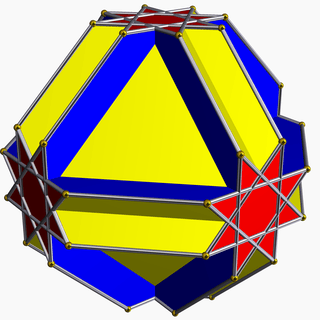Tetradyakis hexahedron		^4/33 4|	^8/3.6.8	Oh	U16	K21	48	72	20	8{6}+6{8}+6{^8/3}
80	Ditrigonal dodecadodecahedron		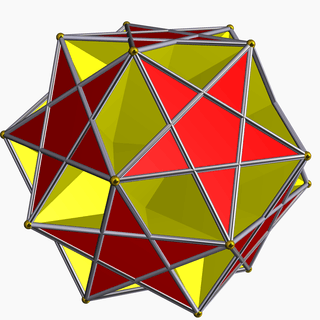Medial triambic icosahedron		3|^5/35	(^5/3.5)^3	Ih	U41	K46	20	60	24	12{5}+12{^5/2}
81	Great ditrigonal dodecicosidodecahedron		Great ditrigonal dodecacronic hexecontahedron		3 5|^5/3	^10/3.3.^10/3.5	Ih	U42	K47	60	120	44	20{3}+12{5}+12{^10/3}
82	Small ditrigonal dodecicosidodecahedron		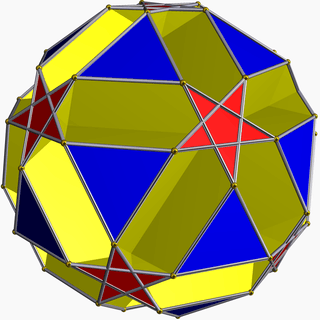Small ditrigonal dodecacronic hexecontahedron		^5/33|5	10.^5/3.10.3	Ih	U43	K48	60	120	44	20{3}+12{^5/2}+12{10}
83	Icosidodecadodecahedron		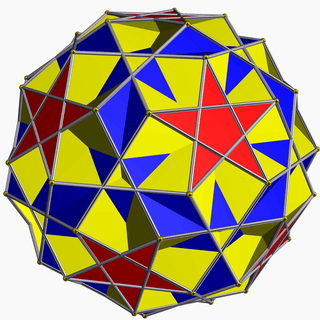Medial icosacronic hexecontahedron		^5/35|3	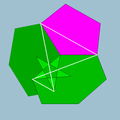6.^5/3.6.5	Ih	U44	K49	60	120	44	12{5}+12{^5/2}+20{6}
84	Icositruncated dodecadodecahedron (Icosidodecatruncated icosidodecahedron)		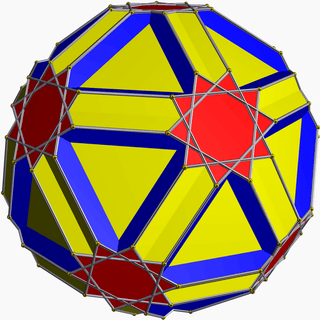Tridyakis icosahedron		^5/33 5|	^10/3.6.10	Ih	U45	K50	120	180	44	20{6}+12{10}+12{^10/3}
85	Nonconvex great rhombicuboctahedron (Quasirhombicuboctahedron)		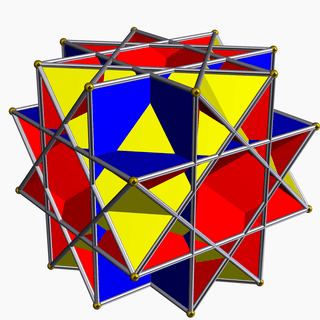Great deltoidal icositetrahedron		^3/24|2	4.^3/2.4.4	Oh	U17	K22	24	48	26	8{3}+(6+12){4}
86	Small rhombihexahedron		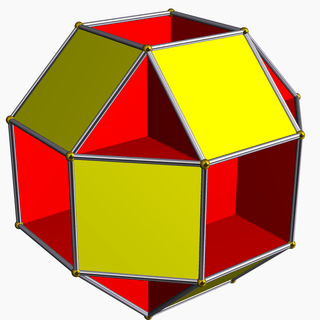Small rhombihexacron		^3/22 4|	4.8.^4/3.8	Oh	U18	K23	24	48	18	12{4}+6{8}
87	Great ditrigonal icosidodecahedron		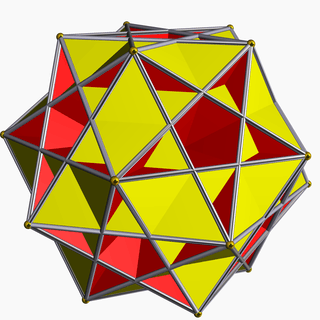Great triambic icosahedron		^3/2|3 5	(5.3.5.3.5.3)/2	Ih	U47	K52	20	60	32	20{3}+12{5}
88	Great icosicosidodecahedron		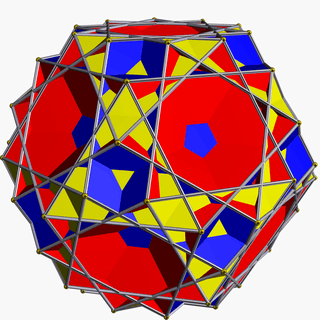Great icosacronic hexecontahedron		^3/25|3	6.^3/2.6.5	Ih	U48	K53	60	120	52	20{3}+12{5}+20{6}
89	Small icosihemidodecahedron		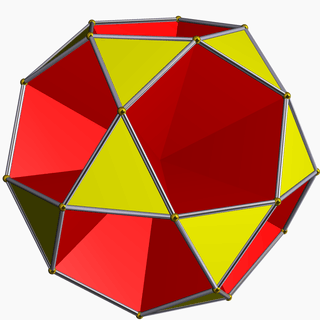Small icosihemidodecacron		^3/23|5	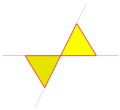10.^3/2.10.3	Ih	U49	K54	30	60	26	20{3}+6{10}
90	Small dodecicosahedron		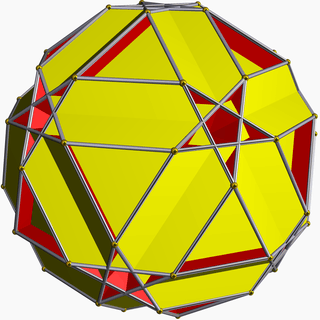Small dodecicosacron		^3/23 5|	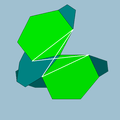10.6.^10/9.^6/5	Ih	U50	K55	60	120	32	20{6}+12{10}
91	Small dodecahemidodecahedron		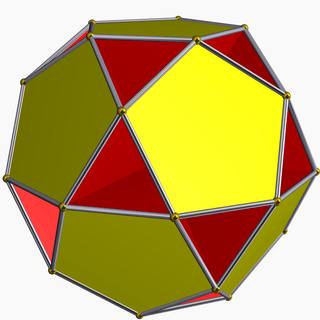Small dodecahemidodecacron		^5/45|5	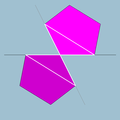10.^5/4.10.5	Ih	U51	K56	30	60	18	12{5}+6{10}
92	Stellated truncated hexahedron (Quasitruncated hexahedron)		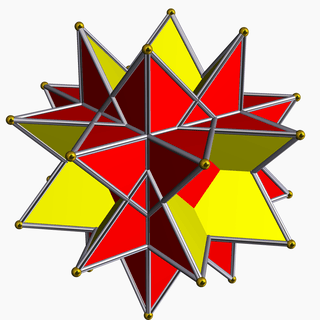Great triakis octahedron		2 3|^4/3	^8/3.^8/3.3	Oh	U19	K24	24	36	14	8{3}+6{^8/3}
93	Great truncated cuboctahedron (Quasitruncated cuboctahedron)		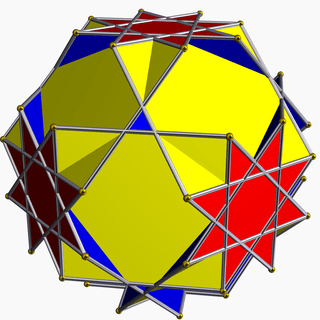Great disdyakis dodecahedron		^4/32 3|	^8/3.4.6	Oh	U20	K25	48	72	26	12{4}+8{6}+6{^8/3}
94	Great icosidodecahedron		Great rhombic triacontahedron		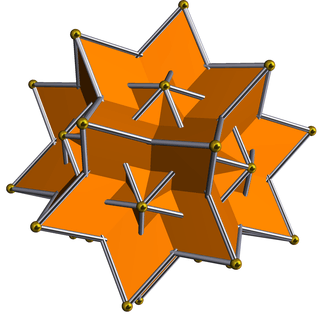2|^5/23	(^5/2.3)^2	Ih	U54	K59	30	60	32	20{3}+12{^5/2}
95	Truncated great icosahedron		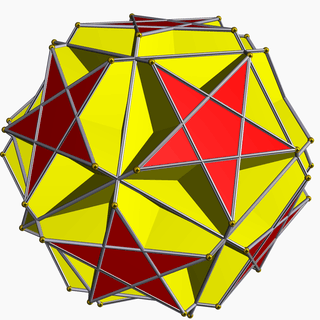Great stellapentakis dodecahedron		2^5/2|3	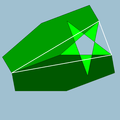6.6.^5/2	Ih	U55	K60	60	90	32	12{^5/2}+20{6}
96	Rhombicosahedron		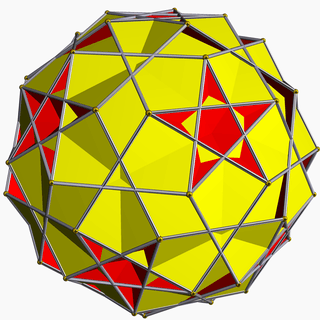Rhombicosacron		2^5/23|	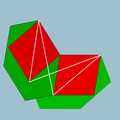6.4.^6/5.^4/3	Ih	U56	K61	60	120	50	30{4}+20{6}
97	Small stellated truncated dodecahedron (Quasitruncated small stellated dodecahedron)		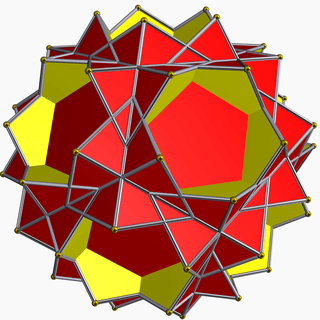Great pentakis dodecahedron		2 5|^5/3	^10/3.^10/3.5	Ih	U58	K63	60	90	24	12{5}+12{^10/3}
98	Truncated dodecadodecahedron (Quasitruncated dodecahedron)		Medial disdyakis triacontahedron		^5/32 5|	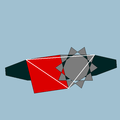^10/3.4.10	Ih	U59	K64	120	180	54	30{4}+12{10}+12{^10/3}
99	Great dodecicosidodecahedron		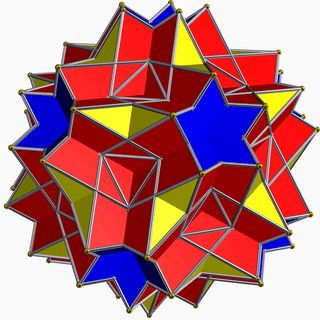Great dodecacronic hexecontahedron		^5/23|^5/3	^10/3.^5/2.^10/3.3	Ih	U61	K66	60	120	44	20{3}+12{^5/2}+12{^10/3}
100	Small dodecahemicosahedron		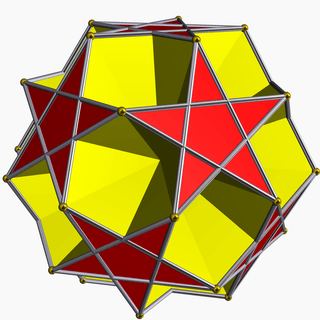Small dodecahemicosacron		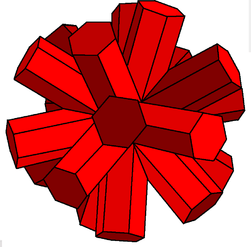^5/3^5/2|3	6.^5/3.6.^5/2	Ih	U62	K67	30	60	22	12{^5/2}+10{6}
101	Great dodecicosahedron		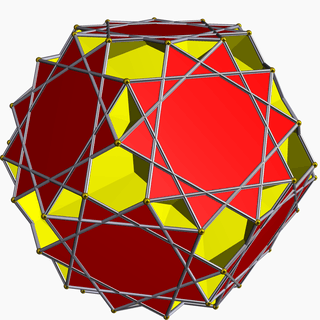Great dodecicosacron		^5/3^5/23|	6.^10/3.^6/5.^10/7	Ih	U63	K68	60	120	32	20{6}+12{^10/3}
102	Great dodecahemicosahedron		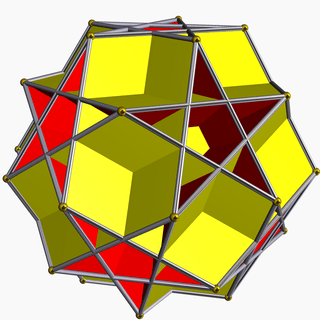Great dodecahemicosacron		^5/45|3	6.^5/4.6.5	Ih	U65	K70	30	60	22	12{5}+10{6}
103	Great rhombihexahedron		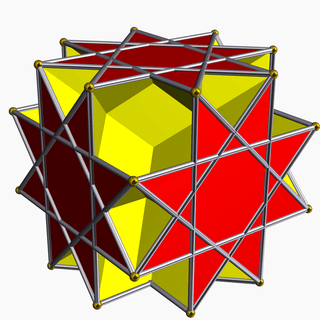Great rhombihexacron		^4/3^3/22|	4.^8/3.^4/3.^8/5	Oh	U21	K26	24	48	18	12{4}+6{^8/3}
104	Great stellated truncated dodecahedron (Quasitruncated great stellated dodecahedron)		Great triakis icosahedron		2 3|^5/3	^10/3.^10/3.3	Ih	U66	K71	60	90	32	20{3}+12{^10/3}
105	Nonconvex great rhombicosidodecahedron (Quasirhombicosidodecahedron)		Great deltoidal hexecontahedron		^5/33|2	4.^5/3.4.3	Ih	U67	K72	60	120	62	20{3}+30{4}+12{^5/2}
106	Great icosihemidodecahedron		Great icosihemidodecacron		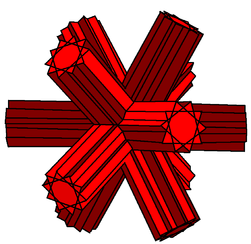3 3|^5/3	^10/3.^3/2.^10/3.3	Ih	U71	K76	30	60	26	20{3}+6{^10/3}
107	Great dodecahemidodecahedron		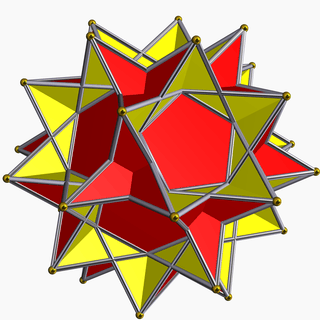Great dodecahemidodecacron		^5/3^5/2|^5/3	^10/3.^5/3.^10/3.^5/2	Ih	U70	K75	30	60	18	12{^5/2}+6{^10/3}
108	Great truncated icosidodecahedron (Great quasitruncated icosidodecahedron)		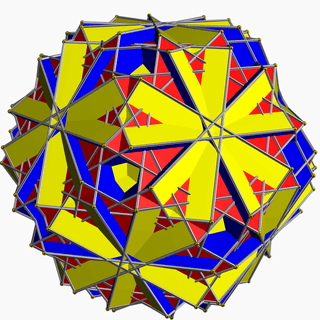Great disdyakis triacontahedron		^5/32 3|	^10/3.4.6	Ih	U68	K73	120	180	62	30{4}+20{6}+12{^10/3}
109	Great rhombidodecahedron		Great rhombidodecacron		^3/2^5/32|	4.^10/3.^4/3.^10/7	Ih	U73	K78	60	120	42	30{4}+12{^10/3}
110	Small snub icosicosidodecahedron		Small hexagonal hexecontahedron		|^5/23 3	3.3.3.3.3.^5/2	Ih	U32	K37	60	180	112	(40+60){3}+12{^5/2}
111	Snub dodecadodecahedron		Medial pentagonal hexecontahedron		|2^5/25	3.3.^5/2.3.5	I	U40	K45	60	150	84	60{3}+12{5}+12{^5/2}
112	Snub icosidodecadodecahedron		Medial hexagonal hexecontahedron		|^5/33 5	3.3.3.3.5.^5/3	I	U46	K51	60	180	104	(20+6){3}+12{5}+12{^5/2}
113	Great inverted snub icosidodecahedron		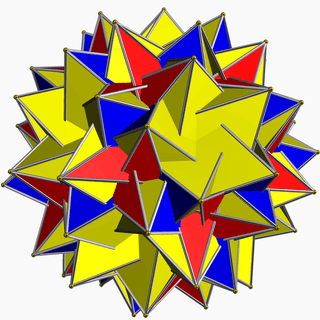Great inverted pentagonal hexecontahedron		|^5/32 3	3.3.3.3.^5/3	I	U69	K74	60	150	92	(20+60){3}+12{^5/2}
114	Inverted snub dodecadodecahedron		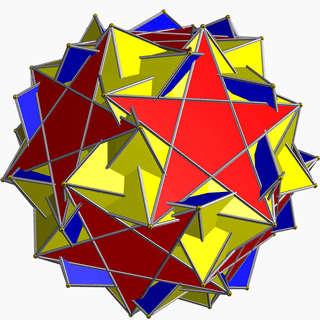Medial inverted pentagonal hexecontahedron		|^5/32 5	3.^5/3.3.3.5	I	U60	K65	60	150	84	60{3}+12{5}+12{^5/2}
115	Great snub dodecicosidodecahedron		Great hexagonal hexecontahedron		|^5/3^5/23	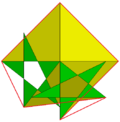3.^5/3.3.^5/2.3.3	I	U64	K69	60	180	104	(20+60){3}+(12+12){^5/2}
116	Great snub icosidodecahedron		Great pentagonal hexecontahedron		|2^5/2^5/2	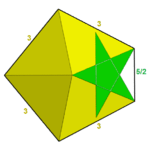3.3.3.3.^5/2	I	U57	K62	60	150	92	(20+60){3}+12{^5/2}
117	Great retrosnub icosidodecahedron		Great pentagrammic hexecontahedron		|^3/2^5/32	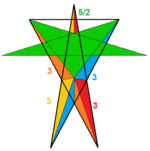(3.3.3.3.^5/2)/2	I	U74	K79	60	150	92	(20+60){3}+12{^5/2}
118	Small retrosnub icosicosidodecahedron		Small hexagrammic hexecontahedron		|^3/2^3/2^5/2	(3.3.3.3.3.^5/2)/2	Ih	U72	K77	180	60	112	(40+60){3}+12{^5/2}
119	Great dirhombicosidodecahedron		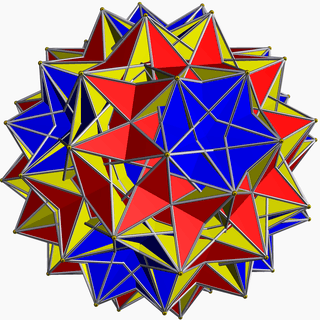Great dirhombicosidodecacron		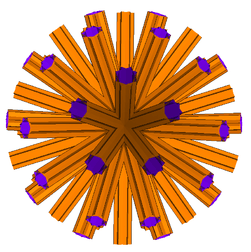|^3/2^5/33^5/2	(4.^5/3.4.3.4.^5/2.4.^3/2)/2	Ih	U75	K80	60	240	124	40{3}+60{4}+24{^5/2}

back to top

See also

• List of uniform polyhedra
• The fifty nine icosahedra
• List of polyhedral stellations

References

• Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
  • Errata
    • In Wenninger, the vertex figure for W90 is incorrectly shown as having parallel edges.
• Wenninger, Magnus (1979). Spherical Models. Cambridge University Press. ISBN 0-521-29432-0.

External links

• Magnus J. Wenninger
• Software used to generate images in this article:
  • Stella: Polyhedron Navigator Stella (software) - Can create and print nets for all of Wenninger's polyhedron models.
  • Vladimir Bulatov's Polyhedra Stellations Applet
  • Vladimir Bulatov's Polyhedra Stellations Applet packaged as an OS X application
• M. Wenninger, Polyhedron Models, Errata: known errors in the various editions.