Great truncated icosidodecahedron

In geometry, the great truncated icosidodecahedron (or great quasitruncated icosidodecahedron or stellatruncated icosidodecahedron) is a nonconvex uniform polyhedron, indexed as U₆₈. It has 62 faces (30 squares, 20 hexagons, and 12 decagrams), 180 edges, and 120 vertices.[1] It is given a Schläfli symbol t_0,1,2{​⁵⁄₃,3}, and Coxeter-Dynkin diagram, .

Great truncated icosidodecahedron
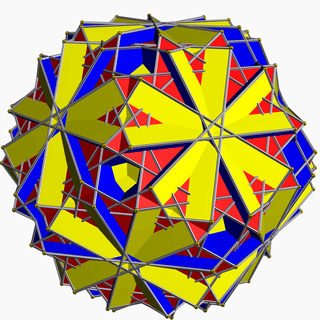Type	Uniform star polyhedron
Elements	F = 62, E = 180 V = 120 (χ = 2)
Faces by sides	30{4}+20{6}+12{10/3}
Wythoff symbol	2 3 5/3 |
Symmetry group	Ih, [5,3], *532
Index references	U68, C87, W108
Dual polyhedron	Great disdyakis triacontahedron
Vertex figure	4.6.10/3
Bowers acronym	Gaquatid

3D model of a great truncated icosidodecahedron

Cartesian coordinates

Cartesian coordinates for the vertices of a great truncated icosidodecahedron centered at the origin are all the even permutations of

(±τ, ±τ, ±(3−1/τ)),

(±2τ, ±1/τ, ±τ⁻³),

(±τ, ±1/τ², ±(1+3/τ)),

(±√5, ±2, ±√5/τ) and

(±1/τ, ±3, ±2/τ),

where τ = (1+√5)/2 is the golden ratio.

Related polyhedra

Great disdyakis triacontahedron

Great disdyakis triacontahedron
Type	Star polyhedron
Face
Elements	F = 120, E = 180 V = 62 (χ = 2)
Symmetry group	Ih, [5,3], *532
Index references	DU68
dual polyhedron	Great truncated icosidodecahedron

3D model of a great disdyakis triacontahedron

The great disdyakis triacontahedron (or trisdyakis icosahedron) is a nonconvex isohedral polyhedron. It is the dual of the great truncated icosidodecahedron. Its faces are triangles.

Proportions

The triangles have one angle of ${\displaystyle \arccos({\frac {1}{6}}+{\frac {1}{15}}{\sqrt {5}})\approx 71.594\,636\,220\,88^{\circ }}$, one of ${\displaystyle \arccos({\frac {3}{4}}+{\frac {1}{10}}{\sqrt {5}})\approx 13.192\,999\,040\,74^{\circ }}$ and one of ${\displaystyle \arccos({\frac {3}{8}}-{\frac {5}{24}}{\sqrt {5}})\approx 95.212\,364\,738\,38^{\circ }}$. The dihedral angle equals ${\displaystyle \arccos({\frac {-179+24{\sqrt {5}}}{241}})\approx 121.336\,250\,807\,39^{\circ }}$. Part of each triangle lies within the solid, hence is invisible in solid models.

See also

• List of uniform polyhedra

References

1. Maeder, Roman. "68: great truncated icosidodecahedron". MathConsult.

• Wenninger, Magnus (1983), Dual Models, Cambridge University Press, doi:10.1017/CBO9780511569371, ISBN 978-0-521-54325-5, MR 0730208 p. 96

External links

• Weisstein, Eric W. "Great truncated icosidodecahedron". MathWorld.
• Weisstein, Eric W. "Great disdyakis triacontahedron". MathWorld.