Compound of five octahedra
The compound of five octahedra is one of the five regular polyhedron compounds. This polyhedron can be seen as either a polyhedral stellation or a compound. This compound was first described by Edmund Hess in 1876. It is unique among the regular compounds for not having a regular convex hull.
| Compound of five octahedra | |
|---|---|
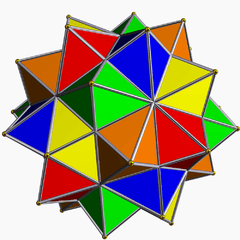 | |
| Type | Regular compound |
| Index | UC17, W23 |
| Coxeter symbol | [5{3,4}]2{3,5}[1] |
| Elements (As a compound) | 5 octahedra: F = 40, E = 60, V = 30 |
| Dual compound | Compound of five cubes |
| Symmetry group | icosahedral (Ih) |
| Subgroup restricting to one constituent | pyritohedral (Th) |
.stl.png)
As a stellation
It is the second stellation of the icosahedron, and given as Wenninger model index 23.
It can be constructed by a rhombic triacontahedron with rhombic-based pyramids added to all the faces, as shown by the five colored model image. (This construction does not generate the regular compound of five octahedra, but shares the same topology and can be smoothly deformed into the regular compound.)
It has a density of greater than 1.
| Stellation diagram | Stellation core | Convex hull |
|---|---|---|
 |
 Icosahedron |
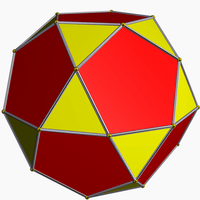 Icosidodecahedron |
As a compound
It can also be seen as a polyhedral compound of five octahedra arranged in icosahedral symmetry (Ih).
It shares its edges and half of its triangular faces with the compound of five tetrahemihexahedra.
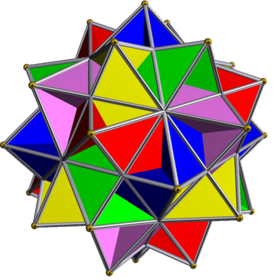 Compound of five tetrahemihexahedra |
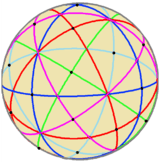 As a spherical tiling the octahedra edges match the disdyakis triacontahedron |
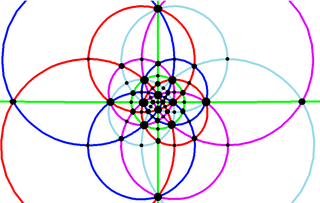 Stereographic projection |
As a faceting
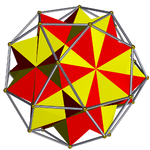
It is also a faceting of an icosidodecahedron, shown at left.
Other 5-octahedra compounds
A second 5-octahedra compound, with octahedral symmetry, also exists. It can be generated by adding a fifth octahedra to the standard 4-octahedra compound.
See also
References
- Regular polytopes, pp.49-50, p.98
- Peter R. Cromwell, Polyhedra, Cambridge, 1997.
- Wenninger, Magnus (1974). Polyhedron Models. Cambridge University Press. ISBN 0-521-09859-9.
- Coxeter, Harold Scott MacDonald; Du Val, P.; Flather, H. T.; Petrie, J. F. (1999). The fifty-nine icosahedra (3rd ed.). Tarquin. ISBN 978-1-899618-32-3. MR 0676126. (1st Edn University of Toronto (1938))
- H.S.M. Coxeter, Regular Polytopes, (3rd edition, 1973), Dover edition, ISBN 0-486-61480-8, 3.6 The five regular compounds, pp.47-50, 6.2 Stellating the Platonic solids, pp.96-104
- E. Hess 1876 Zugleich Gleicheckigen und Gleichflächigen Polyeder, Schriften der Gesellschaft zur Berörderung der Gasammten Naturwissenschaften zu Marburg 11 (1876) pp 5–97.
External links
- MathWorld: Octahedron5-Compound
- Paper Model Compound of Five Octahedra
- VRML model:
- Klitzing, Richard. "3D compound".
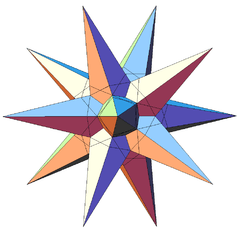
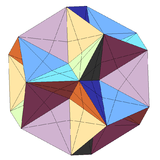
| Notable stellations of the icosahedron | |||||||||
| Regular | Uniform duals | Regular compounds | Regular star | Others | |||||
| (Convex) icosahedron | Small triambic icosahedron | Medial triambic icosahedron | Great triambic icosahedron | Compound of five octahedra | Compound of five tetrahedra | Compound of ten tetrahedra | Great icosahedron | Excavated dodecahedron | Final stellation |
|---|---|---|---|---|---|---|---|---|---|
 |
 |
 |
 |
 |
 |
 |
 |
 | |
 |
 |
 |
 |
 |
 |
 |
 |
 | |
| The stellation process on the icosahedron creates a number of related polyhedra and compounds with icosahedral symmetry. | |||||||||