Ditrigonal dodecadodecahedron
In geometry, the ditrigonal dodecadodecahedron (or ditrigonary dodecadodecahedron) is a nonconvex uniform polyhedron, indexed as U41. It has 24 faces (12 pentagons and 12 pentagrams), 60 edges, and 20 vertices.[1] It has extended Schläfli symbol b{5,5⁄2}, as a blended great dodecahedron, and Coxeter diagram ![]()
![]()
![]()
![]()
![]()
![]()
| Ditrigonal dodecadodecahedron | |
|---|---|
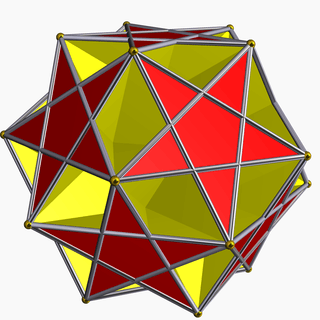 | |
| Type | Uniform star polyhedron |
| Elements | F = 24, E = 60 V = 20 (χ = −16) |
| Faces by sides | 12{5}+12{5/2} |
| Wythoff symbol | 3 | 5/3 5 3/2 | 5 5/2 3/2 | 5/3 5/4 3 | 5/2 5/4 |
| Symmetry group | Ih, [5,3], *532 |
| Index references | U41, C53, W80 |
| Dual polyhedron | Medial triambic icosahedron |
| Vertex figure |  (5.5/3)3 |
| Bowers acronym | Ditdid |

Related polyhedra
Its convex hull is a regular dodecahedron. It additionally shares its edge arrangement with the small ditrigonal icosidodecahedron (having the pentagrammic faces in common), the great ditrigonal icosidodecahedron (having the pentagonal faces in common), and the regular compound of five cubes.
| a{5,3} | a{5⁄2,3} | b{5,5⁄2} |
|---|---|---|
 Small ditrigonal icosidodecahedron |
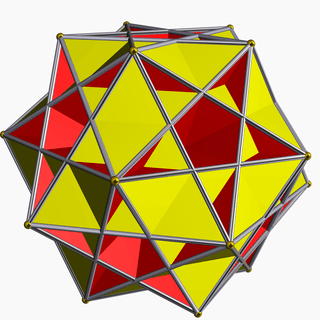 Great ditrigonal icosidodecahedron |
 Ditrigonal dodecadodecahedron |
 Dodecahedron (convex hull) |
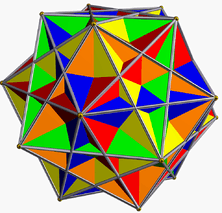 Compound of five cubes |
Furthermore, it may be viewed as a facetted dodecahedron: the pentagonal faces may be inscribed within the dodecahedron's pentagons. Its dual, the medial triambic icosahedron, is a stellation of the icosahedron.
It is topologically equivalent to a quotient space of the hyperbolic order-6 pentagonal tiling, by distorting the pentagrams back into regular pentagons. As such, it is a regular polyhedron of index two:[2]

See also
References
- Maeder, Roman. "41: ditrigonal dodecadodecahedron". MathConsult.
- The Regular Polyhedra (of index two), David A. Richter