Prismatic uniform 4-polytope

In four-dimensional geometry, a prismatic uniform 4-polytope is a uniform 4-polytope with a nonconnected Coxeter diagram symmetry group. These figures are analogous to the set of prisms and antiprism uniform polyhedra, but add a third category called duoprisms, constructed as a product of two regular polygons.

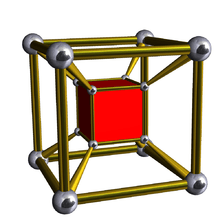
A cubic prism, {4,3}×{}, is a lower symmetry construction of the regular tesseract, {4,3,3}, as a prism of two parallel cubes, as seen in this Schlegel diagram

The prismatic uniform 4-polytopes consist of two infinite families:

  • Polyhedral prisms: products of a line segment and a uniform polyhedron. This family is infinite because it includes prisms built on 3-dimensional prisms and antiprisms.
  • Duoprisms: product of two regular polygons.

Convex polyhedral prisms

The most obvious family of prismatic 4-polytopes is the polyhedral prisms, i.e. products of a polyhedron with a line segment. The cells of such a 4-polytope are two identical uniform polyhedra lying in parallel hyperplanes (the base cells) and a layer of prisms joining them (the lateral cells). This family includes prisms for the 75 nonprismatic uniform polyhedra (of which 18 are convex; one of these, the cube-prism, is listed above as the tesseract).

There are 18 convex polyhedral prisms created from 5 Platonic solids and 13 Archimedean solids as well as for the infinite families of three-dimensional prisms and antiprisms. The symmetry number of a polyhedral prism is twice that of the base polyhedron.

Tetrahedral prisms: A3 × A1
# Johnson Name (Bowers style acronym) Picture Coxeter diagram
and Schläfli
symbols		 Cells by type Element counts
Cells Faces Edges Vertices
48 Tetrahedral prism (tepe)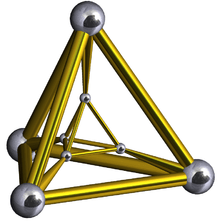
{3,3}×{}		 2
3.3.3		 4
3.4.4		 6 8 {3}
6 {4}		 16 8
49 Truncated tetrahedral prism (tuttip)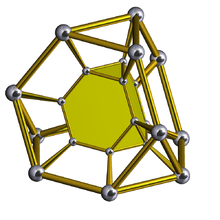
t{3,3}×{}		 2
3.6.6		 4
3.4.4		 4
4.4.6		 10 8 {3}
18 {4}
8 {6}		 48 24
[51] Rectified tetrahedral prism
(Same as octahedral prism) (ope)
r{3,3}×{}		 2
3.3.3.3		 4
3.4.4		 6 16 {3}
12 {4}		 30 12
[50] Cantellated tetrahedral prism
(Same as cuboctahedral prism) (cope)
rr{3,3}×{}		 2
3.4.3.4		 8
3.4.4		 6
4.4.4		 16 16 {3}
36 {4}		 60 24
[54] Cantitruncated tetrahedral prism
(Same as truncated octahedral prism) (tope)
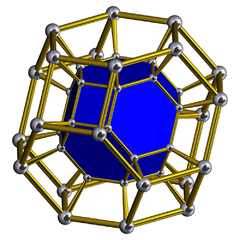tr{3,3}×{}		 2
4.6.6		 8
3.4.4		 6
4.4.4		 16 48 {4}
16 {6}		 96 48
[59] Snub tetrahedral prism
(Same as icosahedral prism) (ipe)
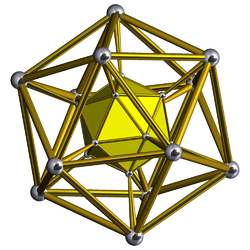sr{3,3}×{}		 2
3.3.3.3.3		 20
3.4.4		 22 40 {3}
30 {4}		 72 24

Octahedral prisms: BC3 × A1
# Johnson Name (Bowers style acronym) Picture Coxeter diagram
and Schläfli
symbols		 Cells by type Element counts
Cells Faces Edges Vertices
[10] Cubic prism
(Same as tesseract)
(Same as 4-4 duoprism) (tes)
{4,3}×{}		 2
4.4.4		 6
4.4.4		 8 24 {4} 32 16
50 Cuboctahedral prism
(Same as cantellated tetrahedral prism) (cope)
r{4,3}×{}		 2
3.4.3.4		 8
3.4.4		 6
4.4.4		 16 16 {3}
36 {4}		 60 24
51 Octahedral prism
(Same as rectified tetrahedral prism)
(Same as triangular antiprismatic prism) (ope)
{3,4}×{}		 2
3.3.3.3		 8
3.4.4		 10 16 {3}
12 {4}		 30 12
52 Rhombicuboctahedral prism (sircope)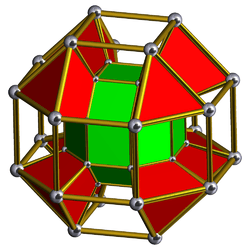
rr{4,3}×{}		 2
3.4.4.4		 8
3.4.4		 18
4.4.4		 28 16 {3}
84 {4}		 120 96
53 Truncated cubic prism (ticcup)
t{4,3}×{}		 2
3.8.8		 8
3.4.4		 6
4.4.8		 16 16 {3}
36 {4}
12 {8}		 96 48
54 Truncated octahedral prism
(Same as cantitruncated tetrahedral prism) (tope)
t{3,4}×{}		 2
4.6.6		 6
4.4.4		 8
4.4.6		 16 48 {4}
16 {6}		 96 48
55 Truncated cuboctahedral prism (gircope)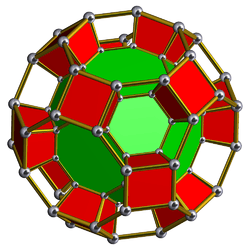
tr{4,3}×{}		 2
4.6.8		 12
4.4.4		 8
4.4.6		 6
4.4.8		 28 96 {4}
16 {6}
12 {8}		 192 96
56 Snub cubic prism (sniccup)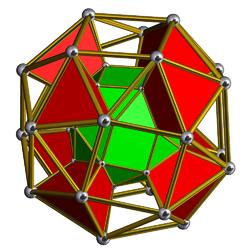
sr{4,3}×{}		 2
3.3.3.3.4		 32
3.4.4		 6
4.4.4		 40 64 {3}
72 {4}		 144 48

Icosahedral prisms: H3 × A1
# Johnson Name (Bowers style acronym) Picture Coxeter diagram
and Schläfli
symbols		 Cells by type Element counts
Cells Faces Edges Vertices
57 Dodecahedral prism (dope)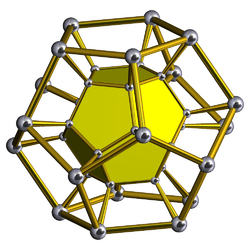
{5,3}×{}		 2
5.5.5		 12
4.4.5		 14 30 {4}
24 {5}		 80 40
58 Icosidodecahedral prism (iddip)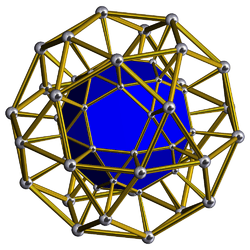
r{5,3}×{}		 2
3.5.3.5		 20
3.4.4		 12
4.4.5		 34 40 {3}
60 {4}
24 {5}		 150 60
59 Icosahedral prism
(same as snub tetrahedral prism) (ipe)
{3,5}×{}		 2
3.3.3.3.3		 20
3.4.4		 22 40 {3}
30 {4}		 72 24
60 Truncated dodecahedral prism (tiddip)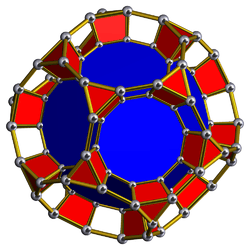
t{5,3}×{}		 2
3.10.10		 20
3.4.4		 12
4.4.5		 34 40 {3}
90 {4}
24 {10}		 240 120
61 Rhombicosidodecahedral prism (sriddip)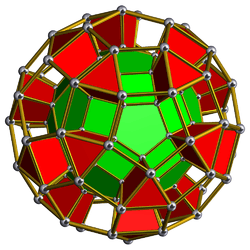
rr{5,3}×{}		 2
3.4.5.4		 20
3.4.4		 30
4.4.4		 12
4.4.5		 64 40 {3}
180 {4}
24 {5}		 300 120
62 Truncated icosahedral prism (tipe)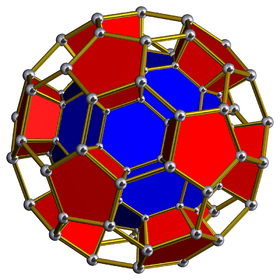
t{3,5}×{}		 2
5.6.6		 12
4.4.5		 20
4.4.6		 34 90 {4}
24 {5}
40 {6}		 240 120
63 Truncated icosidodecahedral prism (griddip)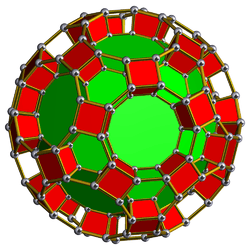
tr{5,3}×{}		 2
4.6.4.10		 30
4.4.4		 20
4.4.6		 12
4.4.10		 64 240 {4}
40 {6}
24 {5}		 480 240
64 Snub dodecahedral prism (sniddip)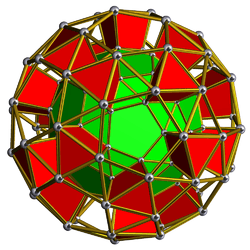
sr{5,3}×{}		 2
3.3.3.3.5		 80
3.4.4		 12
4.4.5		 94 240 {4}
40 {6}
24 {10}		 360 120

Duoprisms: [p] × [q]
Set of uniform p,q duoprisms

3-3
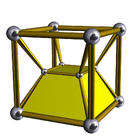3-4
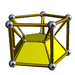3-5
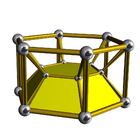3-6
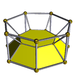3-7
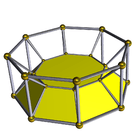3-8

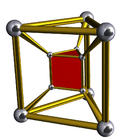4-3
4-4
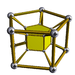4-5
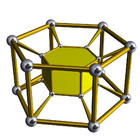4-6
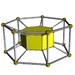4-7
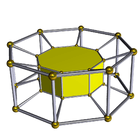4-8

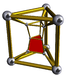5-3
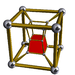5-4
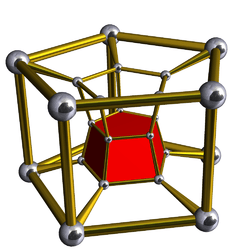5-5
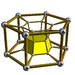5-6
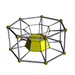5-7
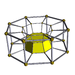5-8

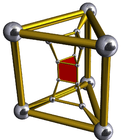6-3
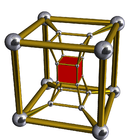6-4
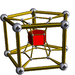6-5
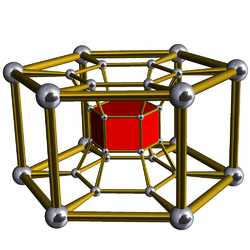6-6
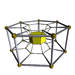6-7
6-8

7-3
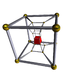7-4
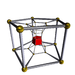7-5
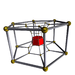7-6
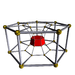7-7
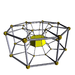7-8

8-3
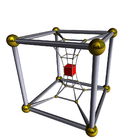8-4
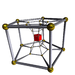8-5
8-6
8-7
8-8

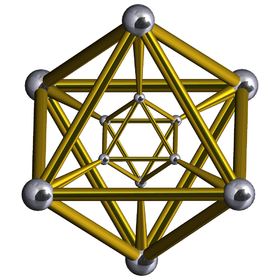
The second is the infinite family of uniform duoprisms, products of two regular polygons.

Their Coxeter diagram is of the form

This family overlaps with the first: when one of the two "factor" polygons is a square, the product is equivalent to a hyperprism whose base is a three-dimensional prism. The symmetry number of a duoprism whose factors are a p-gon and a q-gon (a "p,q-duoprism") is 4pq if p≠q; if the factors are both p-gons, the symmetry number is 8p2. The tesseract can also be considered a 4,4-duoprism.

The elements of a p,q-duoprism (p ≥ 3, q ≥ 3) are:

  • Cells: p q-gonal prisms, q p-gonal prisms
  • Faces: pq squares, p q-gons, q p-gons
  • Edges: 2pq
  • Vertices: pq

There is no uniform analogue in four dimensions to the infinite family of three-dimensional antiprisms with the exception of the great duoantiprism.

Infinite set of p-q duoprism - - p q-gonal prisms, q p-gonal prisms:

  • 3-3 duoprism - - 6 triangular prisms
  • 3-4 duoprism - - 3 cubes, 4 triangular prisms
  • 4-4 duoprism - - 8 cubes (same as tesseract)
  • 3-5 duoprism - - 3 pentagonal prisms, 5 triangular prisms
  • 4-5 duoprism - - 4 pentagonal prisms, 5 cubes
  • 5-5 duoprism - - 10 pentagonal prisms
  • 3-6 duoprism - - 3 hexagonal prisms, 6 triangular prisms
  • 4-6 duoprism - - 4 hexagonal prisms, 6 cubes
  • 5-6 duoprism - - 5 hexagonal prisms, 6 pentagonal prisms
  • 6-6 duoprism - - 12 hexagonal prisms
  • ...

Polygonal prismatic prisms

The infinite set of uniform prismatic prisms overlaps with the 4-p duoprisms: (p≥3) - - p cubes and 4 p-gonal prisms - (All are the same as 4-p duoprism)

  • Triangular prismatic prism - - 3 cubes and 4 triangular prisms - (same as 3-4 duoprism)
  • Square prismatic prism - - 4 cubes and 4 cubes - (same as 4-4 duoprism and same as tesseract)
  • Pentagonal prismatic prism - - 5 cubes and 4 pentagonal prisms - (same as 4-5 duoprism)
  • Hexagonal prismatic prism - - 6 cubes and 4 hexagonal prisms - (same as 4-6 duoprism)
  • Heptagonal prismatic prism - - 7 cubes and 4 heptagonal prisms - (same as 4-7 duoprism)
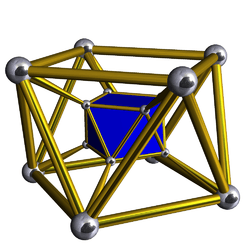
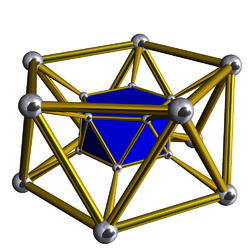
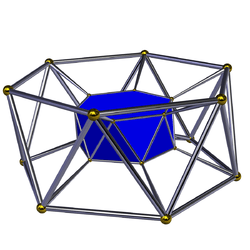
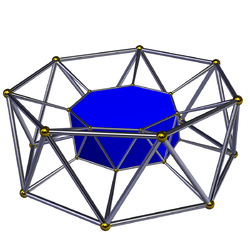
  • Octagonal prismatic prism - - 8 cubes and 4 octagonal prisms - (same as 4-8 duoprism)
  • ...

Uniform antiprismatic prism

The infinite sets of uniform antiprismatic prisms or antiduoprisms are constructed from two parallel uniform antiprisms: (p≥3) - - 2 p-gonal antiprisms, connected by 2 p-gonal prisms and 2p triangular prisms.

Convex p-gonal antiprismatic prisms
Name s{2,2}×{} s{2,3}×{} s{2,4}×{} s{2,5}×{} s{2,6}×{} s{2,7}×{} s{2,8}×{} s{2,p}×{}
Coxeter
diagram







Image
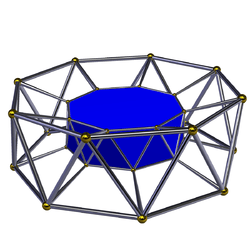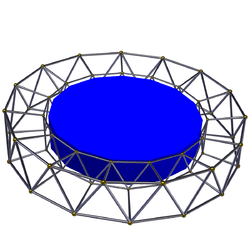Vertex
figure
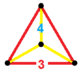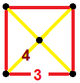Cells 2 s{2,2}
(2) {2}×{}={4}
4 {3}×{}		 2 s{2,3}
2 {3}×{}
6 {3}×{}		 2 s{2,4}
2 {4}×{}
8 {3}×{}		 2 s{2,5}
2 {5}×{}
10 {3}×{}		 2 s{2,6}
2 {6}×{}
12 {3}×{}		 2 s{2,7}
2 {7}×{}
14 {3}×{}		 2 s{2,8}
2 {8}×{}
16 {3}×{}		 2 s{2,p}
2 {p}×{}
2p {3}×{}
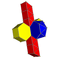
Net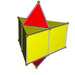

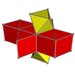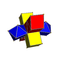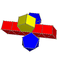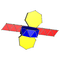
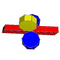
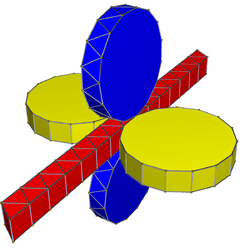A p-gonal antiprismatic prism has 4p triangle, 4p square and 4 p-gon faces. It has 10p edges, and 4p vertices.

gollark: Just summarize it.
gollark: This is acceptable.
gollark: I don't think it's *entirely* free, there are roughly consistent patterns.
gollark: ↑ revised marketing material
gollark: https://media.discordapp.net/attachments/461970193728667648/779802718075355166/unknown.png

References
  • Kaleidoscopes: Selected Writings of H.S.M. Coxeter, edited by F. Arthur Sherk, Peter McMullen, Anthony C. Thompson, Asia Ivic Weiss, Wiley-Interscience Publication, 1995, ISBN 978-0-471-01003-6
    • (Paper 22) H.S.M. Coxeter, Regular and Semi-Regular Polytopes I, [Math. Zeit. 46 (1940) 380-407, MR 2,10]
    • (Paper 23) H.S.M. Coxeter, Regular and Semi-Regular Polytopes II, [Math. Zeit. 188 (1985) 559-591]
    • (Paper 24) H.S.M. Coxeter, Regular and Semi-Regular Polytopes III, [Math. Zeit. 200 (1988) 3-45]
  • J.H. Conway and M.J.T. Guy: Four-Dimensional Archimedean Polytopes, Proceedings of the Colloquium on Convexity at Copenhagen, page 38 und 39, 1965
  • N.W. Johnson: The Theory of Uniform Polytopes and Honeycombs, Ph.D. Dissertation, University of Toronto, 1966
  • Four-dimensional Archimedean Polytopes (German), Marco Möller, 2004 PhD dissertation
  • Klitzing, Richard. "4D uniform polytopes (polychora)".
Fundamental convex regular and uniform polytopes in dimensions 2–10
Family An Bn I2(p) / Dn E6 / E7 / E8 / F4 / G2 Hn
Regular polygon Triangle Square p-gon Hexagon Pentagon
Uniform polyhedron Tetrahedron Octahedron • Cube Demicube Dodecahedron • Icosahedron
Uniform 4-polytope 5-cell 16-cell • Tesseract Demitesseract 24-cell 120-cell • 600-cell
Uniform 5-polytope 5-simplex 5-orthoplex • 5-cube 5-demicube
Uniform 6-polytope 6-simplex 6-orthoplex • 6-cube 6-demicube 122 • 221
Uniform 7-polytope 7-simplex 7-orthoplex • 7-cube 7-demicube 132 • 231 • 321
Uniform 8-polytope 8-simplex 8-orthoplex • 8-cube 8-demicube 142 • 241 • 421
Uniform 9-polytope 9-simplex 9-orthoplex • 9-cube 9-demicube
Uniform 10-polytope 10-simplex 10-orthoplex • 10-cube 10-demicube
Uniform n-polytope n-simplex n-orthoplex • n-cube n-demicube 1k2 • 2k1 • k21 n-pentagonal polytope
Topics: Polytope families • Regular polytope • List of regular polytopes and compounds
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.