Isotonic regression

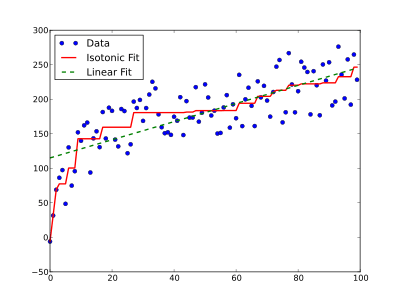
In statistics, isotonic regression or monotonic regression is the technique of fitting a free-form line to a sequence of observations such that the fitted line is non-decreasing (or non-increasing) everywhere, and lies as close to the observations as possible.

An example of isotonic regression (solid red line) compared to linear regression on the same data, both fit to minimize the mean squared error. The free-form property of isotonic regression means the line can be steeper where the data are steeper; the isotonicity constraint means the line does not decrease.

Applications

Isotonic regression has applications in statistical inference. For example, one might use it to fit an isotonic curve to the means of some set of experimental results when an increase in those means according to some particular ordering is expected. A benefit of isotonic regression is that it is not constrained by any functional form, such as the linearity imposed by linear regression, as long as the function is monotonic increasing.

Another application is nonmetric multidimensional scaling,[1] where a low-dimensional embedding for data points is sought such that order of distances between points in the embedding matches order of dissimilarity between points. Isotonic regression is used iteratively to fit ideal distances to preserve relative dissimilarity order.

Isotonic regression is also used in probablistic classification to calibrate the predicted probabilities of supervised machine learning models.[2]

Software for computing isotone (monotonic) regression has been developed for R,[3] Stata, and Python.[4]

Algorithms

In terms of numerical analysis, isotonic regression involves finding a weighted least-squares fit ${\displaystyle x\in \mathbb {R} ^{n}}$ to a vector ${\displaystyle a\in \mathbb {R} ^{n}}$ with weights vector ${\displaystyle w\in \mathbb {R} ^{n}}$ subject to a set of non-contradictory constraints of the kind ${\displaystyle x_{i}\leq x_{j}}$. The usual choice for the constraints is ${\displaystyle x_{i}\leq x_{i+1}}$, or in other words: every point must be at least as high as the previous point.

Such constraints define a partial ordering or total ordering and can be represented as a directed graph ${\displaystyle G=(N,E)}$, where ${\displaystyle N}$ (nodes) is the set of variables (observed values) involved, and ${\displaystyle E}$ (edges) is the set of pairs ${\displaystyle (i,j)}$ for each constraint ${\displaystyle x_{i}\leq x_{j}}$. Thus, the isotonic regression problem corresponds to the following quadratic program (QP):

${\displaystyle \min \sum _{i=1}^{n}w_{i}(x_{i}-a_{i})^{2}}$ ${\displaystyle {\text{subject to }}x_{i}\leq x_{j}{\text{ for all }}(i,j)\in E.}$

In the case when ${\displaystyle G=(N,E)}$ is a total ordering, a simple iterative algorithm for solving this quadratic program is called the pool adjacent violators algorithm. Conversely, Best and Chakravarti (1990) studied the problem as an active set identification problem, and proposed a primal algorithm. These two algorithms can be seen as each other's dual, and both have a computational complexity of ${\displaystyle O(n).}$[5]

Simply ordered case

To illustrate the above, let the ${\displaystyle x_{i}\leq x_{j}}$ constraints be ${\displaystyle x_{1}\leq x_{2}\leq \ldots \leq x_{n}}$.

The isotonic estimator, ${\displaystyle g^{*}}$, minimizes the weighted least squares-like condition:

${\displaystyle \min _{g\in {\mathcal {A}}}\sum _{i=1}^{n}w_{i}(g(x_{i})-f(x_{i}))^{2}}$

where ${\displaystyle {\mathcal {A}}}$ is the set of all piecewise linear, non-decreasing, continuous functions and ${\displaystyle f}$ is a known function.

References

1. Kruskal, J. B. (1964). "Nonmetric Multidimensional Scaling: A numerical method". Psychometrika. 29 (2): 115–129. doi:10.1007/BF02289694.
2. "Predicting good probabilities with supervised learning | Proceedings of the 22nd international conference on Machine learning". dl.acm.org. Retrieved 2020-07-07.
3. Leeuw, Jan de; Hornik, Kurt; Mair, Patrick (2009). "Isotone Optimization in R: Pool-Adjacent-Violators Algorithm (PAVA) and Active Set Methods". Journal of Statistical Software. 32 (5): 1–24. doi:10.18637/jss.v032.i05. ISSN 1548-7660.
4. Pedregosa, Fabian; et al. (2011). "Scikit-learn:Machine learning in Python". Journal of Machine Learning Research. 12: 2825–2830. arXiv:1201.0490. Bibcode:2012arXiv1201.0490P.
5. Best, M.J.; Chakravarti N. (1990). "Active set algorithms for isotonic regression; a unifying framework". Mathematical Programming. 47 (1–3): 425–439. doi:10.1007/BF01580873.

Further reading

• Robertson, T.; Wright, F. T.; Dykstra, R. L. (1988). Order restricted statistical inference. New York: Wiley. ISBN 978-0-471-91787-8.
• Barlow, R. E.; Bartholomew, D. J.; Bremner, J. M.; Brunk, H. D. (1972). Statistical inference under order restrictions; the theory and application of isotonic regression. New York: Wiley. ISBN 978-0-471-04970-8.
• Shively, T.S., Sager, T.W., Walker, S.G. (2009). "A Bayesian approach to non-parametric monotone function estimation". Journal of the Royal Statistical Society, Series B. 71 (1): 159–175. CiteSeerX 10.1.1.338.3846. doi:10.1111/j.1467-9868.2008.00677.x.CS1 maint: multiple names: authors list (link)
• Wu, W. B.; Woodroofe, M.; Mentz, G. (2001). "Isotonic regression: Another look at the changepoint problem". Biometrika. 88 (3): 793–804. doi:10.1093/biomet/88.3.793.