Nonlinear mixed-effects model

Nonlinear mixed-effects models constitue a class of statistical models generalizing linear mixed-effects models. Like linear mixed-effects models, they are particularly useful in settings where there are multiple measurements within the same statistical units or when there are dependencies between measurements on related statistical units. Nonlinear mixed-effects models are applied in many fields including medicine, public health, pharmacology, and ecology.[1][2]

Definition

While any statistical model containing both fixed effects and random effects is an example of a nonlinear mixed-effects model, the most commonly used models are members of the class of nonlinear mixed-effects models for repeated measures[1]

${\displaystyle {y}_{ij}=f(\phi _{ij},{v}_{ij})+\epsilon _{ij},\quad i=1,\ldots ,M,\,j=1,\ldots ,n_{i}}$

where

• ${\displaystyle M}$ is the number of groups/subjects,
• ${\displaystyle n_{i}}$ is the number of observations for the ${\displaystyle i}$th group/subject,
• ${\displaystyle f}$ is a real-valued differentiable function of a group-specific parameter vector ${\displaystyle \theta _{ij}}$ and a covariate vector ${\displaystyle v_{ij}}$,
• ${\displaystyle \phi _{ij}}$ is modeled as a linear mixed-effects model ${\displaystyle \phi _{ij}={\boldsymbol {A}}_{ij}\beta +{\boldsymbol {B}}_{ij}{\boldsymbol {b}}_{i},}$ where ${\displaystyle \beta }$ is a vector of fixed effects and ${\displaystyle {\boldsymbol {b}}_{i}}$ is a vector of random effects associated with group ${\displaystyle i}$, and
• ${\displaystyle \epsilon _{ij}}$ is a random variable describing additive noise.

Estimation

When the model is only nonlinear in fixed effects and the random effects are Gaussian, maximum-likelihood estimation can be done using nonlinear least squares methods, although asymptotic properties of estimators and test statistics may differ from the conventional general linear model. In the more general setting, there exist several methods for doing maximum-likelihood estimation or maximum a posteriori estimation in certain classes of nonlinear mixed-effects models – typically under the assumption of normally distributed random variables. A popular approach is the Lindstrom-Bates algorithm[3] which relies on iteratively optimizing a nonlinear problem, locally linearizing the model around this optimum and then employing conventional methods from linear mixed-effects models to do maximum likelihood estimation. Stochastic approximation of the expectation-maximization algorithm gives an alternative approach for doing maximum-likelihood estimation.[4]

Applications

Disease progression modeling

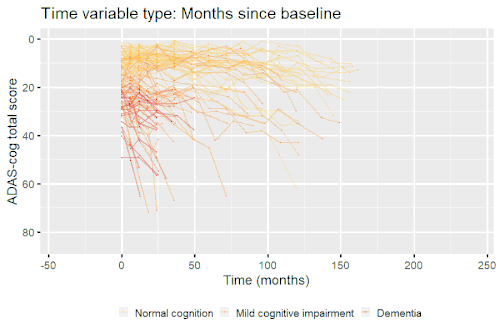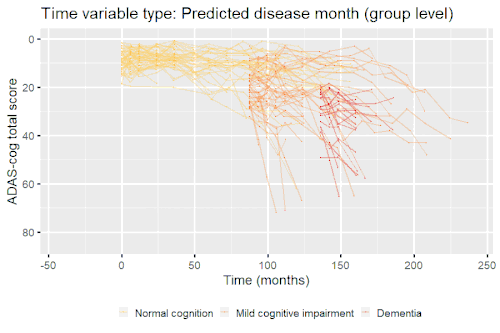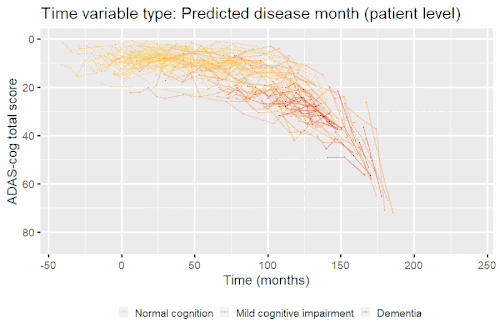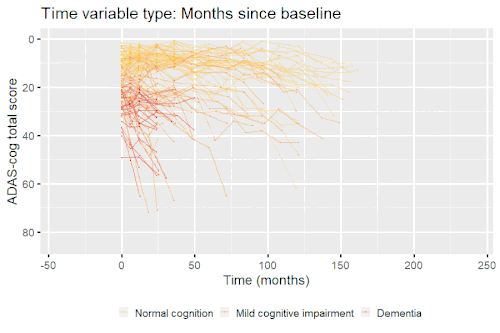
Nonlinear mixed-effects models have been used for modeling progression of disease.[5] In progressive disease, the temporal patterns of progression on outcome variables may follow a nonlinear temporal shape that is similar between patients. However, the stage of disease of an individual may not be known or only partially known from what can be measured. Therefore, a latent time variable that describe individual disease stage (i.e. where the patient is along the nonlinear mean curve) can be included in the model.

Example: Modeling cognitive decline in Alzheimer's disease

Example of disease progression modeling of longitudinal ADAS-Cog scores using the progmod R package.[5]

Alzheimer's disease is characterized by a progressive cognitive deterioration. However, patients may differ widely in cognitive ability and reserve, so cognitive testing at a single time point can often only be used to coarsely group individuals in different stages of disease. Now suppose we have a set of longitudinal cognitive data ${\displaystyle (y_{i1},\ldots ,y_{in_{i}})}$ from ${\displaystyle i=1,\ldots ,M}$ individuals that are each categorized as having either normal cognition (CN), mild cognitive impairment (MCI) or dementia (DEM) at the baseline visit (time ${\displaystyle t_{i1}=0}$ corresponding to measurement ${\displaystyle y_{i1}}$). These longitudinal trajectories can be modeled using a nonlinear mixed effects model that allows differences in disease state based on baseline categorization:

${\displaystyle {y}_{ij}=f_{\tilde {\beta }}(t_{ij}+A_{i}^{MCI}\beta ^{MCI}+A_{i}^{DEM}\beta ^{DEM}+b_{i})+\epsilon _{ij},\quad i=1,\ldots ,M,\,j=1,\ldots ,n_{i}}$

where

• ${\displaystyle f_{\tilde {\beta }}}$ is a function that models the mean time-profile of cognitive decline whose shape is determined by the parameters ${\displaystyle {\tilde {\beta }}}$,
• ${\displaystyle t_{ij}}$ represents observation time (e.g. time since baseline in the study),
• ${\displaystyle A_{i}^{MCI}}$ and ${\displaystyle A_{i}^{DEM}}$ are dummy variables that are 1 if individual ${\displaystyle i}$ has MCI or dementia at baseline and 0 otherwise,
• ${\displaystyle \beta ^{MCI}}$ and ${\displaystyle \beta ^{DEM}}$ are parameters that model the difference in disease progression of the MCI and dementia groups relative to the cognitively normal,
• ${\displaystyle b_{i}}$ is the difference in disease stage of individual ${\displaystyle i}$ relative to his/her baseline category, and
• ${\displaystyle \epsilon _{ij}}$ is a random variable describing additive noise.

An example of such a model with an exponential mean function fitted to longitudinal measurements of the Alzheimer's Disease Assessment Scale-Cognitive Subscale (ADAS-Cog) in shown in the box. As shown, the inclusion of fixed effects of baseline categorization (MCI or dementia relative to normal cognition) and the random effect of individual continuous disease stage ${\displaystyle b_{i}}$ aligns the trajectories of cognitive deterioration to reveal a common pattern of cognitive decline.

Growth analysis

Estimation of a mean height curve for boys from the Berkeley Growth Study with and without warping. Warping model is fitted as a nonlinear mixed-effects model using the pavpop R package.[6]

Growth phenomena often follow nonlinear patters (e.g. logistic growth, exponential growth, and hyperbolic growth). Factors such as nutrient deficiency may both directly affect the measured outcome (e.g. organisms with lack of nutrients end up smaller), but possibly also timing (e.g. organisms with lack of nutrients grow at a slower pace). If a model fails to account for the differences in timing, the estimated population-level curves may smooth out finer details due to lack of synchronization between organisms. Nonlinear mixed-effects models enable simultaneous modeling of individual differences in growth outcomes and timing.

Example: Modeling human height

Models for estimating the mean curves of human height and weight as a function of age and the natural variation around the mean are used to create growth charts. The growth of children can however become desynchronized due to both genetic and environmental factors. For example, age at onset of puberty and its associated height spurt can vary several years between adolescents. Therefore, cross-sectional studies may underestimate the magnitude of the pubertal height spurt because age is not synchronized with biological development. The differences in biological development can be modeled using random effects ${\displaystyle {\boldsymbol {w}}_{i}}$ that describe a mapping of observed age to a latent biological age using a so-called warping function ${\displaystyle v(\cdot ,{\boldsymbol {w}}_{i})}$. A simple nonlinear mixed-effects model with this structure is given by

${\displaystyle {y}_{ij}=f_{\beta }(v(t_{ij},{\boldsymbol {w}}_{i}))+\epsilon _{ij},\quad i=1,\ldots ,M,\,j=1,\ldots ,n_{i}}$

where

• ${\displaystyle f_{\beta }}$ is a function that represents the height development of a typical child as a function of age. Its shape is determined by the parameters ${\displaystyle \beta }$,
• ${\displaystyle t_{ij}}$ is the age of child ${\displaystyle i}$ corresponding to the height measurement ${\displaystyle y_{ij}}$,
• ${\displaystyle v(\cdot ,{\boldsymbol {w}}_{i})}$ is a warping function that maps age to biological development to synchronize. Its shape is determined by the random effects \boldsymbol{w}_i,
• ${\displaystyle \epsilon _{ij}}$ is a random variable describing additive variation (e.g. consistent differences in height between children and measurement noise).

There exists several methods and software packages for fitting such models. The so-called SITAR model[7] can fit such models using warping functions that are affine transformations of time (i.e. additive shifts in biological age and differences in rate of maturation), while the so-called pavpop model[6] can fit models with smoothly-varying warping functions. An example of the latter is shown in the box.

Pharmacokinetic/pharmacodynamic modeling

Basic pharmacokinetic processes affecting the fate of ingested substances. Nonlinear mixed-effects modeling can be used to estimate the population-level effects of these processes while also modeling the individual variation between subjects.

PK/PD models for describing exposure-response relationships such as the Emax model can be formulated as nonlinear mixed-effects models.[8] The mixed-model approach allows modeling of both population level and individual differences in effects that have a nonlinear effect on the observed outcomes, for example the rate at which a compound is being metabolized or distributed in the body.

See also

• Mixed model
• Fixed effects model
• Generalized linear mixed model
• Linear regression
• Mixed-design analysis of variance
• Multilevel model
• Random effects model
• Repeated measures design

References

1. Pinheiro, J; Bates, DM (2006). Mixed-effects models in S and S-PLUS. New York: Springer Science & Business Media.
2. Bolker, BM (2008). Ecological models and data in R. McMaster University: Mathematics & Statistics. Princeton University Press;.CS1 maint: extra punctuation (link)
3. Lindstrom, MJ; Bates, DM (1990). "Nonlinear mixed effects models for repeated measures data". Biometrics. 46 (3): 673–687.
4. Kuhn, E; Lavielle, M (2005). "Maximum likelihood estimation in nonlinear mixed effects models". Computational statistics & data analysis. 49 (4): 1020–1038. doi:10.1016/j.csda.2004.07.002.
5. Raket, LL (2020). "Statistical disease progression modeling in Alzheimer's disease". Frontiers in Big Data. doi:10.3389/fdata.2020.00024.
6. Raket LL, Sommer S, Markussen B (2014). "A nonlinear mixed-effects model for simultaneous smoothing and registration of functional data". Pattern Recognition Letters. 38: 1–7. doi:10.1016/j.patrec.2013.10.018.
7. Cole TJ, Donaldson MD, Ben-Shlomo Y (2010). "SITAR—a useful instrument for growth curve analysis". International journal of epidemiology. 39 (6): 1558–66. doi:10.1093/ije/dyq115.
8. Jonsson, EN; Karlsson, MO; Wade, JR (2000). "Nonlinearity detection: advantages of nonlinear mixed-effects modeling". Aaps Pharmsci.