Introduction to electromagnetism
Electromagnetism is one of the fundamental forces of nature. Early on, electricity and magnetism were studied separately and regarded as separate phenomena. Hans Christian Ørsted discovered that the two were related – electric currents give rise to magnetism. Michael Faraday discovered the converse, that magnetism could induce electric currents, and James Clerk Maxwell put the whole thing together in a unified theory of electromagnetism. Maxwell's equations further indicated that electromagnetic waves existed, and the experiments of Heinrich Hertz confirmed this, making radio possible. Maxwell also postulated, correctly, that light was a form of electromagnetic wave, thus making all of optics a branch of electromagnetism. Radio waves differ from light only in that the wavelength of the former is much longer than the latter. Albert Einstein showed that the magnetic field arises through the relativistic motion of the electric field and thus magnetism is merely a side effect of electricity. The modern theoretical treatment of electromagnetism is as a quantum field in quantum electrodynamics.
In many situations of interest to electrical engineering, it is not necessary to apply quantum theory to get correct results. Classical physics is still an accurate approximation in most situations involving macroscopic objects. With few exceptions, quantum theory is only necessary at the atomic scale and a simpler classical treatment can be applied. Further simplifications of treatment are possible in limited situations. Electrostatics deals only with stationary electric charges so magnetic fields do not arise and are not considered. Permanent magnets can be described without reference to electricity or electromagnetism. Circuit theory deals with electrical networks where the fields are largely confined around current carrying conductors. In such circuits, even Maxwell's equations can be dispensed with and simpler formulations used. On the other hand, a quantum treatment of electromagnetism is important in chemistry. Chemical reactions and chemical bonding are the result of quantum mechanical interactions of electrons around atoms. Quantum considerations are also necessary to explain the behaviour of many electronic devices, for instance the tunnel diode.
Electric charge
Electric charge is a quantity used to determine how a particle will behave in an electric field. There are three possible "types" of charge: positive, negative, and neutral. However, the distinction between positive and negative is by convention only.[1] Electric charge is quantized in units of the elementary charge, , where a proton has a charge of and an electron has a charge of . The SI unit of charge is the coulomb.[2]
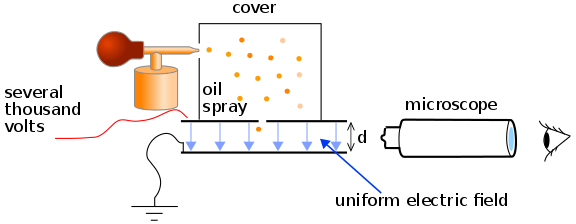
The elementary charge was first measured by Robert Millikan in his oil drop experiment in which the electric force on the particle is set to exactly counter the gravitational force that pulls it down, and the terminal velocity of this particle can be used to calculate its charge.[3] A neutron has no electric charge.
Charge conservation states that the overall electric charge in a closed system cannot change. Research suggests that the overall charge in the universe is neutral.[4][5]
Electric field
Electric force
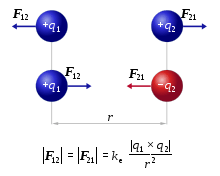
Coulomb's law states that the force on a charged particle due to the field from another particle is dependent on the magnitudes of the two charges as well as the distance between them.[6] The further away the particle is, the weaker the force on it is. Positive charges exert attractive forces on negative charges (and vice versa) while positive charges exert repulsive forces on other positive charges (and similarly for the force between negative charges). The SI units of force are newtons (N).[2]
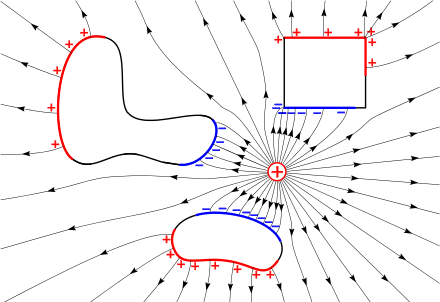
Field lines
Michael Faraday and James Clerk Maxwell, first introduced the concept of a field in his 1831 paper on electromagnetic induction, (called "lines of magnetic and electric force" in this publication):
"...by line of magnetic force, or magnetic line of force, or magnetic curve, I mean that exercise of magnetic force which is exerted in the lines usually called magnetic curves, and which equally exist as passing from or to magnetic poles, or forming concentric circles round an electric current. By line of electric force, I mean the force exerted in the lines joining two bodies, acting on each other according to the principles of static electric induction."[7]
Certain conventions are followed when drawing and interpreting electric field lines:[8]
- Electric field lines start at positive charges and end at negative charges;
- The density of the field lines corresponds to the strength of the field in that area and thus to the strength of the charge;
- The lines never cross, since otherwise the field would be pointing in two directions in one location; and
- The vector arrow represents the motion that a positive charge would undergo if placed in the field, while a negative charge would follow the direction opposite the arrow.
The SI unit of the electric field is volt per meter (V/m), or equivalently, newton per coulomb (N/C).[2] In mathematical expressions it is often represented as a vector-valued function . The electric field can be calculated in many ways, including Gauss' law, Coulomb's law, or Maxwell's equations. The electric field can also be interpreted as the electric force per unit charge.[9]
Electric flux

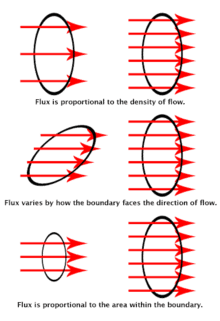
Flux can be thought of as the flow of the electric or magnetic field through a surface.[10] Fields can be represented by flux lines. Flux is analogous to the flow of a fluid through a surface since the angle of the surface to the direction of flow determines how much fluid can flow through the surface.[11] Gauss' law states that the flux through a closed surface is proportional to the amount of charge enclosed.[12] The SI units of flux are newton meters-squared per coulomb (), or equivalently, volt-meters (V m).[2]
Electric potential
Potential energy
The electric potential energy of a system of charges is the work it takes to assemble that configuration of charges.[6] The energies add pairwise; that is, the work to bring a third charge into a system of two charges is the energy associated with the first and third charge plus that associated with the second and third charge. The potential energy of the system is unique to the configuration itself.[13] The SI unit of energy is the joule (J).[2]
Equivalently, it may be thought of as the energy stored in the electric field.[14] For instance, if one were to hold two like charges a certain distance away from one another and then release them, the charges would move away with kinetic energy equal to the energy stored in the configuration. As an analogy, if one were to lift up a mass to a certain height in a gravitational field, the work it took to do so is equal to the energy stored in that configuration, and the kinetic energy of the mass upon contact with the ground would be equal to the energy of the configuration beforehand.[15]
Potential
The electric potential is the potential energy per unit charge.[16] The SI unit of electric potential is the volt (V).[2] The potential difference between two points determines the behavior of a particle. Positive charges move from high potentials to low potentials, whereas negative charges move from low to high potential. This may be thought of in terms of fluid flow. Take two identical containers filled with a fluid to unequal volumes. One container is at a higher level (potential) while the other container is at a lower level (potential). If connected by a pipe (a wire), the fluid (charge) would flow from the left container to the right container until the fluid heights (potentials) are equal. Mathematically, the potential is the line integral of the electric field. The electric field can be represented as the change in the potential with respect to distance.
Conductors and insulators
Conductors
A conductor is a material that allows electrons to flow easily. The most effective conductors are usually metals because their electrons can move around freely. This is described in the electron sea model of bonding in which electrons delocalize from the nuclei, leaving positive ions behind while the electrons are shared by all atoms in the lattice. Examples of good conductors include copper, aluminum, and silver. Wires in electronics are often made of copper.
The main tenets of conductors are as follows:[17]
- The electric field is zero inside a conductor. This is because charges are free to move and thus when they are disturbed by a field due to some external (or internal charge), they rearrange themselves such that the field that their configuration produces exactly cancels that caused by the source charge.
- The electric potential is the same everywhere inside the conductor and is constant across the surface of the conductor. This follows from the first statement because the field is zero everywhere inside the conductor and therefore the potential is not changing with distance inside the conductor.
- The electric field is perpendicular to the surface of a conductor. If this were not the case, the field would have a nonzero component on the surface of the conductor, which would cause the charges in the conductor to move around until that component of the field is zero.
- The net electric flux through a surface is proportional to the charge enclosed by the surface. This is a restatement of Gauss' law.
Semiconductors are materials that, depending on their temperature, become better or worse conductors.[18] Germanium and silicon are examples of semiconductors.
Superconductors are materials that exhibit little to no resistance to the flow of electrons when cooled below a certain temperature.[19]
Insulators
An insulator is a material with electrons that are more tightly bound and thus not able to move as freely as those of conductors. Insulators are often used to cover conducting wires so that charge will stay on the wire and will not go elsewhere.
Charge can be distributed inside an insulator thus the electric field inside an insulator is not necessarily zero.[20] Examples of insulators are plastics and polymers.
Magnetic field and force
Magnetic field
The magnetic field is that which arises from moving charges, currents, and magnetic objects. The field is represented mathematically as a vector-valued function . The SI unit of the magnetic field is the tesla (T).[2]
The magnetic field can be derived mathematically using Ampère's law, the Biot–Savart law, or Maxwell's equations.
Magnetic field lines have a very similar representation to electric field lines. There is an analogous notion of magnetic flux.[21] Magnetic field lines begin at north poles and end at south poles, and cannot cross. Magnetic fields arise due to the motion of charges, and also due to the alignment of the domains of magnetic materials where the magnetic moments of the atoms point in the same direction.[22]

The modern (post-Einstein) interpretation is that the magnetic field is equivalent to the electric field, but in a different reference frame.[23][24] Since magnetic fields can be interpreted as electric fields in a different reference frame (and vice versa), special relativity connects the two fields. One postulate of special relativity is length contraction, and because of that, the charge density in the wire increases, so a current-carrying wire viewed in a moving reference frame experiences a length-contracted coulomb force as compared to the wire in a stationary frame.[25] This force is called the magnetic force, and the associated field is the magnetic field. The direction of the magnetic force can be derived from the right-hand rule such that the force is perpendicular to both the direction of motion of the current (or charged particle) and the magnetic field.
Magnets
Permanent magnets make their own magnetic field. An example of a material from which a permanent magnet can be made is iron. It has a north and south pole, and cannot be split into a monopole — in other words, a north pole does not exist without a south pole.[26][27]
Electrons moving around atoms can create a magnetic field if their effects sum up constructively.[28] For magnetic materials like iron, the magnetic fields of the electrons moving around the nucleus add up, while for non-magnetic materials the effects average out to zero net magnetic field.[29]
Inductance
Inductance is the ability of an object to resist a change in current. From Ampère's law one can conclude that the magnetic field within a coil of wire (also called a solenoid) is constant inside the coil and zero outside the coil.[28] This property is useful in circuits to store energy within a magnetic field.
Inductors resist change in currents, therefore it will produce a current opposing the change. This is also known as Lenz's law. Because of this property, inductors oppose alternating current.[30]
Circuits
Circuits are connections of electrical components. Common components are as follows:
| Component | Main function | Schematic symbol |
|---|---|---|
| Resistor | Impedes the flow of current | |
| Battery | Acts as a power source | 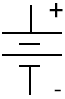 |
| Capacitor | Stores energy in electric fields, stores charge, passes low frequency alternating current | 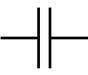 |
| Inductor | Stores energy in magnetic fields, resists change in current |
Current is defined as the change of charge per unit time, often represented as and in units of amperes (A). Voltage is the difference in electric potential between two points in the circuit. In batteries, the potential difference is often called the emf (electromotive force) and is in units volt (V).
Ohm's law states a relationship among the current, the voltage, and the resistance of a circuit: the current that flows is proportional to the voltage and inversely proportional to the resistance.
Direct current (DC) is constant current that flows in one direction. Alternating current (AC) is a current that switches direction according to a sinusoidal function, typically. Power grids use alternating current, and so residences and appliances are generally powered by AC.
Kirchhoff's junction rule
Kirchhoff's junction rule states that the current going into a junction (or node) must equal the current that leaves the node.[31] This comes from charge conservation, as current is defined as the flow of charge over time.
If a current splits as it exits a junction, the sum of the resultant split currents is equal to the incoming circuit.
Kirchhoff's loop rule
Kirchhoff's loop rule states that the sum of the voltage drops in a closed loop around a circuit equals zero.[32] This comes from the conservation of energy, as voltage is defined as the energy per unit charge.
Parallel versus series
Components are said to be in parallel when the voltage drops across one branch is equal to that across another. Components are said to be in series when the current through one component is equal to that through another. Thus, the voltages across each path in a parallel circuit is the same, and the current through each component in a series circuit is the same.
Equivalent resistance in series is given by for resistors in series, while equivalent resistance in parallel is given by for resistors in parallel.
Equivalent capacitance in series is given by , while equivalent capacitance in parallel is given by .
Electromagnetic waves
Electromagnetic waves are a result of Maxwell's equations which, in part, state that changing electric fields produce magnetic fields and vice versa. Due to this dependence, the fields form an electromagnetic wave, also called electromagnetic radiation (EMR). The electric and magnetic fields are perpendicular to each other, and to the direction of propagation of the electromagnetic wave.
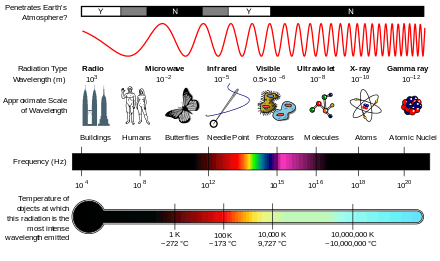
Visible light is a form of electromagnetic radiation. The speed of propagation of electromagnetic waves calculated from Maxwell's equations is identical to the measured speed of light. It was this result that led Maxwell to conclude that light is a form of electromagnetic radiation. Other forms include, in order of increasing wavelength, gamma rays, X-rays, ultraviolet, infrared, microwaves, and radio waves.
References
- Purcell, Edward M. (2013). Electricity and Magnetism, Third Edition. Cambridge: Cambridge University Press. pp. 2–4. ISBN 978-1107014022.
- International Bureau of Weights and Measures (2006), The International System of Units (SI) (PDF) (8th ed.), ISBN 92-822-2213-6, archived (PDF) from the original on 2017-08-14.
- , Millikan discussing his work and subsequent improvements.
- S. Orito; M. Yoshimura (1985). "Can the Universe be Charged?". Physical Review Letters. 54 (22): 2457–60. Bibcode: 1985PhRvL..54.2457O. doi:10.1103/PhysRevLett.54.2457. PMID 10031347.
- E. Masso; F. Rota (2002). "Primordial helium production in a charged universe". Physics Letters B. 545 (3–4): 221–25. arXiv:astro-ph/0201248. Bibcode: 2002PhLB..545..221M. doi:10.1016/S0370-2693(02)02636-9.
- Halliday, David; Resnick, Robert (2011). Fundamentals of Physics, 9th ed. Jefferson City: John Wiley & Sons, Inc. pp. 628–31. ISBN 978-0470469088.
- Assis, Andre & Ribeiro, A & Vannucci, A. (2009). The field concepts of Faraday and Maxwell. 34.
- Pumplin, Jon (2000). "Electric field lines". Michigan State University Physics. Retrieved 18 October 2018.
- Nave, R. "Electric Field". Georgia State University Hyperphysics. Retrieved 16 October 2018.
- Purcell, Edward M. (2013-01-21). Electricity and magnetism (Third ed.). Cambridge. pp. 22–24. ISBN 978-1107014022. OCLC 805015622.
- "The Feynman Lectures on Physics Vol. II Ch. 3: Vector Integral Calculus". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- "Gauss's Law". hyperphysics.phy-astr.gsu.edu. Retrieved 2018-10-30.
- Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. pp. 13–14. ISBN 978-1107014022. OCLC 805015622.
- PurcellM., Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. pp. 33–34. ISBN 978-1107014022. OCLC 805015622.
- MacIsaac, Dan; Saeli, Susan (February 2007). "Using Gravitational Analogies to Introduce Elementary Electrical Field Theory Concepts" (PDF). The Physics Teacher. 45 (2): 104–08. Bibcode:2007PhTea..45..104S. doi:10.1119/1.2432088. Retrieved 30 October 2018.
- "The Feynman Lectures on Physics Vol. II Ch. 4: Electrostatics". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. p. 129. ISBN 978-1107014022. OCLC 805015622.
- "The Feynman Lectures on Physics Vol. III Ch. 14: Semiconductors". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- "The Feynman Lectures on Physics Vol. III Ch. 21: The Schrödinger Equation in a Classical Context: A Seminar on Superconductivity". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- Evans, Martin (7 September 2013). "Gauss' Law" (PDF). University of Edinburgh School of Astronomy and Physics. Retrieved 30 October 2018.
- Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. p. 348. ISBN 978-1107014022. OCLC 805015622.
- "The Feynman Lectures on Physics Vol. II Ch. 1: Electromagnetism". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. pp. 235–68. ISBN 978-1107014022. OCLC 805015622.
- "The Feynman Lectures on Physics Vol. II Ch. 13: Magnetostatics". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- A. French (1968) Special Relativity, chapter 8 – Relativity and electricity, pp. 229–65, W.W. Norton.
- Hooper, Dan (October 6, 2009). "Dark Cosmos: In Search of Our Universe's Missing Mass and Energy". Harper Collins – via Google Books.
- "Particle Data Group summary of magnetic monopole search" (PDF). lbl.gov.
- "The Feynman Lectures on Physics Vol. II Ch. 13: Magnetostatics". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- Purcell, Edward M. (2013). Electricity and magnetism (Third ed.). Cambridge. pp. 540–49. ISBN 978-1107014022. OCLC 805015622.
- "The Feynman Lectures on Physics Vol. II Ch. 17: The Laws of Induction". www.feynmanlectures.caltech.edu. Retrieved 2018-10-30.
- Walker, Jearl (2011). Fundamentals of physics. Halliday, David; Resnick, Robert (9th ed.). Hoboken, NJ: Wiley. pp. 710–12. ISBN 978-0470469118. OCLC 435710913.
- Walker, Jearl (2011). Fundamentals of physics. Halliday, David; Resnick, Robert (9th ed.). Hoboken, NJ: Wiley. pp. 682–700. ISBN 9780470469118. OCLC 435710913.