Compound of four octahedra
The compound of four octahedra is a uniform polyhedron compound. It's composed of a symmetric arrangement of 4 octahedra, considered as triangular antiprisms. It can be constructed by superimposing four identical octahedra, and then rotating each by 60 degrees about a separate axis (that passes through the centres of two opposite octahedral faces).
| Compound of four octahedra | |
|---|---|
 | |
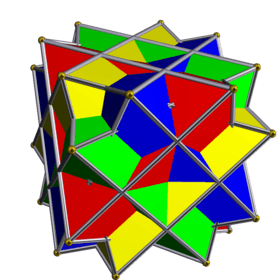| Type | Uniform compound |
| Index | UC12 |
| Convex hull | Nonuniform truncated cube |
| Polyhedra | 4 octahedra |
| Faces | 8+24 triangles |
| Edges | 48 |
| Vertices | 24 |
| Symmetry group | octahedral (Oh) |
| Subgroup restricting to one constituent | 3-fold antiprismatic (D3d) |
3D model of a compound of four octahedra
Its dual is the compound of four cubes.
Cartesian coordinates
Cartesian coordinates for the vertices of this compound are all the permutations of
- (±2, ±1, ±2)
gollark: Provably or probably?
gollark: Palaiologos age reveal is 3 unlikely.
gollark: LyricLy (time domain plot).
gollark: Atmospheric bee concentrations are really high nowadays.
gollark: If only the osmarks.tk™ secondary server ran on bees instead of electrons.
See also
References
- Skilling, John (1976), "Uniform Compounds of Uniform Polyhedra", Mathematical Proceedings of the Cambridge Philosophical Society, 79 (03): 447–457, doi:10.1017/S0305004100052440, MR 0397554.
This article is issued from Wikipedia. The text is licensed under Creative Commons - Attribution - Sharealike. Additional terms may apply for the media files.