Vector calculus identities

The following are important identities involving derivatives and integrals in vector calculus.

See also: Vector algebra relations

Operator notation

Gradient

Main article: Gradient

For a function ${\displaystyle f(x,y,z)}$ in three-dimensional Cartesian coordinate variables, the gradient is the vector field:

${\displaystyle \operatorname {grad} (f)=\nabla f={\begin{pmatrix}{\frac {\partial }{\partial x}},\ {\frac {\partial }{\partial y}},\ {\frac {\partial }{\partial z}}\end{pmatrix}}f={\frac {\partial f}{\partial x}}\mathbf {i} +{\frac {\partial f}{\partial y}}\mathbf {j} +{\frac {\partial f}{\partial z}}\mathbf {k} }$

where i, j, k are the standard unit vectors for the x, y, z-axes. More generally, for a function of n variables ${\displaystyle \psi (x_{1},\ldots ,x_{n})}$, also called a scalar field, the gradient is the vector field:

${\displaystyle \nabla \psi ={\begin{pmatrix}{\frac {\partial }{\partial x_{1}}},\ldots ,\ {\frac {\partial }{\partial x_{n}}}\end{pmatrix}}\psi ={\frac {\partial \psi }{\partial x_{1}}}\mathbf {e} _{1}+\ldots +{\frac {\partial \psi }{\partial x_{n}}}\mathbf {e} _{n}.}$

where ${\displaystyle \mathbf {e} _{i}}$ are orthogonal unit vectors in arbitrary directions.

For a vector field ${\displaystyle \mathbf {A} =\left(A_{1},\ldots ,A_{n}\right)}$ written as a 1 × n row vector, also called a tensor field of order 1, the gradient or covariant derivative is the n × n Jacobian matrix:

${\displaystyle \nabla \!\mathbf {A} =\mathbf {J} _{\mathbf {A} }=\left({\frac {\partial A_{i}}{\partial x_{j}}}\right)_{\!ij}.}$

For a tensor field ${\displaystyle \mathbf {A} }$ of any order k, the gradient ${\displaystyle \operatorname {grad} (\mathbf {A} )=\nabla \!\mathbf {A} }$ is a tensor field of order k + 1.

Divergence

Main article: Divergence

In Cartesian coordinates, the divergence of a continuously differentiable vector field ${\displaystyle \mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k} }$ is the scalar-valued function:

${\displaystyle \operatorname {div} \mathbf {F} =\nabla \cdot \mathbf {F} ={\begin{pmatrix}{\frac {\partial }{\partial x}},\ {\frac {\partial }{\partial y}},\ {\frac {\partial }{\partial z}}\end{pmatrix}}\cdot {\begin{pmatrix}F_{x},\ F_{y},\ F_{z}\end{pmatrix}}={\frac {\partial F_{x}}{\partial x}}+{\frac {\partial F_{y}}{\partial y}}+{\frac {\partial F_{z}}{\partial z}}.}$

The divergence of a tensor field ${\displaystyle \mathbf {A} }$ of non-zero order k is written as ${\displaystyle \operatorname {div} (\mathbf {A} )=\nabla \cdot \mathbf {A} }$, a contraction to a tensor field of order k − 1. Specifically, the divergence of a vector is a scalar. The divergence of a higher order tensor field may be found by decomposing the tensor field into a sum of outer products and using the identity,

${\displaystyle \nabla \cdot \left(\mathbf {B} \otimes {\hat {\mathbf {A} }}\right)={\hat {\mathbf {A} }}(\nabla \cdot \mathbf {B} )+(\mathbf {B} \cdot \nabla ){\hat {\mathbf {A} }}}$

where ${\displaystyle \mathbf {B} \cdot \nabla }$ is the directional derivative in the direction of ${\displaystyle \mathbf {B} }$ multiplied by its magnitude. Specifically, for the outer product of two vectors,

${\displaystyle \nabla \cdot \left(\mathbf {b} \mathbf {a} ^{\mathsf {T}}\right)=\mathbf {a} \left(\nabla \cdot \mathbf {b} \right)+\left(\mathbf {b} \cdot \nabla \right)\mathbf {a} .}$

Curl

Main article: Curl (mathematics)

In Cartesian coordinates, for ${\displaystyle \mathbf {F} =F_{x}\mathbf {i} +F_{y}\mathbf {j} +F_{z}\mathbf {k} }$ the curl is the vector field:

${\displaystyle \operatorname {curl} \mathbf {F} =\nabla \times \mathbf {F} ={\begin{pmatrix}{\frac {\partial }{\partial x}},\ {\frac {\partial }{\partial y}},\ {\frac {\partial }{\partial z}}\end{pmatrix}}\times {\begin{pmatrix}F_{x},\ F_{y},\ F_{z}\end{pmatrix}}=\left|{\begin{matrix}\mathbf {i} &\mathbf {j} &\mathbf {k} \\{\frac {\partial }{\partial x}}&{\frac {\partial }{\partial y}}&{\frac {\partial }{\partial z}}\\F_{x}&F_{y}&F_{z}\end{matrix}}\right|=\left({\frac {\partial F_{z}}{\partial y}}-{\frac {\partial F_{y}}{\partial z}}\right)\mathbf {i} +\left({\frac {\partial F_{x}}{\partial z}}-{\frac {\partial F_{z}}{\partial x}}\right)\mathbf {j} +\left({\frac {\partial F_{y}}{\partial x}}-{\frac {\partial F_{x}}{\partial y}}\right)\mathbf {k} }$

where i, j, and k are the unit vectors for the x-, y-, and z-axes, respectively. In Einstein notation, the vector field ${\displaystyle \mathbf {F} ={\begin{pmatrix}F_{1}&F_{2}&F_{3}\end{pmatrix}}}$has curl given by:

${\displaystyle \nabla \times \mathbf {F} =\varepsilon ^{ijk}\mathbf {e} _{i}{\frac {\partial F_{k}}{\partial x^{j}}}}$

where ${\displaystyle \varepsilon }$ = ±1 or 0 is the Levi-Civita parity symbol.

Laplacian

Main article: Laplace operator

In Cartesian coordinates, the Laplacian of a function ${\displaystyle f(x,y,z)}$ is

${\displaystyle \Delta f=\nabla ^{2}\!f=(\nabla \cdot \nabla )f={\frac {\partial ^{2}\!f}{\partial x^{2}}}+{\frac {\partial ^{2}\!f}{\partial y^{2}}}+{\frac {\partial ^{2}\!f}{\partial z^{2}}}.}$

For a tensor field, ${\displaystyle \mathbf {A} }$, the Laplacian is generally written as:

${\displaystyle \Delta \mathbf {A} =\nabla ^{2}\!\mathbf {A} =(\nabla \cdot \nabla )\mathbf {A} }$

and is a tensor field of the same order.

When the Laplacian is equal to 0, the function is called a Harmonic Function. That is,

${\displaystyle \Delta f=0}$

Special notations

In Feynman subscript notation,

${\displaystyle \nabla _{\mathbf {B} }\!\left(\mathbf {A{\cdot }B} \right)=\mathbf {A} {\times }\!\left(\nabla {\times }\mathbf {B} \right)+\left(\mathbf {A} {\cdot }\nabla \right)\mathbf {B} }$

where the notation ∇_B means the subscripted gradient operates on only the factor B.[1][2]

Less general but similar is the Hestenes overdot notation in geometric algebra.[3] The above identity is then expressed as:

${\displaystyle {\dot {\nabla }}\left(\mathbf {A} {\cdot }{\dot {\mathbf {B} }}\right)=\mathbf {A} {\times }\!\left(\nabla {\times }\mathbf {B} \right)+\left(\mathbf {A} {\cdot }\nabla \right)\mathbf {B} }$

where overdots define the scope of the vector derivative. The dotted vector, in this case B, is differentiated, while the (undotted) A is held constant.

For the remainder of this article, Feynman subscript notation will be used where appropriate.

First derivative identities

For scalar fields ${\displaystyle \psi }$, ${\displaystyle \phi }$ and vector fields ${\displaystyle \mathbf {A} }$, ${\displaystyle \mathbf {B} }$, we have the following derivative identities.

Distributive properties

${\displaystyle {\begin{aligned}\nabla (\psi +\phi )&=\nabla \psi +\nabla \phi \\\nabla (\mathbf {A} +\mathbf {B} )&=\nabla \mathbf {A} +\nabla \mathbf {B} \\\nabla \cdot (\mathbf {A} +\mathbf {B} )&=\nabla {\cdot }\mathbf {A} +\nabla \cdot \mathbf {B} \\\nabla \times (\mathbf {A} +\mathbf {B} )&=\nabla \times \mathbf {A} +\nabla \times \mathbf {B} \end{aligned}}}$

Product rule for multiplication by a scalar

We have the following generalizations of the product rule in single variable calculus.

${\displaystyle {\begin{aligned}\nabla (\psi \phi )&=\phi \,\nabla \psi +\psi \,\nabla \phi \\\nabla (\psi \mathbf {A} )&=(\nabla \psi )^{\mathbf {T} }\mathbf {A} +\psi \nabla \mathbf {A} \ =\ \nabla \psi \otimes \mathbf {A} +\psi \,\nabla \mathbf {A} \\\nabla \cdot (\psi \mathbf {A} )&=\psi \,\nabla {\cdot }\mathbf {A} +(\nabla \psi )\,{\cdot }\mathbf {A} \\\nabla {\times }(\psi \mathbf {A} )&=\psi \,\nabla {\times }\mathbf {A} +(\nabla \psi ){\times }\mathbf {A} \\\nabla ^{2}(fg)&=f\,\nabla ^{2\!}g+2\,\nabla \!f\cdot \!\nabla g+g\,\nabla ^{2\!}f\end{aligned}}}$

In the second formula, the transposed gradient ${\displaystyle (\nabla \psi )^{\mathbf {T} }}$ is an n × 1 column vector, ${\displaystyle \mathbf {A} }$ is a 1 × n row vector, and their product is an n × n matrix (or more precisely, a dyad); This may also be considered as the tensor product ${\displaystyle \otimes }$ of two vectors, or of a covector and a vector.

Quotient rule for division by a scalar

${\displaystyle {\begin{aligned}\nabla \left({\frac {\psi }{\phi }}\right)&={\frac {\phi \,\nabla \psi -\psi \,\nabla \phi }{\phi ^{2}}}\\[1em]\nabla \cdot \left({\frac {\mathbf {A} }{\phi }}\right)&={\frac {\phi \,\nabla {\cdot }\mathbf {A} -\nabla \!\phi \cdot \mathbf {A} }{\phi ^{2}}}\\[1em]\nabla \times \left({\frac {\mathbf {A} }{\phi }}\right)&={\frac {\phi \,\nabla {\times }\mathbf {A} -\nabla \!\phi \,{\times }\,\mathbf {A} }{\phi ^{2}}}\end{aligned}}}$

Chain rule

Let ${\displaystyle f(x)}$ be a one-variable function from scalars to scalars, ${\displaystyle \mathbf {r} (t)=(r_{1}(t),\ldots ,r_{n}(t))}$ a parametrized curve, and ${\displaystyle F:\mathbb {R} ^{n}\to \mathbb {R} }$ a function from vectors to scalars. We have the following special cases of the multi-variable chain rule.

${\displaystyle {\begin{aligned}\nabla (f\circ F)&=\left(f'\circ F\right)\,\nabla F\\(F\circ \mathbf {r} )'&=(\nabla F\circ \mathbf {r} )\cdot \mathbf {r} '\\\nabla (F\circ \mathbf {A} )&=(\nabla F\circ \mathbf {A} )\,\nabla \mathbf {A} \end{aligned}}}$

For a coordinate parametrization ${\displaystyle \Phi$ :\mathbb {R} ^{n}\to \mathbb {R} ^{n}} we have:

${\displaystyle \nabla \cdot (\mathbf {A} \circ \Phi )=\mathrm {tr} \left((\nabla \mathbf {A} \circ \Phi )\mathbf {J} _{\Phi }\right)}$

Here we take the trace of the product of two n × n matrices: the gradient of A and the Jacobian of ${\displaystyle \Phi }$.

Dot product rule

${\displaystyle {\begin{aligned}\nabla (\mathbf {A} \cdot \mathbf {B} )&\ =\ (\mathbf {A} \cdot \nabla )\mathbf {B} \,+\,(\mathbf {B} \cdot \nabla )\mathbf {A} \,+\,\mathbf {A} {\times }(\nabla {\times }\mathbf {B} )\,+\,\mathbf {B} {\times }(\nabla {\times }\mathbf {A} )\\&\ =\ \mathbf {A} \cdot \mathbf {J} _{\mathbf {B} }+\mathbf {B} \cdot \mathbf {J} _{\mathbf {A} }\ =\ \mathbf {A} \cdot \nabla \mathbf {B} \,+\,\mathbf {B} \cdot \nabla \!\mathbf {A} \end{aligned}}}$

where ${\displaystyle \mathbf {J} _{\mathbf {A} }=\nabla \!\mathbf {A} =(\partial A_{i}/\partial x_{j})_{ij}}$ denotes the Jacobian matrix of the vector field ${\displaystyle \mathbf {A} =(A_{1},\ldots ,A_{n})}$, and in the last expression the ${\displaystyle \cdot }$ operations are understood not to act on the ${\displaystyle \nabla }$ directions (which some authors would indicate by appropriate parentheses or transposes).

Alternatively, using Feynman subscript notation,

${\displaystyle \nabla (\mathbf {A} \cdot \mathbf {B} )=\nabla _{\mathbf {A} }(\mathbf {A} \cdot \mathbf {B} )+\nabla _{\mathbf {B} }(\mathbf {A} \cdot \mathbf {B} )\ .}$

See these notes.[4]

As a special case, when A = B,

${\displaystyle {\tfrac {1}{2}}\nabla \left(\mathbf {A} \cdot \mathbf {A} \right)\ =\ \mathbf {A} \cdot \mathbf {J} _{\mathbf {A} }\ =\ \mathbf {A} \cdot \nabla \mathbf {A} \ =\ (\mathbf {A} {\cdot }\nabla )\mathbf {A} \,+\,\mathbf {A} {\times }(\nabla {\times }\mathbf {A} ).}$

The generalization of the dot product formula to Riemannian manifolds is a defining property of a Riemannian connection, which differentiates a vector field to give a vector-valued 1-form.

Cross product rule

${\displaystyle {\begin{aligned}\nabla \cdot (\mathbf {A} \times \mathbf {B} )&\ =\ (\nabla {\times }\mathbf {A} )\cdot \mathbf {B} \,-\,\mathbf {A} \cdot (\nabla {\times }\mathbf {B} )\\[5pt]\nabla \times (\mathbf {A} \times \mathbf {B} )&\ =\ \mathbf {A} (\nabla {\cdot }\mathbf {B} )\,-\,\mathbf {B} (\nabla {\cdot }\mathbf {A} )\,+\,(\mathbf {B} {\cdot }\nabla )\mathbf {A} \,-\,(\mathbf {A} {\cdot }\nabla )\mathbf {B} \\[2pt]&\ =\ (\nabla {\cdot }\,\mathbf {B} \,+\,\mathbf {B} \,{\cdot }\nabla )\mathbf {A} \,-\,(\nabla {\cdot }\mathbf {A} \,+\,\mathbf {A} {\cdot }\nabla )\mathbf {B} \\[2pt]&\ =\ \nabla {\cdot }\left(\mathbf {B} \mathbf {A} ^{\mathrm {T} }\right)\,-\,\nabla {\cdot }\left(\mathbf {A} \mathbf {B} ^{\mathrm {T} }\right)\\[2pt]&\ =\ \nabla {\cdot }\left(\mathbf {B} \mathbf {A} ^{\mathrm {T} }\,-\,\mathbf {A} \mathbf {B} ^{\mathrm {T} }\right)\\\mathbf {A} \times (\nabla \times \mathbf {B} )&\ =\ \nabla _{\mathbf {B} }(\mathbf {A} {\cdot }\mathbf {B} )\,-\,(\mathbf {A} {\cdot }\nabla )\mathbf {B} \\[2pt]&\ =\ \mathbf {A} \cdot \mathbf {J} _{\mathbf {B} }\,-\,(\mathbf {A} {\cdot }\nabla )\mathbf {B} =\ \mathbf {A} \cdot \nabla \mathbf {B} \,-\,(\mathbf {A} {\cdot }\nabla )\mathbf {B} \\[5pt](\mathbf {A} \times \nabla )\times \mathbf {B} &\ =\ \mathbf {A} \cdot \nabla \mathbf {B} \,-\,\mathbf {A} (\nabla {\cdot }\mathbf {B} )\\&\ =\ \mathbf {A} \times (\nabla \times \mathbf {B} )\,+\,(\mathbf {A} {\cdot }\nabla )\mathbf {B} \,-\,\mathbf {A} (\nabla {\cdot }\mathbf {B} )\end{aligned}}}$

Note the difference between

${\displaystyle \mathbf {A} \cdot \nabla \mathbf {B} \ =\ \mathbf {A} \cdot \mathbf {J} _{\mathbf {B} }\ =\ A_{i}\left({\frac {\partial B_{i}}{\partial x_{j}}}\right)}$

and

${\displaystyle (\mathbf {A} \cdot \nabla )\mathbf {B} \ =\ \left(A_{i}{\frac {\partial }{\partial x_{i}}}\right)B_{j}=\ A_{i}\left({\frac {\partial B_{j}}{\partial x_{i}}}\right)\,.}$

Second derivative identities

Divergence of curl is zero

The divergence of the curl of any vector field A is always zero:

${\displaystyle \nabla \cdot (\nabla \times \mathbf {A} )=0}$

This is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.

Divergence of gradient is Laplacian

The Laplacian of a scalar field is the divergence of its gradient:

${\displaystyle \nabla ^{2}\psi =\nabla \cdot (\nabla \psi )}$

The result is a scalar quantity.

Divergence of divergence is undefined

Divergence of a vector field A is a scalar, and you cannot take the divergence of a scalar quantity. Therefore:

${\displaystyle \nabla \cdot (\nabla \cdot \mathbf {A} )={\text{undefined}}}$

Curl of gradient is zero

The curl of the gradient of any continuously twice-differentiable scalar field ${\displaystyle \ \phi }$ is always the zero vector:

${\displaystyle \nabla \times (\nabla \phi )=\mathbf {0} }$

This is a special case of the vanishing of the square of the exterior derivative in the De Rham chain complex.

Curl of curl

${\displaystyle \nabla \times \left(\nabla \times \mathbf {A} \right)\ =\ \nabla (\nabla {\cdot }\mathbf {A} )\,-\,\nabla ^{2\!}\mathbf {A} }$

Here ∇² is the vector Laplacian operating on the vector field A.

Curl of divergence is undefined

The divergence of a vector field A is a scalar, and you cannot take curl of a scalar quantity. Therefore

${\displaystyle \nabla \times (\nabla \cdot \mathbf {A} )\ {\text{is undefined}}}$

Summary of important identities

Differentiation

Gradient

• ${\displaystyle \nabla (\psi +\phi )=\nabla \psi +\nabla \phi }$
• ${\displaystyle \nabla (\psi \phi )=\phi \nabla \psi +\psi \nabla \phi }$
• ${\displaystyle \nabla (\psi \mathbf {A} )=\nabla \psi \otimes \mathbf {A} +\psi \nabla \mathbf {A} }$
• ${\displaystyle \nabla (\mathbf {A} \cdot \mathbf {B} )=(\mathbf {A} \cdot \nabla )\mathbf {B} +(\mathbf {B} \cdot \nabla )\mathbf {A} +\mathbf {A} \times (\nabla \times \mathbf {B} )+\mathbf {B} \times (\nabla \times \mathbf {A} )}$

Divergence

• ${\displaystyle \nabla \cdot (\mathbf {A} +\mathbf {B} )=\nabla \cdot \mathbf {A} +\nabla \cdot \mathbf {B} }$
• ${\displaystyle \nabla \cdot \left(\psi \mathbf {A} \right)=\psi \nabla \cdot \mathbf {A} +\mathbf {A} \cdot \nabla \psi }$
• ${\displaystyle \nabla \cdot \left(\mathbf {A} \times \mathbf {B} \right)=(\nabla \times \mathbf {A} )\cdot \mathbf {B} -(\nabla \times \mathbf {B} )\cdot \mathbf {A} }$

Curl

• ${\displaystyle \nabla \times (\mathbf {A} +\mathbf {B} )=\nabla \times \mathbf {A} +\nabla \times \mathbf {B} }$
• ${\displaystyle \nabla \times \left(\psi \mathbf {A} \right)=\psi \,(\nabla \times \mathbf {A} )+\nabla \psi \times \mathbf {A} }$
• ${\displaystyle \nabla \times \left(\psi \nabla \phi \right)=\nabla \psi \times \nabla \phi }$
• ${\displaystyle \nabla \times \left(\mathbf {A} \times \mathbf {B} \right)=\mathbf {A} \left(\nabla \cdot \mathbf {B} \right)-\mathbf {B} \left(\nabla \cdot \mathbf {A} \right)+\left(\mathbf {B} \cdot \nabla \right)\mathbf {A} -\left(\mathbf {A} \cdot \nabla \right)\mathbf {B} }$

Second derivatives

DCG chart: Some rules for second derivatives.

• ${\displaystyle \nabla \cdot (\nabla \times \mathbf {A} )=0}$
• ${\displaystyle \nabla \times (\nabla \psi )=\mathbf {0} }$
• ${\displaystyle \nabla \cdot (\nabla \psi )=\nabla ^{2}\psi }$ (scalar Laplacian)
• ${\displaystyle \nabla \left(\nabla \cdot \mathbf {A} \right)-\nabla \times \left(\nabla \times \mathbf {A} \right)=\nabla ^{2}\mathbf {A} }$ (vector Laplacian)
• ${\displaystyle \nabla \cdot (\phi \nabla \psi )=\phi \nabla ^{2}\psi +\nabla \phi \cdot \nabla \psi }$
• ${\displaystyle \psi \nabla ^{2}\phi -\phi \nabla ^{2}\psi =\nabla \cdot \left(\psi \nabla \phi -\phi \nabla \psi \right)}$
• ${\displaystyle \nabla ^{2}(\phi \psi )=\phi \nabla ^{2}\psi +2(\nabla \phi )\cdot (\nabla \psi )+\left(\nabla ^{2}\phi \right)\psi }$
• ${\displaystyle \nabla ^{2}(\psi \mathbf {A} )=\mathbf {A} \nabla ^{2}\psi +2(\nabla \psi \cdot \nabla )\mathbf {A} +\psi \nabla ^{2}\mathbf {A} }$
• ${\displaystyle \nabla ^{2}(\mathbf {A} \cdot \mathbf {B} )=\mathbf {A} \cdot \nabla ^{2}\mathbf {B} -\mathbf {B} \cdot \nabla ^{2}\!\mathbf {A} +2\nabla \cdot ((\mathbf {B} \cdot \nabla )\mathbf {A} +\mathbf {B} \times (\nabla \times \mathbf {A} ))}$ (Green's vector identity)

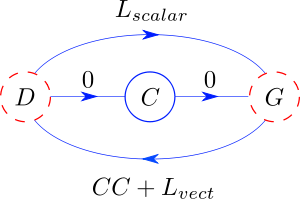
The figure to the right is a mnemonic for some of these identities. The abbreviations used are:

• D: divergence,
• C: curl,
• G: gradient,
• L: Laplacian,
• CC: curl of curl.

Each arrow is labeled with the result of an identity, specifically, the result of applying the operator at the arrow's tail to the operator at its head. The blue circle in the middle means curl of curl exists, whereas the other two red circles (dashed) mean that DD and GG do not exist.

Third derivatives

${\displaystyle {\begin{aligned}\nabla ^{2}(\nabla \psi )&=\nabla (\nabla \cdot (\nabla \psi ))=\nabla \left(\nabla ^{2}\psi \right)\\\nabla ^{2}(\nabla \cdot \mathbf {A} )&=\nabla \cdot (\nabla (\nabla \cdot \mathbf {A} ))=\nabla \cdot \left(\nabla ^{2}\mathbf {A} \right)\\\nabla ^{2}(\nabla \times \mathbf {A} )&=-\nabla \times (\nabla \times (\nabla \times \mathbf {A} ))=\nabla \times \left(\nabla ^{2}\mathbf {A} \right)\end{aligned}}}$

Integration

Below, the curly symbol ∂ means "boundary of" a surface or solid.

Surface–volume integrals

In the following surface–volume integral theorems, V denotes a three-dimensional volume with a corresponding two-dimensional boundary S = ∂V (a closed surface):

• ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \mathbf {A} \cdot d\mathbf {S} \ =\ \iiint _{V}\left(\nabla \cdot \mathbf {A} \right)dV}$ (divergence theorem)
• ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \psi \,d\mathbf {S} \ =\ \iiint _{V}\nabla \psi \,dV}$
• ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \mathbf {A} \times d\mathbf {S} \ =\ -\iiint _{V}\nabla \times \mathbf {A} \,dV}$
• ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \psi \nabla \!\varphi \cdot d\mathbf {S} \ =\ \iiint _{V}\left(\psi \nabla ^{2}\!\varphi +\nabla \!\varphi \cdot \nabla \!\psi \right)\,dV}$ (Green's first identity)
• ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \left(\psi \nabla \!\varphi -\varphi \nabla \!\psi \right)\cdot d\mathbf {S} \ =\ }$ ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \left(\psi {\frac {\partial \varphi }{\partial n}}-\varphi {\frac {\partial \psi }{\partial n}}\right)dS}$ ${\displaystyle \displaystyle \ =\ \iiint _{V}\left(\psi \nabla ^{2}\!\varphi -\varphi \nabla ^{2}\!\psi \right)\,dV}$ (Green's second identity)
• ${\displaystyle \iiint _{V}\mathbf {A} \cdot \nabla \psi \,dV\ =\ }$ ${\displaystyle \scriptstyle \partial V}$ ${\displaystyle \psi \mathbf {A} \cdot d\mathbf {S} -\iiint _{V}\psi \nabla \cdot \mathbf {A} \,dV}$ (integration by parts)
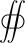
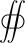
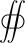
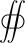
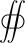
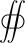
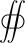
• ${\displaystyle \iiint _{V}\psi \nabla \cdot \mathbf {A} \,dV\ =\ \iint _{\partial V}\psi \mathbf {A} \cdot d\mathbf {S} -\iiint _{V}\nabla \psi \cdot \mathbf {A} \,dV}$ (integration by parts)

Curve–surface integrals

In the following curve–surface integral theorems, S denotes a 2d open surface with a corresponding 1d boundary C = ∂S (a closed curve):

• ${\displaystyle \oint _{\!\!\!\!\partial S}\mathbf {A} \cdot d{\boldsymbol {\ell }}\ =\ \iint _{S}\left(\nabla \times \mathbf {A} \right)\cdot d\mathbf {S} }$ (Stokes' theorem)
• ${\displaystyle \oint _{\!\!\!\!\partial S}\psi \,d{\boldsymbol {\ell }}\ =\ -\iint _{S}\nabla \psi \times d\mathbf {S} }$

Integration around a closed curve in the clockwise sense is the negative of the same line integral in the counterclockwise sense (analogous to interchanging the limits in a definite integral):

${\displaystyle {\scriptstyle \partial S}}$ ${\displaystyle \mathbf {A} \cdot {\rm {d}}{\boldsymbol {\ell }}=-}$ ${\displaystyle {\scriptstyle \partial S}}$ ${\displaystyle \mathbf {A} \cdot {\rm {d}}{\boldsymbol {\ell }}.}$

See also

• Exterior calculus identities
• Exterior derivative
• Del in cylindrical and spherical coordinates
• Vector algebra relations
• Comparison of vector algebra and geometric algebra

References

1. Feynman, R. P.; Leighton, R. B.; Sands, M. (1964). The Feynman Lectures on Physics. Addison-Wesley. Vol II, p. 27–4. ISBN 0-8053-9049-9.
2. Kholmetskii, A. L.; Missevitch, O. V. (2005). "The Faraday induction law in relativity theory" (PDF). p. 4. arXiv:physics/0504223.
3. Doran, C.; Lasenby, A. (2003). Geometric algebra for physicists. Cambridge University Press. p. 169. ISBN 978-0-521-71595-9.
4. Kelly, P. (2013). "Chapter 1.14 Tensor Calculus 1: Tensor Fields" (PDF). Mechanics Lecture Notes Part III: Foundations of Continuum Mechanics. University of Auckland. Retrieved 7 December 2017.

Further reading

• Balanis, Constantine A. (23 May 1989). Advanced Engineering Electromagnetics. ISBN 0-471-62194-3.
• Schey, H. M. (1997). Div Grad Curl and all that: An informal text on vector calculus. W. W. Norton & Company. ISBN 0-393-96997-5.
• Griffiths, David J. (1999). Introduction to Electrodynamics. Prentice Hall. ISBN 0-13-805326-X.