p-value

In null hypothesis significance testing, the p-value[note 1] is the probability of obtaining test results at least as extreme as the results actually observed, under the assumption that the null hypothesis is correct.[2][3] A very small p-value means that such an extreme observed outcome would be very unlikely under the null hypothesis. Reporting p-values of statistical tests is common practice in academic publications of many quantitative fields. Since the precise meaning of p-value is hard to grasp, misuse is widespread and has been a major topic in metascience.[4][5]

Not to be confused with the P-factor.

Basic concepts

In statistics, every conjecture concerning the unknown probability distribution of a collection of random variables representing the observed data ${\displaystyle X}$ in some study is called a statistical hypothesis. If we state one hypothesis only and the aim of the statistical test is to see whether this hypothesis is tenable, but not, at the same time, to investigate other hypotheses, then such a test is called a significance test. Note that the hypothesis might specify the probability distribution of ${\displaystyle X}$ precisely, or it might only specify that it belongs to some class of distributions. Often, we reduce the data to a single numerical statistic ${\displaystyle T}$ whose marginal probability distribution is closely connected to a main question of interest in the study.

A statistical hypothesis that refers only to the numerical values of unknown parameters of the distribution of some statistic is called a parametric hypothesis. A hypothesis which specifies the distribution of the statistic uniquely is called simple, otherwise it is called composite. Methods of verifying statistical hypotheses are called statistical tests. Tests of parametric hypotheses are called parametric tests.[6] We can likewise also have non-parametric hypotheses and non-parametric tests.

The p-value is used in the context of null hypothesis testing in order to quantify the idea of statistical significance of evidence, the evidence being the observed value of the chosen statistic ${\displaystyle T}$.[note 2] Null hypothesis testing is a reductio ad absurdum argument adapted to statistics. In essence, a claim is assumed valid if its counterclaim is highly implausible.

Thus, the only hypothesis that needs to be specified in this test and which embodies the counterclaim is referred to as the null hypothesis; that is, the hypothesis to be nullified. A result is said to be statistically significant if it allows us to reject the null hypothesis. The result, being statistically significant, was highly improbable if the null hypothesis is assumed to be true. A rejection of the null hypothesis implies that the correct hypothesis lies in the logical complement of the null hypothesis. But no specific alternatives need to have been specified. The rejection of the null hypothesis does not tell us which of any possible alternatives might be better supported. However, the user of the test chose the test statistic ${\displaystyle T}$ in the first place probably with particular alternatives in mind; such a test if often used precisely in order to convince people that those alternatives are viable because what was actually observed was extremely unlikely under the null hypothesis.

As a particular example, if a null hypothesis states that a certain summary statistic ${\displaystyle T}$ follows the standard normal distribution N(0,1), then the rejection of this null hypothesis could mean that (i) the mean is not 0, or (ii) the variance is not 1, or (iii) the distribution is not normal. Different tests of the same null hypothesis would be more or less sensitive to different alternatives. Anyway, if we do manage to reject the null hypothesis, even if we know the distribution is normal and variance is 1, the null hypothesis test does not tell us which non-zero values of the mean are now most plausible. If one has a huge amount of independent observations from the same probability distribution, one will eventually be able to show that their mean value is not precisely equal to zero; but the deviation from zero could be so small as to have no practical or scientific interest.

If ${\displaystyle T}$ is a real-valued random variable representing some function of the observed data, to be used as a test-statistic for testing a hypothesis ${\displaystyle H}$ because large values of ${\displaystyle T}$ would seem to discredit the hypothesis, and if it happens to take on the actual value ${\displaystyle t}$, then the p-value of the so called one-sided test of the null-hypothesis ${\displaystyle H}$ based on that test-statistic is the largest value of the probability that ${\displaystyle T}$ could be larger than or equal to ${\displaystyle t}$ if ${\displaystyle H}$ is true.

Definition and interpretation

General

Example of a p-value computation. The vertical coordinate is the probability density of each outcome, computed under the null hypothesis. The p-value is the area under the curve past the observed data point.

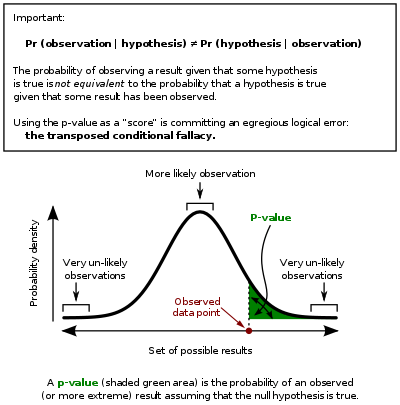
The p-value is defined as the best (largest) probability, under the null hypothesis ${\displaystyle H}$ about the unknown distribution of the test statistic ${\displaystyle T}$, to have observed a value as extreme or more extreme than the value actually observed. If ${\displaystyle t}$ is the observed value, then very often, "as extreme or more extreme than what was actually observed" means ${\displaystyle \{T\geq t\}}$ (right-tail event), but one often also looks at outcomes which are extreme in the other direction, or which are extreme in either direction. If the null hypothesis specifies the probability distribution of the test statistic uniquely, then the p-value is given by

• ${\displaystyle \Pr(T\geq t|H)}$ for a one-sided (right tail) test,
• ${\displaystyle \Pr(T\leq t|H)}$ for a one-sided (left tail) test,
• ${\displaystyle 2\min\{\Pr(T\leq t|H),\Pr(T\geq t|H)\}}$ for a two-sided test,

Notice that just by replacing ${\displaystyle T}$ by ${\displaystyle -T}$ one converts a test based on extremely large values to a test based on extremely small values; and by replacing ${\displaystyle T}$ by ${\displaystyle |T|}$ one gets a test with p-value

• ${\displaystyle \Pr(T\leq -|t||H)+\Pr(T\geq +|t||H)\}.}$

If the null hypothesis allows the test statistic many possible probability distributions, then one works with the worst-case probability, i.e., the one uses the probability distribution under the null hypothesis that is most favourable to the null hypothesis.

If the p-value is very small, then the statistical significance is thought to be very large: under the hypothesis under consideration, something very unlikely has occurred. The investigator who is performing the test probably chose it precisely because they want to discredit the null hypothesis by giving evidence that an alternative explanation of the data should be sought. In a formal significance test, The null hypothesis ${\displaystyle H}$ is rejected if, under the null hypothesis, the probability of such an extreme value (as extreme, or even more extreme) as that which was actually observed is less than or equal to a small, fixed pre-defined threshold value ${\displaystyle \alpha }$, which is referred to as the level of significance. Unlike the p-value, the ${\displaystyle \alpha }$ level is not derived from any observational data and does not depend on the underlying hypothesis; the value of ${\displaystyle \alpha }$ is instead set by the researcher before examining the data. The setting of ${\displaystyle \alpha }$ is arbitrary. By convention, ${\displaystyle \alpha }$ is commonly set to 0.05, 0.01, 0.005, or 0.001.

The p-value is a function of the chosen test statistic ${\displaystyle T}$ and is therefore a random variable in itself. If the null hypothesis fixes the probability distribution of ${\displaystyle T}$ precisely, and if that distribution is continuous, then when the null-hypothesis is true, the p-value is uniformly distributed between 0 and 1, and observing it to take on a value very close to 0 is thought to discredit the hypothesis. Thus, the p-value is not fixed. If the same test is repeated independently with fresh data (always with the same probability distribution), one will find different p-values at every repetition. If the null-hypothesis is composite, or the distribution of the statistic is discrete, the probability of obtaining a p-value less than or equal to any number between 0 and 1 is less than or equal to that number, if the null-hypothesis is true. It remains the case that very small values are very unlikely if the null-hypothesis is true, and that a significance test at level ${\displaystyle \alpha }$ is obtained by rejecting the null-hypothesis if the significance level is less than or equal to ${\displaystyle \alpha }$.

Different p-values based on independent sets of data can be combined, for instance using Fisher's combined probability test.

Distribution

When the null hypothesis is true, if it takes the form ${\displaystyle H_{0}:\theta =\theta _{0}}$, and the underlying random variable is continuous, then the probability distribution of the p-value is uniform on the interval [0,1]. By contrast, if the alternative hypothesis is true, the distribution is dependent on sample size and the true value of the parameter being studied.[7][8]

The distribution of p-values for a group of studies is sometimes called a p-curve.[9] The curve is affected by four factors: the proportion of studies that examined false null hypotheses, the power of the studies that investigated false null hypotheses, the alpha levels, and publication bias.[10] A p-curve can be used to assess the reliability of scientific literature, such as by detecting publication bias or p-hacking.[9][11]

For composite hypothesis

In parametric hypothesis testing problems, a simple or point hypothesis refers to a hypothesis where the parameter's value is assumed to be a single number. In contrast, in a composite hypothesis the parameter's value is given by a set of numbers. For example, when testing the null hypothesis that a distribution is normal with a mean less than or equal to zero against the alternative that the mean is greater than zero (variance known), the null hypothesis does not specify the probability distribution of the appropriate test statistic. In the just mentioned example that would be the Z-statistic belonging to the one-sided one-sample Z-test. For each possible value of the theoretical mean, the Z-test statistic has a different probability distribution. In these circumstances (the case of a so-called composite null hypothesis) the p-value is defined by taking the least favourable null-hypothesis case, which is typically on the border between null and alternative.

Misconceptions

Main article: Misuse of p-values

According to the ASA, there is widespread agreement that p-values are often misused and misinterpreted.[3] One practice that has been particularly criticized is accepting the alternative hypothesis for any p-value nominally less than .05 without other supporting evidence. Although p-values are helpful in assessing how incompatible the data are with a specified statistical model, contextual factors must also be considered, such as "the design of a study, the quality of the measurements, the external evidence for the phenomenon under study, and the validity of assumptions that underlie the data analysis".[3] Another concern is that the p-value is often misunderstood as being the probability that the null hypothesis is true.[3][12] Some statisticians have proposed replacing p-values with alternative measures of evidence,[3] such as confidence intervals,[13][14] likelihood ratios,[15][16] or Bayes factors,[17][18][19] but there is heated debate on the feasibility of these alternatives.[20][21] Others have suggested to remove fixed significance thresholds and to interpret p-values as continuous indices of the strength of evidence against the null hypothesis.[22][23] Yet others suggested to report alongside p-values the prior probability of a real effect that would be required to obtain a false positive risk (i.e. the probability that there is no real effect) below a pre-specified threshold (e.g. 5%).[24]

Usage

The p-value is widely used in statistical hypothesis testing, specifically in null hypothesis significance testing. In this method, as part of experimental design, before performing the experiment, one first chooses a model (the null hypothesis) and a threshold value for p, called the significance level of the test, traditionally 5% or 1%[25] and denoted as α. If the p-value is less than the chosen significance level (α), that suggests that the observed data is sufficiently inconsistent with the null hypothesis and that the null hypothesis may be rejected. However, that does not prove that the tested hypothesis is true. When the p-value is calculated correctly, this test guarantees that the type I error rate is at most α. For typical analysis, using the standard α = 0.05 cutoff, the null hypothesis is rejected when p < .05 and not rejected when p > .05. The p-value does not, in itself, support reasoning about the probabilities of hypotheses but is only a tool for deciding whether to reject the null hypothesis.

Calculation

Usually, ${\displaystyle T}$ is a test statistic, rather than any of the actual observations. A test statistic is the output of a scalar function of all the observations. This statistic provides a single number, such as the average or the correlation coefficient, that summarizes the characteristics of the data, in a way relevant to a particular inquiry. As such, the test statistic follows a distribution determined by the function used to define that test statistic and the distribution of the input observational data.

For the important case in which the data are hypothesized to be a random sample from a normal distribution, depending on the nature of the test statistic and the hypotheses of interest about its distribution, different null hypothesis tests have been developed. Some such tests are the z-test for hypotheses concerning the mean of a normal distribution with known variance, the t-test based on Student's t-distribution of a suitable statistic for hypotheses concerning the mean of a normal distribution when the variance is unknown, the F-test based on the F-distribution of yet another statistic for hypotheses concerning the variance. For data of other nature, for instance categorical (discrete) data, test statistics might be constructed whose null hypothesis distribution is based on normal approximations to appropriate statistics obtained by invoking the central limit theorem for large samples, as in the case of Pearson's chi-squared test.

Thus computing a p-value requires a null hypothesis, a test statistic (together with deciding whether the researcher is performing a one-tailed test or a two-tailed test), and data. Even though computing the test statistic on given data may be easy, computing the sampling distribution under the null hypothesis, and then computing its cumulative distribution function (CDF) is often a difficult problem. Today, this computation is done using statistical software, often via numeric methods (rather than exact formulae), but, in the early and mid 20th century, this was instead done via tables of values, and one interpolated or extrapolated p-values from these discrete values. Rather than using a table of p-values, Fisher instead inverted the CDF, publishing a list of values of the test statistic for given fixed p-values; this corresponds to computing the quantile function (inverse CDF).

Examples

Coin flipping

Main article: Checking whether a coin is fair

As an example of a statistical test, an experiment is performed to determine whether a coin flip is fair (equal chance of landing heads or tails) or unfairly biased (one outcome being more likely than the other).

Suppose that the experimental results show the coin turning up heads 14 times out of 20 total flips. The full data ${\displaystyle X}$ would be a sequence of twenty times the symbol "H" or "T". The statistic on which one might focus, could be the total number ${\displaystyle T}$ of heads. The null hypothesis is that the coin is fair, and coin tosses are independent of one another. If a right-tailed test is considered, which would be the case if one is actually interested in the possibility that the coin is biased towards falling heads, then the p-value of this result is the chance of a fair coin landing on heads at least 14 times out of 20 flips. That probability can be computed from binomial coefficients as

${\displaystyle {\begin{aligned}&\operatorname {Prob} (14{\text{ heads}})+\operatorname {Prob} (15{\text{ heads}})+\cdots +\operatorname {Prob} (20{\text{ heads}})\\&={\frac {1}{2^{20}}}\left[{\binom {20}{14}}+{\binom {20}{15}}+\cdots +{\binom {20}{20}}\right]={\frac {60,\!460}{1,\!048,\!576}}\approx 0.058\end{aligned}}}$

This probability is the p-value, considering only extreme results that favor heads. This is called a one-tailed test. However, one might be interested in deviations in either direction, favoring either heads or tails. The two-tailed p-value, which considers deviations favoring either heads or tails, may instead be calculated. As the binomial distribution is symmetrical for a fair coin, the two-sided p-value is simply twice the above calculated single-sided p-value: the two-sided p-value is 0.115.

In the above example:

• Null hypothesis (H₀): The coin is fair, with Prob(heads) = 0.5
• Test statistic: Number of heads
• Alpha level (designated threshold of significance): 0.05
• Observation O: 14 heads out of 20 flips; and
• Two-tailed p-value of observation O given H₀ = 2*min(Prob(no. of heads ≥ 14 heads), Prob(no. of heads ≤ 14 heads))= 2*min(0.058, 0.978) = 2*0.058 = 0.115.

Note that the Prob (no. of heads ≤ 14 heads) = 1 - Prob(no. of heads ≥ 14 heads) + Prob (no. of head = 14) = 1 - 0.058 + 0.036 = 0.978; however, symmetry of the binomial distribution makes it an unnecessary computation to find the smaller of the two probabilities. Here, the calculated p-value exceeds .05, meaning that the data falls within the range of what would happen 95% of the time were the coin in fact fair. Hence, the null hypothesis is not rejected at the .05 level.

However, had one more head been obtained, the resulting p-value (two-tailed) would have been 0.0414 (4.14%), in which case the null hypothesis would be rejected at the .05 level.

History

John Arbuthnot

Pierre-Simon Laplace

Karl Pearson

Ronald Fisher

Computations of p-values date back to the 1700s, where they were computed for the human sex ratio at birth, and used to compute statistical significance compared to the null hypothesis of equal probability of male and female births.[26] John Arbuthnot studied this question in 1710,[27][28][29][30] and examined birth records in London for each of the 82 years from 1629 to 1710. In every year, the number of males born in London exceeded the number of females. Considering more male or more female births as equally likely, the probability of the observed outcome is 0.5⁸², or about 1 in 4,836,000,000,000,000,000,000,000; in modern terms, the p-value. This is vanishingly small, leading Arbuthnot that this was not due to chance, but to divine providence: "From whence it follows, that it is Art, not Chance, that governs." In modern terms, he rejected the null hypothesis of equally likely male and female births at the p = 1/2⁸² significance level. This and other work by Arbuthnot is credited as "… the first use of significance tests …"[31] the first example of reasoning about statistical significance,[32] and "… perhaps the first published report of a nonparametric test …",[28] specifically the sign test; see details at Sign test § History.

The same question was later addressed by Pierre-Simon Laplace, who instead used a parametric test, modeling the number of male births with a binomial distribution:[33]

In the 1770s Laplace considered the statistics of almost half a million births. The statistics showed an excess of boys compared to girls. He concluded by calculation of a p-value that the excess was a real, but unexplained, effect.

The p-value was first formally introduced by Karl Pearson, in his Pearson's chi-squared test,[34] using the chi-squared distribution and notated as capital P.[34] The p-values for the chi-squared distribution (for various values of χ² and degrees of freedom), now notated as P, was calculated in (Elderton 1902), collected in (Pearson 1914, pp. xxxi–xxxiii, 26–28, Table XII) harv error: no target: CITEREFPearson1914 (help).

The use of the p-value in statistics was popularized by Ronald Fisher,[35] and it plays a central role in his approach to the subject.[36] In his influential book Statistical Methods for Research Workers (1925), Fisher proposed the level p = 0.05, or a 1 in 20 chance of being exceeded by chance, as a limit for statistical significance, and applied this to a normal distribution (as a two-tailed test), thus yielding the rule of two standard deviations (on a normal distribution) for statistical significance (see 68–95–99.7 rule).[37][note 3][38]

He then computed a table of values, similar to Elderton but, importantly, reversed the roles of χ² and p. That is, rather than computing p for different values of χ² (and degrees of freedom n), he computed values of χ² that yield specified p-values, specifically 0.99, 0.98, 0.95, 0,90, 0.80, 0.70, 0.50, 0.30, 0.20, 0.10, 0.05, 0.02, and 0.01.[39] That allowed computed values of χ² to be compared against cutoffs and encouraged the use of p-values (especially 0.05, 0.02, and 0.01) as cutoffs, instead of computing and reporting p-values themselves. The same type of tables were then compiled in (Fisher & Yates 1938), which cemented the approach.[38]

As an illustration of the application of p-values to the design and interpretation of experiments, in his following book The Design of Experiments (1935), Fisher presented the lady tasting tea experiment,[40] which is the archetypal example of the p-value.

To evaluate a lady's claim that she (Muriel Bristol) could distinguish by taste how tea is prepared (first adding the milk to the cup, then the tea, or first tea, then milk), she was sequentially presented with 8 cups: 4 prepared one way, 4 prepared the other, and asked to determine the preparation of each cup (knowing that there were 4 of each). In that case, the null hypothesis was that she had no special ability, the test was Fisher's exact test, and the p-value was ${\displaystyle 1/{\binom {8}{4}}=1/70\approx 0.014,}$ so Fisher was willing to reject the null hypothesis (consider the outcome highly unlikely to be due to chance) if all were classified correctly. (In the actual experiment, Bristol correctly classified all 8 cups.)

Fisher reiterated the p = 0.05 threshold and explained its rationale, stating:[41]

It is usual and convenient for experimenters to take 5 per cent as a standard level of significance, in the sense that they are prepared to ignore all results which fail to reach this standard, and, by this means, to eliminate from further discussion the greater part of the fluctuations which chance causes have introduced into their experimental results.

He also applies this threshold to the design of experiments, noting that had only 6 cups been presented (3 of each), a perfect classification would have only yielded a p-value of ${\displaystyle 1/{\binom {6}{3}}=1/20=0.05,}$ which would not have met this level of significance.[41] Fisher also underlined the interpretation of p, as the long-run proportion of values at least as extreme as the data, assuming the null hypothesis is true.

In later editions, Fisher explicitly contrasted the use of the p-value for statistical inference in science with the Neyman–Pearson method, which he terms "Acceptance Procedures".[42] Fisher emphasizes that while fixed levels such as 5%, 2%, and 1% are convenient, the exact p-value can be used, and the strength of evidence can and will be revised with further experimentation. In contrast, decision procedures require a clear-cut decision, yielding an irreversible action, and the procedure is based on costs of error, which, he argues, are inapplicable to scientific research.

Related quantities

A closely related concept is the E-value,[43] which is the expected number of times in multiple testing that one expects to obtain a test statistic at least as extreme as the one that was actually observed if one assumes that the null hypothesis is true. The E-value is the product of the number of tests and the p-value.

The q-value is the analog of the p-value with respect to the positive false discovery rate.[44] It is used in multiple hypothesis testing to maintain statistical power while minimizing the false positive rate.[45]

See also

• Bonferroni correction
• Counternull
• Fisher's method of combining p-values
• Generalized p-value
• Holm–Bonferroni method
• Multiple comparisons
• p-rep
• p-value fallacy
• Harmonic mean p-value

Notes

1. Italicisation, capitalisation and hyphenation of the term varies. For example, AMA style uses "P value", APA style uses "p value", and the American Statistical Association uses "p-value".[1]
2. The statistical significance of a result does not imply that the result is scientifically significant as well. For instance, a medicine might have a tiny beneficial effect, but it could be so small that it has no medical or scientific interest.
3. To be precise the p = 0.05 corresponds to about 1.96 standard deviations for a normal distribution (two-tailed test), and 2 standard deviations corresponds to about a 1 in 22 chance of being exceeded by chance, or p ≈ 0.045; Fisher notes these approximations.

References

1. http://magazine.amstat.org/wp-content/uploads/STATTKadmin/style%5B1%5D.pdf
2. Aschwanden, Christie (2015-11-24). "Not Even Scientists Can Easily Explain P-values". FiveThirtyEight. Archived from the original on 25 September 2019. Retrieved 11 October 2019.
3. Wasserstein, Ronald L.; Lazar, Nicole A. (7 March 2016). "The ASA's Statement on p-Values: Context, Process, and Purpose". The American Statistician. 70 (2): 129–133. doi:10.1080/00031305.2016.1154108.
4. Hubbard, Raymond; Lindsay, R. Murray (2008). "Why P Values Are Not a Useful Measure of Evidence in Statistical Significance Testing". Theory & Psychology. 18 (1): 69–88. doi:10.1177/0959354307086923.
5. Ioannidis, John P. A.; et al. (January 2017). "A manifesto for reproducible science" (PDF). Nature Human Behaviour. 1: 0021. doi:10.1038/s41562-016-0021. S2CID 6326747.
6. Fisz, Marek (1963). "Significance Testing". Probability theory and mathematical statistics (3 ed.). New York: John Wiley and Sons, Inc. p. 425.
7. Bhattacharya, Bhaskar; Habtzghi, DeSale (2002). "Median of the p value under the alternative hypothesis". The American Statistician. 56 (3): 202–6. doi:10.1198/000313002146. S2CID 33812107.
8. Hung, H.M.J.; O'Neill, R.T.; Bauer, P.; Kohne, K. (1997). "The behavior of the p-value when the alternative hypothesis is true". Biometrics (Submitted manuscript). 53 (1): 11–22. doi:10.2307/2533093. JSTOR 2533093. PMID 9147587.
9. Head ML, Holman L, Lanfear R, Kahn AT, Jennions MD (2015). "The extent and consequences of p-hacking in science". PLOS Biol. 13 (3): e1002106. doi:10.1371/journal.pbio.1002106. PMC 4359000. PMID 25768323.
10. Lakens D (2015). "What p-hacking really looks like: a comment on Masicampo and LaLande (2012)". Q J Exp Psychol (Hove). 68 (4): 829–32. doi:10.1080/17470218.2014.982664. PMID 25484109.
11. Simonsohn U, Nelson LD, Simmons JP (2014). "p-Curve and Effect Size: Correcting for Publication Bias Using Only Significant Results". Perspect Psychol Sci. 9 (6): 666–81. doi:10.1177/1745691614553988. PMID 26186117. S2CID 39975518.
12. Colquhoun, David (2014). "An investigation of the false discovery rate and the misinterpretation of p-values". Royal Society Open Science. 1 (3): 140216. arXiv:1407.5296. Bibcode:2014RSOS....140216C. doi:10.1098/rsos.140216. PMC 4448847. PMID 26064558.
13. Lee, Dong Kyu (7 March 2017). "Alternatives to P value: confidence interval and effect size". Korean Journal of Anesthesiology. 69 (6): 555–562. doi:10.4097/kjae.2016.69.6.555. ISSN 2005-6419. PMC 5133225. PMID 27924194.
14. Ranstam, J. (August 2012). "Why the P-value culture is bad and confidence intervals a better alternative" (PDF). Osteoarthritis and Cartilage. 20 (8): 805–808. doi:10.1016/j.joca.2012.04.001. PMID 22503814.
15. Perneger, Thomas V. (12 May 2001). "Sifting the evidence: Likelihood ratios are alternatives to P values". BMJ: British Medical Journal. 322 (7295): 1184–5. doi:10.1136/bmj.322.7295.1184. ISSN 0959-8138. PMC 1120301. PMID 11379590.
16. Royall, Richard (2004). "The Likelihood Paradigm for Statistical Evidence". The Nature of Scientific Evidence. pp. 119–152. doi:10.7208/chicago/9780226789583.003.0005. ISBN 9780226789576.
17. Schimmack, Ulrich (30 April 2015). "Replacing p-values with Bayes-Factors: A Miracle Cure for the Replicability Crisis in Psychological Science". Replicability-Index. Retrieved 7 March 2017.
18. Marden, John I. (December 2000). "Hypothesis Testing: From p Values to Bayes Factors". Journal of the American Statistical Association. 95 (452): 1316–1320. doi:10.2307/2669779. JSTOR 2669779.
19. Stern, Hal S. (16 February 2016). "A Test by Any Other Name: Values, Bayes Factors, and Statistical Inference". Multivariate Behavioral Research. 51 (1): 23–29. doi:10.1080/00273171.2015.1099032. PMC 4809350. PMID 26881954.
20. Murtaugh, Paul A. (March 2014). "In defense of p-values". Ecology. 95 (3): 611–617. doi:10.1890/13-0590.1. PMID 24804441.
21. Aschwanden, Christie (Mar 7, 2016). "Statisticians Found One Thing They Can Agree On: It's Time To Stop Misusing P-Values". FiveThirtyEight.
22. Amrhein, Valentin; Korner-Nievergelt, Fränzi; Roth, Tobias (2017). "The earth is flat (p > 0.05): significance thresholds and the crisis of unreplicable research". PeerJ. 5: e3544. doi:10.7717/peerj.3544. PMC 5502092. PMID 28698825.
23. Amrhein, Valentin; Greenland, Sander (2017). "Remove, rather than redefine, statistical significance". Nature Human Behaviour. 2 (1): 0224. doi:10.1038/s41562-017-0224-0. PMID 30980046. S2CID 46814177.
24. Colquhoun D (December 2017). "p-values". Royal Society Open Science. 4 (12): 171085. doi:10.1098/rsos.171085. PMC 5750014. PMID 29308247.
25. Nuzzo, R. (2014). "Scientific method: Statistical errors". Nature. 506 (7487): 150–152. Bibcode:2014Natur.506..150N. doi:10.1038/506150a. PMID 24522584.
26. Brian, Éric; Jaisson, Marie (2007). "Physico-Theology and Mathematics (1710–1794)". The Descent of Human Sex Ratio at Birth. Springer Science & Business Media. pp. 1–25. ISBN 978-1-4020-6036-6.
27. John Arbuthnot (1710). "An argument for Divine Providence, taken from the constant regularity observed in the births of both sexes" (PDF). Philosophical Transactions of the Royal Society of London. 27 (325–336): 186–190. doi:10.1098/rstl.1710.0011. S2CID 186209819.
28. Conover, W.J. (1999), "Chapter 3.4: The Sign Test", Practical Nonparametric Statistics (Third ed.), Wiley, pp. 157–176, ISBN 978-0-471-16068-7
29. Sprent, P. (1989), Applied Nonparametric Statistical Methods (Second ed.), Chapman & Hall, ISBN 978-0-412-44980-2
30. Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. pp. 225–226. ISBN 978-0-67440341-3.
31. Bellhouse, P. (2001), "John Arbuthnot", in Statisticians of the Centuries by C.C. Heyde and E. Seneta, Springer, pp. 39–42, ISBN 978-0-387-95329-8
32. Hald, Anders (1998), "Chapter 4. Chance or Design: Tests of Significance", A History of Mathematical Statistics from 1750 to 1930, Wiley, p. 65
33. Stigler, Stephen M. (1986). The History of Statistics: The Measurement of Uncertainty Before 1900. Harvard University Press. p. 134. ISBN 978-0-67440341-3.
34. Pearson, Karl (1900). "On the criterion that a given system of deviations from the probable in the case of a correlated system of variables is such that it can be reasonably supposed to have arisen from random sampling" (PDF). Philosophical Magazine. Series 5. 50 (302): 157–175. doi:10.1080/14786440009463897.
35. Inman 2004. sfn error: no target: CITEREFInman2004 (help)
36. Hubbard, Raymond; Bayarri, M. J. (2003), "Confusion Over Measures of Evidence (p′s) Versus Errors (α′s) in Classical Statistical Testing", The American Statistician, 57 (3): 171–178 [p. 171], doi:10.1198/0003130031856
37. Fisher 1925, p. 47, Chapter III. Distributions.
38. Dallal 2012, Note 31: Why P=0.05?.
39. Fisher 1925, pp. 78–79, 98, Chapter IV. Tests of Goodness of Fit, Independence and Homogeneity; with Table of χ², Table III. Table of χ².
40. Fisher 1971, II. The Principles of Experimentation, Illustrated by a Psycho-physical Experiment.
41. Fisher 1971, Section 7. The Test of Significance.
42. Fisher 1971, Section 12.1 Scientific Inference and Acceptance Procedures.
43. National Institutes of Health definition of E-value
44. Storey, John D (2003). "The positive false discovery rate: a Bayesian interpretation and the q-value". The Annals of Statistics. 31 (6): 2013–2035. doi:10.1214/aos/1074290335.
45. Storey, John D; Tibshirani, Robert (2003). "Statistical significance for genomewide studies". PNAS. 100 (16): 9440–9445. Bibcode:2003PNAS..100.9440S. doi:10.1073/pnas.1530509100. PMC 170937. PMID 12883005.

Further reading

• Lydia Denworth, "A Significant Problem: Standard scientific methods are under fire. Will anything change?", Scientific American, vol. 321, no. 4 (October 2019), pp. 62–67. "The use of p values for nearly a century [since 1925] to determine statistical significance of experimental results has contributed to an illusion of certainty and [to] reproducibility crises in many scientific fields. There is growing determination to reform statistical analysis... Some [researchers] suggest changing statistical methods, whereas others would do away with a threshold for defining "significant" results." (p. 63.)
• Elderton, William Palin (1902). "Tables for Testing the Goodness of Fit of Theory to Observation". Biometrika. 1 (2): 155–163. doi:10.1093/biomet/1.2.155.
• Fisher, Ronald (1925). Statistical Methods for Research Workers. Edinburgh, Scotland: Oliver & Boyd. ISBN 978-0-05-002170-5.
• Fisher, Ronald A. (1971) [1935]. The Design of Experiments (9th ed.). Macmillan. ISBN 978-0-02-844690-5.
• Fisher, R. A.; Yates, F. (1938). Statistical tables for biological, agricultural and medical research. London, England.
• Stigler, Stephen M. (1986). The history of statistics : the measurement of uncertainty before 1900. Cambridge, Mass: Belknap Press of Harvard University Press. ISBN 978-0-674-40340-6.
• Hubbard, Raymond; Armstrong, J. Scott (2006). "Why We Don't Really Know What Statistical Significance Means: Implications for Educators" (PDF). Journal of Marketing Education. 28 (2): 114–120. doi:10.1177/0273475306288399. hdl:2092/413. Archived from the original on May 18, 2006.CS1 maint: unfit url (link)
• Hubbard, Raymond; Lindsay, R. Murray (2008). "Why P Values Are Not a Useful Measure of Evidence in Statistical Significance Testing" (PDF). Theory & Psychology. 18 (1): 69–88. doi:10.1177/0959354307086923. Archived from the original (PDF) on 2016-10-21. Retrieved 2015-08-28.
• Stigler, S. (December 2008). "Fisher and the 5% level". Chance. 21 (4): 12. doi:10.1007/s00144-008-0033-3.
• Dallal, Gerard E. (2012). The Little Handbook of Statistical Practice.
• Biau, D.J.; Jolles, B.M.; Porcher, R. (March 2010). "P value and the theory of hypothesis testing: an explanation for new researchers". Clin Orthop Relat Res. 463 (3): 885–892. doi:10.1007/s11999-009-1164-4. PMC 2816758. PMID 19921345.
• Reinhart, Alex (2015). Statistics Done Wrong: The Woefully Complete Guide. No Starch Press. p. 176. ISBN 978-1593276201.

External links

• Free online p-values calculators for various specific tests (chi-square, Fisher's F-test, etc.).
• Understanding p-values, including a Java applet that illustrates how the numerical values of p-values can give quite misleading impressions about the truth or falsity of the hypothesis under test.
• StatQuest: P Values, clearly explained on YouTube
• StatQuest: P-value pitfalls and power calculations on YouTube