Dihedron

A dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is the fundamental domain of a lens space L(p,q).[1] Dihedra have also been called bihedra,[2] flat polyhedra,[3] or doubly covered polygons.[3]

Set of regular n-gonal dihedra
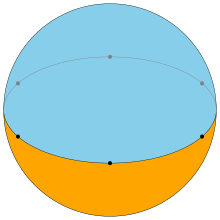Example hexagonal dihedron on a sphere
Type	Regular polyhedron or spherical tiling
Faces	2 n-gons
Edges	n
Vertices	n
Vertex configuration	n.n
Wythoff symbol	2 | n 2
Schläfli symbol	{n,2}
Coxeter diagram
Symmetry group	Dnh, [2,n], (*22n), order 4n
Rotation group	Dn, [2,n]^+, (22n), order 2n
Dual polyhedron	hosohedron

A regular dihedron is the dihedron formed by two regular polygons, which may be described by the Schläfli symbol {n,2}.[4] As a spherical polyhedron, each polygon of such a dihedron fills a hemisphere, with a regular n-gon on a great circle equator between them.

The dual of a n-gonal dihedron is the n-gonal hosohedron, where n digon faces share two vertices.

As a polyhedron

A dihedron can be considered a degenerate prism consisting of two (planar) n-sided polygons connected "back-to-back", so that the resulting object has no depth. The polygons must be congruent, but glued in such a way that one is the mirror image of the other.

Dihedra can arise from Alexandrov's uniqueness theorem, which characterizes the distances on the surface of any convex polyhedron as being locally Euclidean except at a finite number of points with positive angular defect summing to 4π. This characterization holds also for the distances on the surface of a dihedron, so the statement of Alexandrov's theorem requires that dihedra be considered to be convex polyhedra.[5]

As a tiling on a sphere

As a spherical tiling, a dihedron can exist as nondegenerate form, with two n-sided faces covering the sphere, each face being a hemisphere, and vertices around a great circle. (It is regular if the vertices are equally spaced.)

The regular polyhedron {2,2} is self-dual, and is both a hosohedron and a dihedron.

Regular dihedra: (spherical tilings)

Image
Schläfli	{2,2}	{3,2}	{4,2}	{5,2}	{6,2}...
Coxeter
Faces	2 {2}	2 {3}	2 {4}	2 {5}	2 {6}
Edges and vertices	2	3	4	5	6

Apeirogonal dihedron

In the limit the dihedron becomes an apeirogonal dihedron as a 2-dimensional tessellation:

Ditopes

A regular ditope is an n-dimensional analogue of a dihedron, with Schläfli symbol {p,...q,r,2}. It has two facets, {p,...q,r}, which share all ridges, {p,...q} in common.[6]

See also

• Polyhedron
• Polytope

References

1. Gausmann, Evelise; Roland Lehoucq; Jean-Pierre Luminet; Jean-Philippe Uzan; Jeffrey Weeks (2001). "Topological Lensing in Spherical Spaces". Classical and Quantum Gravity. 18: 5155–5186. arXiv:gr-qc/0106033. Bibcode:2001CQGra..18.5155G. doi:10.1088/0264-9381/18/23/311.
2. Kántor, S. (2003), "On the volume of unbounded polyhedra in the hyperbolic space" (PDF), Beiträge zur Algebra und Geometrie, 44 (1): 145–154, MR 1990989.
3. O'Rourke, Joseph (2010), Flat zipper-unfolding pairs for Platonic solids, arXiv:1010.2450, Bibcode:2010arXiv1010.2450O
4. Coxeter, H. S. M., Regular Polytopes (3rd ed.), Dover Publications Inc., p. 12, ISBN 0-486-61480-8
5. O'Rourke, Joseph (2010), On flat polyhedra deriving from Alexandrov's theorem, arXiv:1007.2016, Bibcode:2010arXiv1007.2016O
6. McMullen, Peter; Schulte, Egon (December 2002), Abstract Regular Polytopes (1st ed.), Cambridge University Press, p. 158, ISBN 0-521-81496-0

External links

• Weisstein, Eric W. "Dihedron". MathWorld.