Enneahedron
In geometry, an enneahedron (or nonahedron) is a polyhedron with nine faces. There are 2606 types of convex enneahedron, each having a different pattern of vertex, edge, and face connections.[1] None of them are regular.
Examples
The most familiar enneahedra are the octagonal pyramid and the heptagonal prism. The heptagonal prism is a uniform polyhedron, with two regular heptagon faces and seven square faces. The octagonal pyramid has eight isosceles triangular faces around a regular octagonal base. Two more enneahedra are also found among the Johnson solids: the elongated square pyramid and the elongated triangular bipyramid. The three-dimensional associahedron, a near-miss Johnson solid with six pentagonal faces and three quadrilateral faces, is an enneahedron. Five Johnson solids have enneahedral duals: the triangular cupola, gyroelongated square pyramid, self-dual elongated square pyramid, triaugmented triangular prism (whose dual is the associahedron), and tridiminished icosahedron. Another enneahedron is the diminished trapezohedron with a square base, and 4 kite and 4 triangle faces.
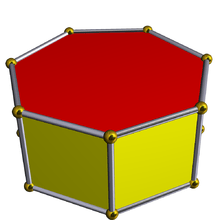 Heptagonal prism |
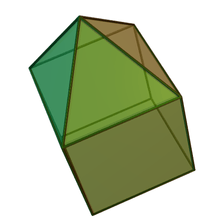 Elongated square pyramid |
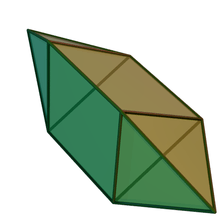 Elongated triangular bipyramid |
 Dual of triangular cupola |
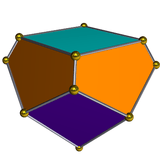 Dual of gyroelongated square pyramid |
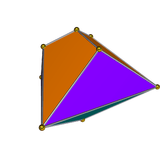 Dual of tridiminished icosahedron |
 Square diminished trapezohedron |
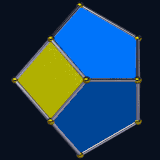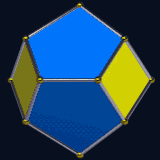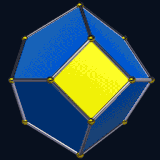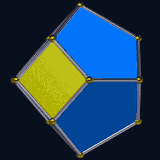 Truncated triangular bipyramid, near-miss Johnson solid, and associahedron. |
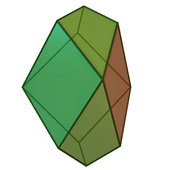 Herschel enneahedron |
The Herschel graph represents the vertices and edges of the Herschel enneahedron above, with all of its faces quadrilaterals. It is the simplest polyhedron without a Hamiltonian cycle, the only enneahedron in which all faces have the same number of edges, and one of only three bipartite enneahedra.
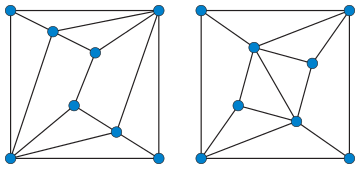
The smallest pair of isospectral polyhedral graphs are enneahedra with eight vertices each.[2]
Space-filling enneahedra

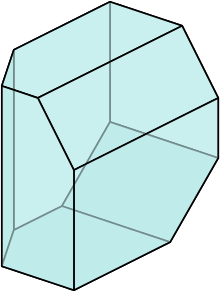
Slicing a rhombic dodecahedron in half through the long diagonals of four of its faces results in a self-dual enneahedron, the square diminished trapezohedron, with one large square face, four rhombus faces, and four isosceles triangle faces. Like the rhombic dodecahedron itself, this shape can be used to tessellate three-dimensional space.[3] An elongated form of this shape that still tiles space can be seen atop the rear side towers of the 12th-century Romanesque Basilica of Our Lady (Maastricht). The towers themselves, with their four pentagonal sides, four roof facets, and square base, form another space-filling enneahedron.
More generally, Goldberg (1982) found at least 40 topologically distinct space-filling enneahedra.[4]
Topologically distinct enneahedra
There are 2606 topologically distinct convex enneahedra, excluding mirror images. These can be divided into subsets of 8, 74, 296, 633, 768, 558, 219, 50, with 7 to 14 vertices respectively.[5] A table of these numbers, together with a detailed description of the nine-vertex enneahedra, was first published in the 1870s by Thomas Kirkman.[6]
References
- Steven Dutch: How Many Polyhedra are There? Archived 2010-06-07 at the Wayback Machine
- Hosoya, Haruo; Nagashima, Umpei; Hyugaji, Sachiko (1994), "Topological twin graphs. Smallest pair of isospectral polyhedral graphs with eight vertices", Journal of Chemical Information and Modeling, 34 (2): 428–431, doi:10.1021/ci00018a033.
- Critchlow, Keith (1970), Order in space: a design source book, Viking Press, p. 54.
- Goldberg, Michael (1982), "On the space-filling enneahedra", Geometriae Dedicata, 12 (3): 297–306, doi:10.1007/BF00147314.
- Counting polyhedra
- Biggs, N.L. (1981), "T.P. Kirkman, mathematician", The Bulletin of the London Mathematical Society, 13 (2): 97–120, doi:10.1112/blms/13.2.97, MR 0608093.
External links
- Enumeration of Polyhedra by Steven Dutch
- Weisstein, Eric W. "Nonahedron". MathWorld.